Моделирование кинетики химических реакций методом второго порядка для неявных систем
Автор: Кнауб Л.В., Новиков А.Е., Новиков Е.А.
Журнал: Вестник Красноярского государственного аграрного университета @vestnik-kgau
Рубрика: Математика
Статья в выпуске: 10, 2014 года.
Бесплатный доступ
Построен двухстадийный L-устойчивый метод второго порядка для решения неявных систем. Метод отличается от классических схем приближенным нахождением производной решения. Приведены результаты численного моделирования кинетики химической реакции.
Дифференциально-алгебраическая задача, метод типа розенброка, химическая кинетика
Короткий адрес: https://sciup.org/14084952
IDR: 14084952 | УДК: 519.622
Текст научной статьи Моделирование кинетики химических реакций методом второго порядка для неявных систем
F ( x , x ', t ) = 0 , x ( 1 0) = x 0 , 1 0 < t < t k ,
где x и F – вещественные N -мерные вектор-функции; t – независимая переменная. Современные численные методы обычно предполагают задание явной зависимости производной [1–2], то есть
x' = f (t, x), x (10) = x0
t 0 < t < t k ■
Приведение задачи (1) к виду (2) требует дополнительных затрат на шаг интегрирования, которые связаны с обращением матрицы Fy. Разрешенная задача (2) жесткая, что приводит к необходимости применения L-устойчивых методов, которые нуждаются в обращении матрицы Якоби. Наиболее известные алгоритмы решения задачи (1) основаны на многошаговых численных формулах [3]. Однако многие практические задачи описываются жесткими непрерывно-дискретными системами, которые в современной литературе называют гибридными задачами [4]. Для них характерным является непрерывное описание режимов, смена которых происходит дискретно. В такой ситуации многошаговые методы могут быть малоэффективны. При решении жестких задач широкое распространение получили методы типа Розенброка [5]. Здесь построен двухстадийный L-устойчивый метод второго порядка точности решения неявных задач. Метод отли- чается от классических схем типа Розенброка приближенным нахождением производной решения. Приведены результаты численного моделирования кинетики химической реакции.
Численная схема. Используя обозначение x'=y, задачу (1) можно переписать в виде системы дифференциально-алгебраических уравнений x ' = y, F (x, y, t) = 0, t о < t < tk.
с начальными условиями x ( t о )= x о и y ( t о )= у о . Дополнительное условие y ( t о )= у о можно вычислить, например, решая задачу F ( x о , у , t о )=0 методом установления [6]. Ниже будем предполагать существование и единственность решения задачи (3) и невырожденность матрицы D n = F ny + ahF nX , где a - числовой коэффициент, h - шаг интегрирования, а F ny и F nX - частные производные функции F ( x , у , t ), вычисленные в точке t n . Тогда m -стадийный метод типа Розенброка для численного решения задачи (3) имеет вид [6]
m
m
x n + 1 = x n + Е Pk x • У п + 1 = У п + Е Р к •
i = 1
i = 1
Dk = hF,y.' У,, + Евук,У — ah2F j=1 7
i - 1
i - 1
hF x , + Е в у к x , У п + Е в к , t n + h - Z в 9
j = 1 7
i - 1
i ah
kx
h • у,+Е в ky i j=1
где a , p i , P ij - числовые коэффициенты. При применении численных формул (4) для решения задачи (2) получим классические методы типа Розенброка [5]. Так как у о вычисляется приближенно, будем предполагать выполненным соотношение || F ( x о , у о , t о )|| < Ch p , где || - 1| - некоторая норма в R N , C - константа, не зависящая от величины шага интегрирования, p - порядок точности метода.
Для решения (3) рассмотрим формулу типа Розенброка вида xn+1 = xn + P1 k1 + Р2 k2x • Уп+1 = Уп + P1 k1У + P 2 k2У •
Dk = h [F„ - Уп — alF - F (xn,у,, t,)], k = a-l (kx - Ну, ) / h, (5) D,kx = hF„ ■(Уп + в2,kУ)-ah2F. -hFn(x, + в21 k,yn + в2,F,tn + в21 h), k7 = a
k x - h ( У , + в 21 k" ) ] / h .
Разложим стадии k ix и k iy в ряды Тейлора по степеням h и подставим в первую формулу (5). Сравнивая полученное представление приближенного решения с рядом Тейлора для точного решения, получим условия второго порядка точности схемы (5)
Р 1 + Р 2 = 1 , в 21 Р 2 = 0.5 - fl ■
Разлагая F n +i = F ( x n +i , у п +i , t n +i ) в ряд Тейлора с учетом (6), получим
F n + i = a - 2 ( a 2 - 2 a + 0.5 ) F + O ( h 2 ) .
Условие F n +i =O( h 2) приводит к уравнению a 2-2 a +0.5=0. Данное соотношение обеспечивает L - устойчивость схемы (5) при решении разрешенной задачи. Уравнение a 2-2 a +0,5=0 имеет два вещественных корня. Из численных экспериментов следует, что корень a=1-0,5 ^ 2 предпочтительнее, потому что он приводит к более эффективным расчетам. Требование L -устойчивости промежуточной численной формулы приводит к соотношению ^ 21 = a . В результате получим коэффициенты L -устойчивого метода (5) второго порядка
P i = в 2i = а = 1 - 0.542 , p 2 = 1 - а = 0.5-42 .
Контроль точности. Неравенство для контроля точности построим по аналогии [6-8], то есть на каждом шаге следует проверять неравенство
II k2 - К II< е, где к i x и к 2 x заданы при описании численной схемы (5), s - требуемая точность расчетов, где || -1| - некоторая норма в RN. В расчетах использовалась норма max
1 < i < N
। g i । ; . 1 x n 1 + r
где r - положительное число. Если | y n |< r , то по i -й компоненте решения контролируется абсолютная ошибка rε ; в противном случае контролируется относительная ошибка ε . В отличие от методов типа Розенброка решения разрешенных систем производная в численной формуле (5) вычисляется приближенно, и поэтому при выборе шага дополнительно проверяется неравенство || D n -1 F n || <е .
Тестовый пример. Задача взята из [9], схема реакции имеет вид
2FLB+1CO, --FLBT+H2O . ZLA+FLB < < / K > FLBT+ZHU -
2 2 2 4 k 2
FLB+ZHU < - FLB .ZHU .
где к есть константа скоростей стадий. Последнее уравнение реакции описывает равновесие. Значение K s вычисляется по формуле
Приток углекислого газа на единицу объема обозначается через Fin, где klA - коэффициент массопе-реноса, H - константа Генри и p(CO2) - парциальное давление углекислого газа. В расчетах значение дав- ления p(CO2) предполагается независимым от углекислого газа [CO2], причем k1=18,7, k2=0,58, k3=0,09, k4=0,42, K=34,4, klA=3,3, Ks=115,83, H=737 и p(CO2) =0,9.
Процесс начинается путем смешивания 0,444 моль/литр реагента FLB с 0,007 моль/литр элемента ZHU. В начальный момент времени концентрация углекислого газа полагается равным 0,00123 моль/литр. По переменной у 6 начальное условие задается формулой у 0,6 = K s • y 0,1 * у 0,4 . По остальным компонентам начальные условия равны нулю. Теперь, вводя обозначения концентраций реагентов по формулам y 1 =[FLB], у 2 =[CO 2 ], у 3 =[FLBT], у 4 =[ZHU], у 5 = [ ZLA ] и у 6 =[FLB.ZHU], получим систему уравнений вида
Му' = f ( у ) , у ( 0 ) = у 0 , у '( 0 ) = у ‘ , у £ R 6 , 0 < t < 180 . (6)
Ранг матрицы M равен пяти и она имеет вид
< 1 0 0 0 0 0 Л
М =
0 0 0 0 1 0
ч 0 0 0 0 0 0 ;
Функция f ( y ) записывается следующим образом:
f 1 = - 2 r + r 2 - r3 - r , f 2 = - 0.5 r - r4 - 0.5 r + F in , f 3 = r - r + r , f 4 =- r 2 + r 3 - 2 r 4 , f 5 = r 2 - r 3 + r 5 , f 6 = Ks * у 1 * у 4 - у 6 •
Значения переменных r i , 1 < i < 5 , и Fin задаются формулами:
rl = ki • у4 • У^2 , r2 = k2 • у3 • у4 , r3 = 7 k2 • у1 • у5 , K r4 = k3 * у1 * у42 , r5 = k4 * у62 * у22 , Fin = klA *[ p (CO2)/H - у 2 ].
Начальные условия имеют вид у0 =(0.444, 0.00123, 0., 0.007, 0., Ks ■ уw • ум)T, у0 = f (у0).
Результаты расчетов. Расчеты проводились на PC Intel(R) Core(TM) i7-3770S CPU@3.10GHz с двойной точностью. Задаваемая точность £ расчетов полагалась равной 10-2. Моделирование выполняется на интервале времени [0,180]. Решение в конце интервала интегрирования имеет вид у1 = 0.115, у 2 = 0.120 *10-2, у 3 = 0.161, у4 = 0.366 *10-3, у 5 = 0.171 * 10-1, у6 = 0.487 *10-2.
Зависимость концентрации CO 2 от времени приведена на рисунке.
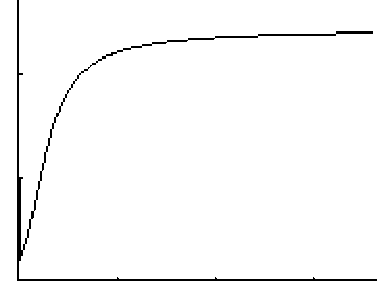
Зависимость концентрации CO 2 от времени
Заключение. Из результатов сравнения построенного алгоритма интегрирования с методом типа Ро-зенброка для разрешенных задач следует, что эффективности алгоритмов отличаются незначительно. Отсюда можно сделать вывод, что построенный алгоритм можно применять для решения как разрешенных, так и неразрешенных относительно производной задач.


