Моделирование кодовых последовательностей с энтропией естественных и искусственных биометрических языков

Задача моделирования естественных и искусственных языков возникает во многих практических приложениях. Традиционно этим занимались криптоаналитики и лингвисты [1-2]. Новым направлением науки, использующим языковые модели, является биометрия [3]. Высоконадежные нейросетевые преобразователи биометрия-код, выполненные по требованиям отечественного стандарта [4], при их тестировании ведут себя как источники некоторого биометрического языка, порождая сильно связанные между собой кодовые последовательности. Естественно, что эти последовательности можно исследовать через вычисление их энтропии и плотности распределения значений парных коэффициентов корреляции [5-6]. При исследовании влияния многомерных статистик той или иной кодовой последовательности на ее функцию энтропии необходимо уметь моделировать эти кодовые последовательности с разными уровнями корреляционных связей.

Генерирование случайных кодов с равномерной корреляционной матрицей

Примитивным решением задачи является пренебрежение корреляционными связями. В этом случае для генерирования случайных кодов можно использовать достаточное число независимых генераторов случайного «белого» шума. Пойдем на заведомую избыточность описания и будем считать, что система из n независимых случайных генераторов данных х_i,j порождается путем псевдоумножения вектора их данных на единичную корреляционную матрицу в соответствии с формулой (1).

Очевидно, что псевдоумножение на единичную матрицу ничего не дает, и данные на выходе останутся независимыми. Корреляционная матрица выходной последовательности кодов оказывается единичной.

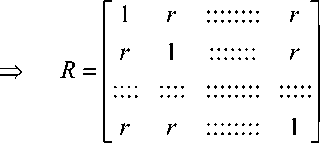
Легко показать, что если нули в матрице формулы (1) заменить на некоторое постоян- ное число а < 1, то входные и выходные данные системы будут существенно различаться. Входные данные останутся независимыми, а выходные данные будут зависимыми. При этом все коэффициенты, находящиеся вне корреляционной матрицы, оказываются одинаковыми (2).

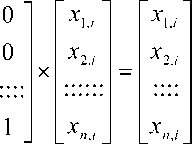
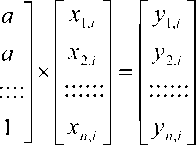
Номограмма зависимости значения параметра а связывающей матрицы от значения параметра r корреляционных матриц размерностью 2; 4; 8; 16; 32; 64; 128 и 256 приведена на рис. 1.

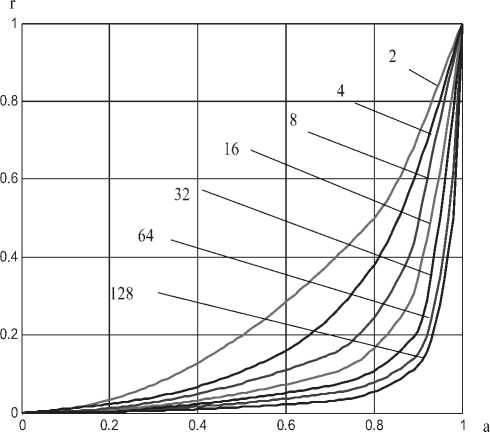
Рис. 1. Номограмма связи параметров a и r для разных размерностей генераторов зависимых данных

Из рис. 1 видно, что с повышением размерности задачи моделирования зависимость параметра а связывающей матрицы с коэффициентами корреляции становится все более и более нелинейной. По мере роста размерности задачи кривая связи r ( a ) все более и более сильно прижимается к горизонтальной и вертикальной осям координат.

Генерирование случайных кодов, воспроизводящих статистики синтетических языков преобразователей биометрия-код

Генерирование кодов с равномерной корреляционной матрицей плохо отражает реальные данные биометрических кодов. В связи с этим для большей реалистичности данных необходимо выбирать коэффициенты а случайными, причем желательно использовать два случайных генератора нормальных данных с одинаковыми среднеквадратическими отклонениями и симметричными математическими ожиданиями а и - а . Пример распределения значений подобных генераторов приведен на рис. 2.

При моделировании зависимых выходных кодов биометрических преобразователей связывающая матрица может быть как симметричной, так и асимметричной. Естественно, что более удобными для моделирования являются симметричные связывающие матрицы. Они формируются путем случайного выбора данных двух генераторов и подстановки этих данных в верхнюю часть матрицы, далее нижняя часть матрицы заполняется зеркальным отражением верхней части матрицы.

Пример распределения значений парных коэффициентов корреляции, соответствующий распределению значений симметричной связывающей матрицы, полученных от генераторов случайных данных с распределениями, показанными на рис. 2, приводится на рис. 3.

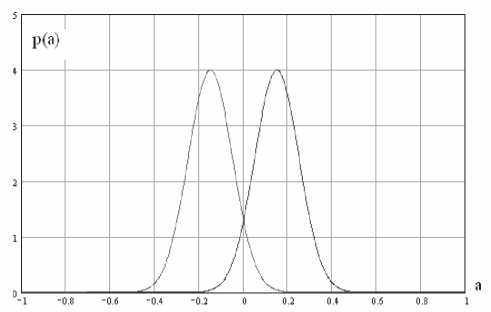
Рис. 2. Пример распределения значений двух генераторов случайных значений параметра а и -а , позволяющих получать случайные значения элементов связывающей данные матрицы

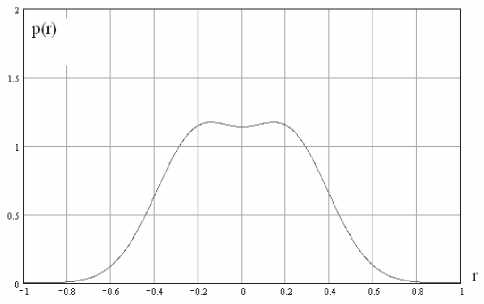
Рис. 3. Распределение значений парных коэффициентов корреляции, полученное при использовании данных двух симметричных генераторов параметра а связывающей матрицы

Предложенный выше подход к имитации биометрических кодов конструктивен, так как позволяет добиваться любых распределений парных коэффициентов корреляции воспроизводимой кодовой последовательности, подбирая (регулируя) всего два параметра двух генераторов (их математическое ожидание и среднеквадратическое отклонение). Если пытаться решить туже самую задачу, пользуясь классическим подходом Шалыгина [7], то решить задачу для матриц высокой размерности не удается. Предлагаемый подход позволяет решать задачу для матриц очень высокой размерности: 32; 64; 128; 256; 512 и 1024. При этом значительных вычислительных затрат не требуется, а задача вычисления высокоразмерной матрицы параметров моделирования оказывается устойчивой.

Описанный выше подход к моделированию разработан с ориентацией на имитацию искусственных биометрических языков, являющихся откликами обученных нейросетевых преобразователей биометрия-код, выполненных по требованиям ГОСТ Р 52633-2006. Именно для этого класса устройств характерны матрицы корреляционных парных связей, имеющих случайный характер (параметры соответствующей корреляционной матрицы вне ее диагонали случайны).

Генерация кодов, воспроизводящих энтропию и корреляции естественных языков

Необходимо отметить, что описанный выше подход к моделированию кодовых последовательностей неприменим к естественным языкам (например, русскому языку или английскому языку). Проведенные исследования показали, что для естественных языков характерны корреляционные матрицы взаимосвязи со случайными знаками коэффициентов парной корреляции и далеко не случайным значением их модулей. Все естественные языки имеют модули коэффициентов корреляции, монотонно убывающие по мере удаления положения коэффициента от диагонали корреляционной матрицы. В связи с тем, что модули коэффициентов корреляции связаны монотонными функциями с параметрами а (см. рис. 1), модули параметров связывающей матрицы будут также уменьшаться по мере удаления их от диагонали связывающей матрицы а в формуле (2).

Очевидно, что рассчитать модули корреляционной матрицы кодов естественного языка нетрудно. На рис. 4 приведены соответствующие функции убывания модулей коэффициентов парной корреляции для русского, английского и татарского языков при использовании однобайтной кодировки.

Так как функции убывания модулей коэффициентов корреляции естественных языков известны, по ним легко можно восстановить значение модулей элементов связывающей матрицы a выражения (2). Переход от модулей коэффициентов корреляции к параметрам связывающей матрицы a осуществляется путем применения номограммы (рис. 1). Таким способом удается получать кодовые последовательности, полностью эквивалентные по их энтропии русскому, татарскому, английскому или любому другому естественному языку.

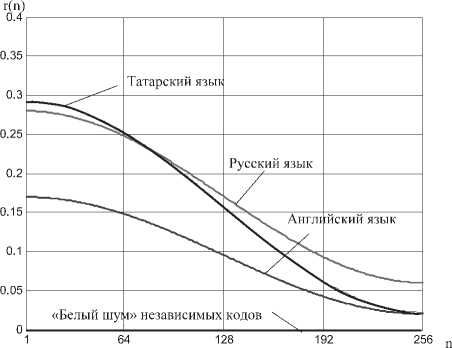
Рис. 4. Зависимость модулей коэффициентов корреляции естественных языков от расстояния до диагонали корреляционной матрицы

Примеры убывающих функций относительной энтропии (энтропии, приходящейся на один бит кода) для естественных языков и постоянная функция относительной энтропии белого шума приведены на рис. 5.

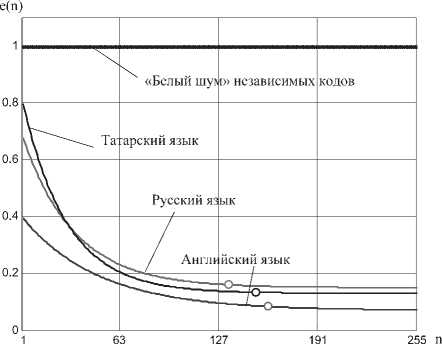
Рис. 5. Убывание относительной энтропии кодовых последовательностей русского, английского и татарского естественных языков

Из рис. 5 видно, что идеальный «белый шум» всегда обладает максимально возможной энтропией. Энтропия русского языка перестает изменяться для групп с числом букв более 17 (число бит n = 17-8 = 136). Как следствие, показатель экспоненты относительной энтропии русского языка составляет 17/3 = 6,4 буквы (45,3 бита).

Для английского языка стабильный участок начинается после 22 буквы (показатель затухания экспоненты составляет 7,1 буквы, или 56,8 бита). Для татарского языка изменение относительной энтропии прекращается для расстояний в 20 и более букв.

Исходя из приведенных данных, должны выбираться размерности генераторов имитационных кодов того или иного естественного языка. Так, для имитаторов кодов русского языка необходимо использовать в формуле (2) связывающие матрицы размерностью 136 параметров (17 знаков в 8-битной кодировке). При этом каждый такт работы 136-мерного генератора будет давать 136-битный кодовый пакет. Практика показала, что при генерации каждого из таких последовательных пакетов знаки элементов связывающей матрицы должны выбираться случайно. В итоге получается кодовая последовательность, хорошо воспроизводящая плотность распределения парных коэффициентов побитной корреляции кодов русского языка.

Для татарского языка приходится увеличивать размерность связывающей матрицы до 160 одновременно учитываемых параметров. Английский язык требует еще большего увеличения размерности связывающей матрицы – до 176 одновременно учитываемых параметров.

Заключение

Изложенный в данной статье подход к моделированию естественных и искусственных языков позволяет относительно малыми вычислительными ресурсами воспроизводить кодовые последовательности любой длины. При этом размерность связывающих матриц может составлять 136; 160; 176; 256; 512 и 1024 параметра. Технические ограничения, обусловленные применением классического подхода к моделированию [7], снимаются. Вычислительная сложность предложенных в данной статье процедур имитационного моделирования оказывается линейно связана с размерностью решаемой задачи. То есть удается снизить кубический рост сложности вычислений, характерный для классики [7], до линейной, что делает задачу легко реализуемой на практике.