Моделирование кольцеобразных структур углеродных нанотрубок как макромолекулярных клубков - возможность гелеобразования

DOI:

Как хорошо известно [17; 19], углеродные нанотрубки (нановолокна) формируют в полимерном нанокомпозите свернутые кольцеобразные структуры, внешне похожие на макромолекулярные клубки. Такое поведение указанных нанонаполнителей обусловлено их высокой степенью анизотропии и низкой поперечной жесткостью. В настоящее время предпринято несколько попыток использовать аналогию углеродная нанотрубка-макромоле-кулярный клубок для теоретических оценок [6; 17]. Очевидно, что указанная аналогия позволяет использовать хорошо разработанные методы как классической [1], так и фрактальной [13] физической химии полимерных растворов для анализа поведения углеродных нанотрубок в полимерных нанокомпозитах. В этом случае кольцеобразные структуры нанотрубок рассматриваются как макромолекулярный клубок, а полимерная матрица – как растворитель [17].

Такая трактовка нанокомпозитов поли-мер/углеродные нанотрубки делает необходимым исследование возможности реализации в них процесса гелеобразования, под которым понимается переход жидких (легкоподвижных и вязкотекучих) микрогетерогенных или гомогенных систем в твердофазное состояние геля или студня. Гелеобразование обусловлено возникновением в объеме жидкой системы пространственной фазовой или молекулярной сетки (каркаса), которая лишает систему текучести и придает ей некоторые свойства твердого тела (эластичность, пластичность, хрупкость, прочность), что представляет особый интерес при исследовании свойств полимерных нанокомпозитов [5].

Целью настоящей работы является исследование свойств нанокомпозитов полимер/ углеродные нанотрубки (нановолокна) в рамках теории перколяции и возможности реализации в них процесса гелеобразования.

Эксперимент

В качестве матричного полимера использован полипропилен (ПП) промышленного производства «Каплен» марки 01 030. Эта марка ПП имеет показатель текучести расплава 2,3–

3,6 г/10 мин, средневесовую молекулярную массу ~ (2-3) х 10⁵ и индекс полидисперсности 4,5.

В качестве нанонаполнителя использованы углеродные нанотрубки (УНТ) марки «Та-унит», имеющие наружный диаметр 20–70 нм, внутренний диаметр 5–10 нм и длину 2 мкм и более. В исследуемых нанокомпозитах ПП/ УНТ содержание таунита варьировалось в пределах 0,25–3,0 масс. %. Кроме того, использованы многослойные углеродные нановолокна (УНВ) с числом слоев 20–30 и диаметром 20–30 нм с длиной порядка 2 мкм. Содержание УНВ в нанокомпозитах ПП/УНВ варьировалось в пределах 0,15–3,0 масс. %.

Нанокомпозиты ПП/УНТ и ПП/УНВ получены смешиванием компонентов в расплаве на двухшнековом экструдере Thermo Haake модели Reomex RTW 25/42, производство ФРГ. Смешивание выполнено при температуре 463-503 К и скорости вращения шнека 50 об/мин в течение 5 мин. Образцы для испытаний получены методом литья под давлением на литьевой машине Test Sample Molding Apparate RR/TS MP фирмы Ray-Ran (Тайвань) при температуре 503 К и давлении 43 МПа.

Механические испытания на одноосное растяжение выполнены на образцах в форме двухсторонней лопатки с размерами согласно ГОСТ 112 62-80. Испытания проводились на универсальной испытательной машине Gotech Testing Machine CT-TCS 2000, производство ФРГ, при температуре 293 К и скорости деформации ~ 2 х 10^-3 с^-1.

Результаты и обсуждение

Авторы [6] предложили использовать для определения модуля упругости Е_н нанокомпозитов модифицированное правило смесей, которое в первоначальном варианте дает верхнее предельное значение модуля упругости композитов [7]:

Е н = Е м I ¹ — Ф н ^{) + ЬЕ}нан Ф н , ⁽¹⁾

где Ем и Енан – модули упругости матричного полимера и нанонаполнителя, соответственно, ф -объемное содержание нанонаполнителя, b<1 – коэффициент, отражающий степень реализации свойств нанонаполнителя в полимерном нанокомпозите. Параметр bЕнан по существу представляет собой эффективный модуль нанонаполнителя или, более точно, модуль кольцеобразных структур УНТ (УНВ) Еаэгфр .

Величину ф н можно определить согласно хорошо известной формуле [15]:

W

Ф н = / ,               (2)

ρн где Wн – массовое содержание нанонаполнителя, рн - его плотность, определяемая для наночастиц следующим образом [15]:

Р н = 188 ( D унт ) ^1/3 , кг/м³,           (3)

где D _УНТ – диаметр углеродных нанотрубок (нановолокон), который дается в нм.

Оценки согласно уравнению (1) показали, что величина снижается по мере роста содержания нанонаполнителя ф н от 51,6 до 9,9 ГПа для нанокомпозитов ПП/УНТ и от 34,9 до 5,5 ГПа для нанокомпозитов ПП/УНВ. Такое изменение Е _а ^э _г ^ф _р позволяет предложить следующее соотношение для описания этого изменения:

Е Тгр ~ Ф н Л              (4)

где Е _а ^Т _гр – теоретическое значение величины Е _а ^э _г ^ф _р , s – показатель, который был выбран равным 0,7 для нанокомпозитов ПП/УНТ и 0,6 – для нанокомпозитов ПП/УНВ.

На рисунке приведено сравнение величин Е _а ^э _г ^ф _р и Е _а ^Т _гр для рассматриваемых нанокомпозитов, которое показало их достаточно хорошее соответствие (среднее расхождение Е _а ^э _г ^ф _р и Е _а ^Т _гр составляет ~ 9,5 %). Рассмотрим физические основы применения соотношения (4) для описания модуля упругости кольцеобразных структур УНТ (УНВ). Как известно [14], для описания жесткости полимерных растворов около точки гелеобразования разработано несколько перколяционных концепций, которые дают следующее соотношение для описания их жесткости:

^Е ~ ⁽ Р — P c ) t , ⁽⁵⁾

где Е – модуль упругости полимерного раствора, р – степень конверсии, р_с – порог перколяции, t – перколяционный индекс.

Величина t варьируется в достаточно широких пределах в случае различных теоретических и экспериментальных работ (от 1,80 до 3,88 [14]), но общей тенденцией соотношения (5) является увеличение Е по мере роста р , которую в рамках предложенной аналогии следует рассматривать как объемное содержание нанонаполнителя ф _н . Это положение принципиально отличается от тенденции соотношения (4), которое показывает снижение Е Т_гр по мере роста ф _н . Последнее соотношение по своему физическому смыслу более соответствует соотношению, полученному в

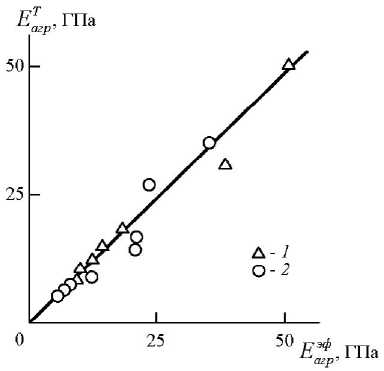
Сравнение эффективных модулей упругости кольцеобразных структур УНТ (УНВ) и , рассчитанных согласно уравнениям (1) и (4), соответственно, для нанокомпозитов ПП/УНТ ( 1 ) и ПП/УНВ ( 2 )

работе [3] для описания проводимости 2 случайной смеси двух компонентов:

2 ~ ( P - P c ) ’ ¹ . (6)

Указанное сходство позволяет предположить, что соотношение (4) характеризует не собственно жесткость кольцеобразных структур УНТ (УНВ), а их способность передавать приложенное механическое напряжение. Следовательно, в рассматриваемом случае величина является Е _а ^э _г ^ф _р аналогом проводимости. Сравнение соотношений (4) и (6) предполагает, что для углеродных нанотрубок (нановолокон) порог перколяции ф с =0. В рамках фрактального анализа точка гелеобразования или порог перколяции определяется следующим образом [8; 11]. Эффект гелеобразования, трактуемый как формирование стягивающего систему кластера, приводит к существенным изменениям параметров, описывающих эту систему, в точке гелеобразования [8]. Так, скорость перемещения кластеров (кольцеобразных структур) 3 с массой m предполагается равной [11]:

9 = т ^а . (7)

В точке гелеобразования показатель a изменяет знак с отрицательного на положительный. Это означает, что до точки гелеобразования большей подвижностью обладают меньшие кластеры, а за точкой гелеобразования наибольшей подвижностью будет обладать стягивающий кластер, поскольку его масса гораздо больше массы любой кольцеобразной структуры [8; 11].

Аналогичное резкое изменение показателя го в скейлинговом соотношении Смолуховс-кого в точке гелеобразования происходит в рамках концепции кинетического гелеобразования [8]. При го <0,5 для всего распределения размеров кластеров справедлив общий скейлинг и средний размер кластера регулярно растет со временем, а за точкой гелеобразования ( го >0,5) этот скейлинг нарушается: наиболее быстро растет наибольший кластер [8].

Зависимость радиуса кольцеобразных структур УНТ (УНВ) R _УНТ от продолжительности переработки t определяется следующим образом [12]:

1/ z

УНТ t ,

где показатель z связан с фрактальной размерностью кольцеобразных структур D f и показателем а уравнением [12]:

_z = D f ( 1 — _а ) _ ( d — 2 ) ,             (9)

где d – размерность евклидова пространства, в котором рассматривается фрактал (очевидно, в нашем случае d =3).

Величину R _УНТ можно рассчитать с помощью следующего перколяционного соотношения [9]:

„ = ^{n L} УНТ ^Г УНТ н    ( 2 R УНТ ) ³ ,

где L _УНТ и r _УНТ – длина и радиус углеродной нанотрубки (нановолокна), соответственно.

Как показали расчеты согласно уравнению (10), наблюдается снижение R _УНТ по мере роста j _н и при наибольших значениях ф _н , соответствующих W _h =3 масс. %, зависимости R _УНТ( ф _н ) имеют тенденцию выхода на асимптотическую ветвь [19], что предполагает достижение кольцеобразными структурами УНТ или УНВ своих минимальных значений R _УНТ. По аналогии с макромолекулярными клубками это означает достижение максимально плотной кольцеобразной структуры с максимальным предельным значением ее фрактальной размерности D_f ( D ^п _f ^р ), которая определяется согласно уравнению [10]:

D 7 = ^ d ^ ¹ ) .           (11)

Для d =3 величина D ^п _f ^р =2,286. Далее для оценки величины D_f можно использовать модель необратимой агрегации, которая описывает процессы полимеризации (формирования макромолекулярного клубка) и дает следующее соотношение для определения радиуса агрегата частиц R_агр [4]:

R arp ~ c - ¹ / ⁽ d - D f ) ,                  (12)

где с ₀ – исходная концентрация агрегирующихся частиц.

Коэффициент в соотношении (12) можно определить при следующих условиях: R arp = R УНТ , с 0 = Ф н и D f = D 7 . Значения R УНТ и Ф н приняты для W_H =3,0 масс. %. Как показали оценки согласно указанному соотношению, величина D f растет по мере увеличения ф н (снижения R _УНТ) от 1,91 до 2,29 для нанокомпозитов ПП/УНТ и от 1,76 до 2,21 для нанокомпозитов ПП/УНВ.

Показатели а и го связаны между собой следующим уравнением [8]:

d - 2

^ю = ^{а +}      .             (13)

Оценки согласно уравнениям (9) и (13) показали, что условие а =0 и го =0,5, необходимое для достижения точки гелеобразования УНТ (УНВ) реализуется только для D_f =1,0, то есть для полностью распрямленных нанотрубок (нановолокон) с R УНТ ^да . Получение нанокомпозитов полимер/углеродные нанотрубки при этих условиях может дать достаточно сильный эффект. Так, изготовление на-нокомпозитных волокон поливиниловый спирт/ многослойные УНТ с содержанием УНТ W_н =60 масс. %, полученных методом «коагуляционного вытягивания нити», который предполагает практически полную ориентацию УНТ в нанокомпозите ( D f ^ 1,0), позволило получить материал с прочностью 1800 МПа, тогда как прочность аналогичных нанокомпозитов, полученных традиционными методами, не превышает ~ 100 МПа [16].

И в заключение рассмотрим выбор показателя s в соотношении (4). Как показано в работе [3], аналогичный показатель в соотношении (6) можно оценить с помощью уравнения:

^ = d u - ( d - 2 ) ,              (14)

где v - критический перколяционный индекс, равный 0,88 [2], d_u – размерность неэкранированного периметра, оцениваемая согласно уравнению [3]:

(     \ d — Df du =(DJ-1)+—,         (15)

dw где dw – размерность случайного блуждания, принятая в дальнейшем равной 2 (броуновское движение).

Оценки согласно уравнениям (14) и (15) дали следующие значения показателя s : 0,410,57 для нанокомпозитов ПП/УНТ и 0,34-0,53 для нанокомпозитов ПП/УНВ. Как можно видеть, верхняя граница рассчитанных значений показателя s достаточно близка к величинам, выбранным в соотношении (4). Отметим, что экспериментальное доказательство возможности образования геля углеродными нанотрубками в их суспензиях дано в работе [18].

Выводы

Таким образом, результаты настоящей работы показали, что эффективный модуль упругости кольцеобразных структур УНТ (УНВ) характеризует не их жесткость, а способность передавать приложенное механическое напряжение. В отличие от полимеров, углеродные нанотрубки (нановолокна) обнаруживают эффект гелеобразования только в случае своей прямолинейной конфигурации. Достижение указанного эффекта может привести к резкому изменению свойств нанокомпозитов.