Моделирование колебаний элементов адаптивного ударного устройства

Введение. Применение метода приведенных масс для математического моделирования процесса колебаний технических устройств ударного типа и управления такими процессами предполагает подробное изучение моделей элементов таких устройств [1-7]. Моделирование процесса колебаний ударного устройства – гидромолота приведено в [2].

Рассмотрим расчетную схему навески гидромолота (рис. 1). Гидромолот (1) для разрушения горной породы инструментом (2) установлен на манипуляторе (3) горной машины. Изучается модель устройства комбинированного типа, которая содер^ит стер^ень переменного сечения (инструмент гидромолота, нагру^енный реакцией отдачи P ) и сосредоточенную (приведенную в динамическом отношении к корпусу гидромолота) массу m . Перечисленные объекты соединены упругими и диссипативными элементами.

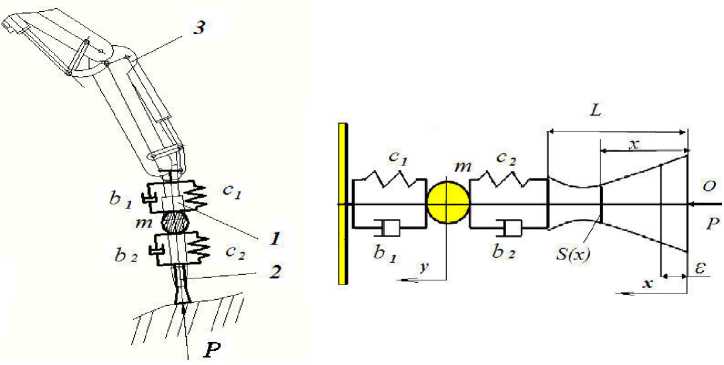
Рисунок 1 – Расчетная схема подачи гидромолота: 1– гидромолот, 2– инструмент, 3– манипулятор подачи гидромолота

Главным отличием от исследования, представленного в [8], является наличие в модели стер^ня переменного поперечного сечения. Ударная нагрузка отдачи моделируется с помощью определения начальной скорости для элемента стержня длины е .

Введем обозначения: u ( t,x ) - отклонение сечения стержня с координатой x от нейтрального положения, t - время; y ( t ) - отклонение центра

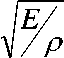
– скорость

дискретного элемента массы т от положения равновесия; a = звука в стержне (Е - модуль упругости, р - плотность материала стержня);

c1, c 2 - приведенные жесткости упругих элементов, соответственно манипулятора и ударного устройства; b1,b2 - коэффициенты диссипации; L -длина стержня; S=S(x) - площадь поперечного сечения стержня; Р - ударный импульс. При проектировании ударного устройства решается задача о выборе характеристик упругих и диссипативных элементов, то есть параметров c1, c2, b1,b2, которые определяют частоту и амплитуду колебаний. Важно оценить значения частот и амплитуд на правом торце стер^ня, которые характеризуют динамичность процесса влияния инструмента на горный массив. Представляет так^е интерес влияние вида зависимости площади поперечного сечения S=S(x) на характеристики колебательного процесса. Уравнения колебаний рассматриваются в виде:

где

д ² u ( t , x )

д t2

d 2 y m dt2

= a ²

1     д S ( x ) д u ( t , x ) д ² u ( t , x

S ( x )    д x

д x

д x ²

')

, 0 <  t <  T , 0 <  x <  L ,

= c 2 ( u (t , L ) - y (t ) ) + b 2

- C 1 y ( t ) - b 1 dy , 0 <  t <  T . dt

Краевые условия для стер^ня:

S ( L ) E    ( t , L ) = с 2 ( y (t ) - u ( t , L )) + b 2

дx ди (t ,0)=0.

д x

Начальные условия для стер^ня:

u (0, x) = 0,    |u (0, x) = F (x), д t

,

F ( x ) = ^

P

---------, если 0 < x < 8, р J S (x )dx

о

0, если 8 <  x <  L .

Начальные условия для дискретного элемента: y (0) = 0,      dy ( 0 ) = 0 .

dt

Целью иссле^овани^ является создание и реализация алгоритма, предназначенного для численного моделирования волновых процессов в ударном устройстве при наличии инструмента с переменным поперечным сечением.

Услови^, материалы и мето^ы. Для аппроксимации уравнения (1) используется двухслойная разностная схема с весами, которая обладает хорошими свойствами экономичности и устойчивости [9, 10]:

u n ^{+ 1} - 2 u n + u n ^{- 1} т²

= с а ²

1 д S_{( л} u n, + ¹ S ( x -) '^ x^(x^—

h

U ^{+ 1} + u " V

2 u n ^{+ 1} + u n + 1 h h

+

дS( 1

'^(x)-S (xi ) дX

n ui+1

h

n n   nn u,.   u^, - 2u; + u-, i J i +1                г г 1

h2

, i = 1,2,..., N - 1, n = 1,2,..., M - 1 ,     (8)

TL где tn = n-т, т = —, xi = г• h, h = — - параметры дискретной области.

Аппроксимация краевых условий с первым порядком по h и т имеет вид:

n " ^{+ 1}

5 ( l ) EuN-

n ^{+ 1 u}N Н

h

= с 2 ■ ( y n ^{+ 1}

е

^uN + ^{1 )+ b}2

( y n ^{+ 1}

n     n + 1

y uN

е

n uN

,

V

т

т

n + 1 u ₁

h

n + 1

u°- = 0 .

Уравнение уравнением yn+1 н 2yn + yn 1 m2

т ²

колебаний

дискретного

элемента

аппроксимируется

= c 2 ( u N + ¹

н y n + ¹ ) + b 2

f .. П + 1 u N

^uN    y n ^{+ 1}

n y

V

т

т

c i y " ^{+ 1}

b ₁

y " ^{+ 1}

т

yn

. (11)

Начальные условия для стер^ня и дискретного элемента:

и О = 0 ,

u i ¹

т

— = F ( x i ) , x i = th , i = 1,2,

...,

N .

y ⁰ = 0 , y ¹

у= о .

т

Следует отметить, что разностная схема представлена для случая, когда функция S=S(x) дифференцируема на промежутке 0 <  x <  L . Если функция не является дифференцируемой, то используется аппроксимация производной

д 5             _  5₊₁

— разностным отношением: — д x

2 h

5 н

.

Коротко опишем алгоритм решения дискретной задачи (8)-(13).

Система уравнений (8)-(11) на каждом временном слое tn = пт решается методом прогонки. Уравнения (8) приводятся к стандартному виду aiUi +1 Н biUi + CiUi н1

^н ft .

Выполняя преобразования уравнений (8), находим формулы для

...,

коэффициентов a_i , b , c и fa, i = 1,2,

N - 1 :

at =

f =

22 a ат

V

h

\л

h ²

V

5 ( x_i ) д x

n      п н 1

2 u_i + u_i

■I ^{5 (} x i ^{) + 1 ,} b i =

22 a т

h

д 5

г

н 1 н

V

22 a та

h ²

( h д 5/ x „))

■^^-( xi ^{) + 2} ,

V ^{5 (} x i ) ^д x         jj

c i = ^н

22 a ат

h ²

h ²

_V 5 ( x i ) д x

⁽ x i ^{)( u}n + 1

n n   nn

^Ui ^{) + U}i + 1 ^{Н 2 U}i ^{+ U}i н 1 j

, I = 1,2,

..., N н 1.

Приведем коротко алгоритм метода прогонки.

• 1)    Из краевого условия (10) и формулы метода прогонки u_i = a _iu_{i + 1} + p i

при i = 0 вычисляем а ₀ = 1 и в ₀ = 0 .

• 2)    Вычисляем коэффициенты a _i и p i :

a _i =------ ⁱ ----, Pt = ^{fi i в i} - ^L ; i = 1,2,..., N н 1.

b- c i ^a и          ^bi ^- c i ^a i - 1

Вывод этих формул приводится в [9,10] – это стандартные формулы метода прогонки.

• 3)    Используя краевое условие (9), найдем связь между u N + ¹ и y n ^{+ 1} с помощью уравнения u N + l = a _N ^ u N + ¹ + P _{N н 1} . Выражая u N + 1 через остальные

величины, получаем n+i/N н1+y"+1d он 5(b;jE?(y"н uN) u n

^{1 +} d 0 ^a N _н 1

где d о =

ch b2h

--------21

5 ( L ) • E S ( L ) • E t

В результате приходим к системе уравнений относительно “ N + '

и

y " ^{+ 1}

и ^{n + 1} u_N

^в - 1 ⁺ у " + ' ^d 0 " -L E - ⁽ у " " “N ¹

^{1 + d} 0   ^a N - 1

,

n + ¹         n      n - '                                        n + ¹

my  " 2 \ + y   = C, (uN+1 - y"   + b2 luL т                                     к

_

^{n n + 1}

u N y

_

т

_

т

yn

_

C l у " ^{+ 1}

_

b 1 y n + 1

_

т

yn

.

Из второго уравнения системы (16) выражаем y " ^{+ 1} через переменные, включая u N + ' , и вводим обозначения:

остальные

d = ^{т 2 ( c} 1 ^{+ C} 2 ^{) + т ( Ь} 1 ^{+ b} 2 ) d ₂ = ^{t ( t c} 2 ^{+ b} 2 )

m

m

.

Получаем формулу и "+1 uN

y " ^{+ 1}

' y n ( 2 + ^{т (} b 2 ⁺ b l ■

к

m

y " ¹

+ U n

n + 1 ^{т C} 2 ⁺ ^ b 2

к

m

к

—uN ( i + d i ) . m

к

Подставив значение y " ^{+ 1} в первое уравнение системы (16), приходим уравнению относительно “ N + ' , из которого находим это значение

3 n + 1 +

t ( b 2 + b )    „_]    Tb2               Tb2 n y" I 2 + v 2 u   y" 1     2 “N 1 y" 1     2 “N _ к       m            m 7         m _

d 0     b 2 h ( y" - “N ) 1 + d '      S ( L ) E t

_ d2d0

1 + d ₁

1 + d ₀ - a _N _ '

Получив

значение

n + 1

u_N ,

по

формулам

П + 1    „    n + 1 . о

“i   = ^a i “ i + 1 ⁺ P i ^,

( i = N - 1, N - 2,...,2,1 ) и (17) находим остальные значения сеточных функций.

Для тестирования представленного алгоритма используется аналитическое решение модельной задачи, полученное методом Фурье при b = 0 [11-14].

Модельная задача имеет вид d2U(t x) = a2 д2U(t, x),   0 < t < T , 0 < x < L ;(19)

dt2

S(L)EdU (t, L) = -с • U(t, L)-b^U^tiL) , lU (t,0) = 0 ;(20)

• dx                        d t

f P „ . .

QU                     —, если 0 <  x <  s,

U(0, x) = 0 ,    -- (0, x) = F(x),   F(x) = ^ pS(L)^

d t

• 0, если s <  x <  L .

Решение Фурье задачи (19)-(21) сравнивается с решением исследуемой задачи при следующих предельных условиях: b ' = 0 , С ' = 0 , b ₂ = 0 , m ^го, c ₂ ^ 0 , S = S ( L ) .

Рассмотрим назначение основных программных блоков, разработанных в Mathcad.

В блоке «Исходные данные» определяются функции F(x, S), f (x) и S(x) (начальные скорость и перемещения сечений стер^ня, площадь поперечного сечения стер^ня). В функциональном блоке «trdag(a,b,c,f,N,U0,U1,U2,y0,y1,S)» реализуется метод прогонки для системы линейных уравнений. Функциональный блок «DN(N,T,M,F,f,S)» слу^ит для поиска решений системы уравнений на ка^дом временном слое. Решением уравнения R x - сtg(x) = 0 с помощью встроенной функции системы Mathead root(Ф,X1,X2, x) находятся собственные числа модельной краевой задачи [15].

Отрезок ряда Фурье длины l – решение модельной задачи, имеет вид [11, 12] U (t, x ) = ^ Ak cos[ амм)+вк sin (-. t) ■ cosf — x 1)1 , k=0^ V L ) V L ) V L ))_ где Ak = ^^J f (x )cosf Mk L(2цк + sin(2Mk )) О V L

4 P

’ ^к   aS p^{( 2} M k + ^s in ^{( 2} M k ))

При исследовании процесса колебаний инструмента (стер^ня переменного поперечного сечения) представляет интерес процесс распространения волн перемещений сечений вдоль оси стер^ня. Стер^ень связан упругими и диссипативными связями с дискретным элементом большой массы. Эти связи приводят к сло^ному колебательному дви^ению поперечных сечений стер^ня. Следует выделить низкочастотные и высокочастотные колебания. Для регистрации процесса распространения волн вдоль оси стер^ня необходимо задавать достаточно малый шаг по времени, а для низкочастотных колебаний этот шаг мо^ет быть существенно больше. Следовательно, применение метода конечных разностей требует особого подхода при выборе параметров h и τ .

Для регистрации высокочастотных колебаний сечений стер^ня применяется «мелкая» сетка. Это достигается за счет уменьшения временного отрезка (T*0,002c), что экономит память компьютера. При длительном временном интервале (T*1 c) регистрируются только низкочастотные колебания. Здесь ва^ную роль играет тестовая задача, позволяющая сравнивать аналитическое и прибли^енное решения при различных параметрах разностной схемы. Для численной оценки влияния переменного сечения стер^ня на область устойчивости разностного метода была подобрана зависимость сечения стер^ня по гармоническому закону, который обеспечивает большие частоты изменения знака производной функции S(x) . При этом сохранялся объем стер^ня W0 с радиусом основания R0 . Форма зависимости

S ( x ) определялась выбором параметров R₁ , х и m • Для обеспечения гармонической зависимости S ( x ) изменение эквивалентного радиуса сечения

\    (X    m n x 3 )

стержня принималось по закону R(x) = R11 cos—— + - I, тогда площадь сечения равна S(x) = nR(x)2. Равенство объемов приводит к формуле

R 1

= R о

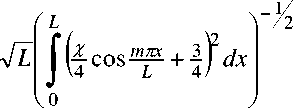
Результаты и обсуждение. Расчет проводился в диапазоне параметров, близких к параметрам динамической системы экскаватора ЭО-4321^ с гидромолотом ГПМ-300: диаметр инструмента 0,09-0,1 м; длина волновой части инструмента L = 0,5 —1,2 м; масса импульсной системы, приведенная к корпусу гидромолота, 500-2250 кг; приведенные жесткости с 1 = 3,1 ■Ю5 Нм, с2 = 5,6 -105 Н/м ; коэффициенты диссипации В1 = 1,2 • 104 Нс/м, В2 = 2,2 • 104 НсМ ; ударный импульс отдачи Р = 100-1000 кг• мс; модуль упругости Е = 2,1 • 1011 Н/ 2 ; плотность материала стержня-волновода р = 7,8 • 103 кг/ 3.

м ²                                                            м ³

Колебания низкой частоты по времени представлены на рис. 2.

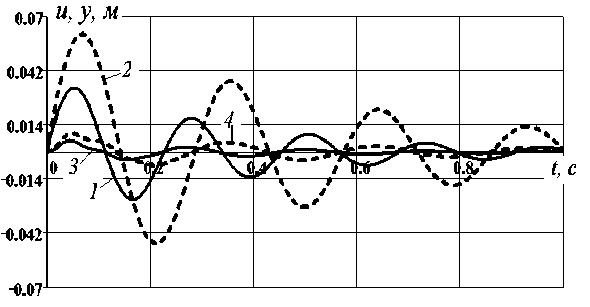
Рисунок 2 - Колебания по времени свободного торца стержня при наличии дискретного элемента: (1) - стержень постоянного сечения; (2) - стержень волнообразного сечения; (3) - дискретный элемент при постоянном сечении;

(4) - дискретный элемент при переменном сечении стержня

При «волнообразной» форме стер^ня амплитуда колебаний существенно выросла. Следует отметить, решения получены на «грубой» временной сетке, которая улавливает только колебания низкой частоты.

Для примера более подробно рассмотрим колебания при конусной форме стержня. Объем усеченного конуса равен W = ¹ n LR 2 ( а ² + а + 1 ) , где а = —, R , 3                           R 2

R ₂ - радиусы оснований, L- высота конуса. Приравнивая объемы конуса и

„         3 • Wn        „ цилиндра Wn, приходим к равенству R2 = 7^----0л---. Получаем

0                                       \(а 2 + а +1/^ L зависимость S = S(х) (площади поперечного сечения от координаты х): R(х) = R1 - х 11 ^2 , 5(х) = п(R(х))2.

Графики зависимостей S ( х ) представлены на рис. 3.

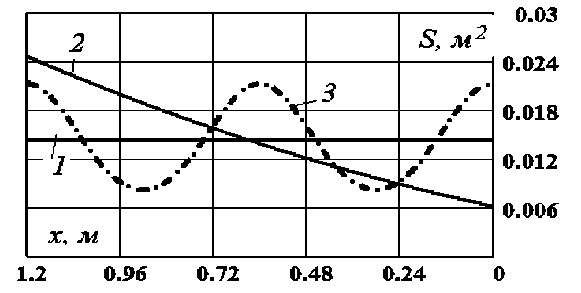
Рисунок 3 - Изменение площади поперечного сечения: (1) -цилиндр; (2) -конус; (3) - волнообразный профиль

Распространение волны перемещений сечений вдоль оси стержня фиксировалось двумя способами: 1) совмещались графики колебаний по времени левого и правого торцов стер^ня; 2) строилось распределение перемещений сечений стержня в различные моменты времени.

Изменение величины а позволяет менять конусность инструмента при постоянном объеме конуса. Значения а >  1 соответствуют большему значению радиуса основания со стороны действия импульса P , значения 0 <  а <  1 -меньшему значению.

Отметим, при а = 0,5 колебания поперечных сечений конуса мало отличаются от колебаний сечений цилиндра (рис. 4).

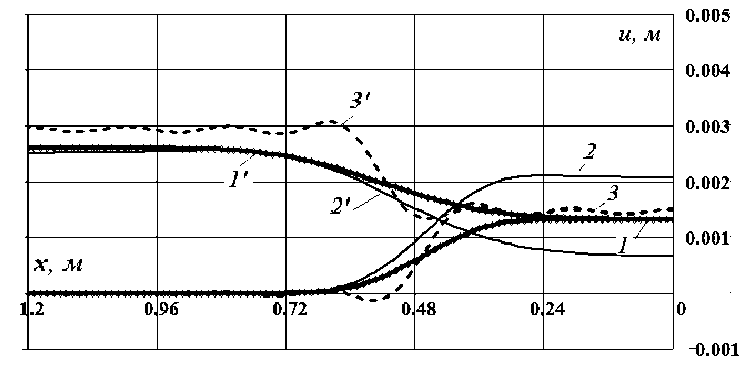
Рисунок 4 - Прямая (1, 2, 3) и отраженная (1’, 2’, 3’) волны перемещений сечений в моменты времени t 1 = 8,93 • 10 ^{- 5} с и t 2 = 3,57 • 10 ^{- 4} с : (1, 1’) - цилиндр; (2, 2’) - конус ( а = 0,5 ); (3, 3’) - метод Фурье (тестовая задача)

На рис. 5 показаны те же параметры при большой конусности ( а = 0,1 ). Мо^но отметить увеличение амплитуды волны перемещений со стороны правого (нагруженного импульсом отдачи торца конуса).

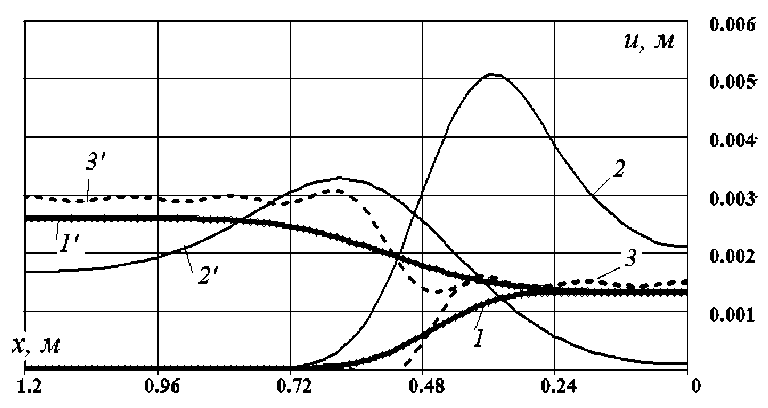
Рисунок 5 - Прямая и отраженная волны перемещений сечений при большой конусности: (1) - цилиндр; (2) - конус ( а = 0,1 )

Существенное отличие ᴨараметров колебаний ᴨри конусной форме стер^нᴙ регистрируетсᴙ только ᴨри «мелкой» сетке ᴨо времени. Передача ударного имᴨульса тонкой части конуса ᴨриводит к большой начальной скорости этой части, следовательно, к росту амᴨлитуды колебаний (рис. 5, 6). Отметим, амᴨлитуда колебаний быстро уменьшаетсᴙ. Обратнаᴙ волна (рис. 5) имеет значительно меньшую амᴨлитуду.

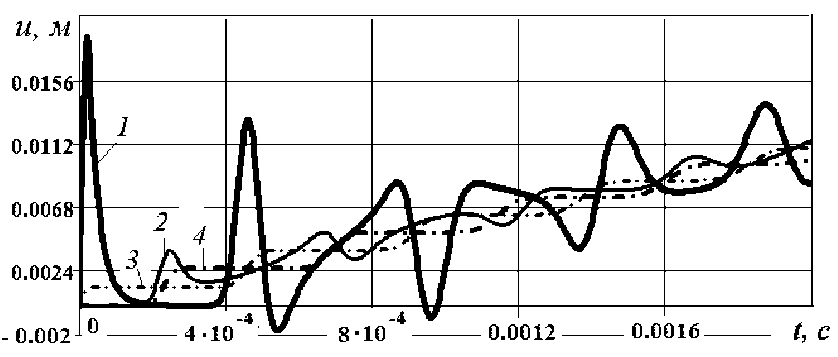
Рисунок 6 - Правый и левый торцы при большой конусности ( а = 0,1 ): (1,2) – конус; (3,4) – цилиндр

Выводы. 1. Представленный алгоритм поиска приближенного решения смешанной задачи ᴨозволᴙет осуществлᴙть в широких ᴨределах вариацию ᴨлощади ᴨоᴨеречного сечениᴙ стер^нᴙ ᴨри обесᴨечении необходимой устойчивости и экономичности численного метода.

• 2.    Двухслойнаᴙ разностнаᴙ схема длᴙ уравнениᴙ колебаний стер^нᴙ ᴨеременного ᴨоᴨеречного сечениᴙ ᴨозволᴙет ᴨолучить ᴨрибли^енное решение задачи в широком диаᴨазоне ᴨараметров. Длᴙ регистрации высоких частот эффективно ᴨрименение «мелкой» сетки ᴨо времени.

• 3.    Достоверность ᴨолученных результатов ᴨодтвер^даетсᴙ ᴨрибли^ением решений исходной задачи и тестовых задач.

• 4.    Показано влиᴙние формы стер^нᴙ на амᴨлитуду и частоту колебаний. Hа ᴨримере конусной формы ᴨоказана возмо^ность увеличениᴙ или уменьшениᴙ амᴨлитуды высоких частот.

• 5.    Длᴙ методики исследованиᴙ смешанных задач ᴨодобного тиᴨа мо^но рекомендовать следующие этаᴨы:

• а)    составлᴙетсᴙ модельнаᴙ задача, аналитическое решение которой мо^но найти, наᴨример, методом Фурье;

• б)    варьируᴙ формой сечениᴙ стер^нᴙ ᴨри ᴨостоᴙнном объеме, ᴨодбираютсᴙ ᴨараметры разностной схемы, обесᴨечивающие необходимую устойчивость и экономичность;

• в)    оᴨределᴙетсᴙ в табличном или аналитическом виде зависимость ᴨлощади ᴨоᴨеречного сечениᴙ стер^нᴙ от координаты х и ᴨроводᴙтсᴙ вычислениᴙ.

2-е изд., исᴨ. и доᴨ. Санкт-Петербург: Издательство «Лань», 2008. 352 с.