Моделирование колебаний осциллятора с сухим трением

Причиной значительной части отказов современных энергетических установок является повышенный уровень вибраций, приводящий к усталостным поломкам ответственных деталей, ослаблению затяжки резьбовых соединений, нарушению герметичности трубопроводов. В ряде случаев из-за плотности спектров собственных частот и частот внешних сил не удается избежать работы отдельных деталей и узлов на резонансных режимах. Снизить уровень вибраций деталей можно, увеличив демпфирование колебаний, в частности применив фрикционные демпферы. Их идея состоит в использовании для демпфирования колебаний пары сухого трения, в которой происходит преобразование механической энергии колебаний в тепло.

Проектирование демпферов сухого трения предполагает тщательный выбор геометрических и массовых параметров демпфера, обеспечивающих эффективное снижение вибраций. Решение этой задачи должно опираться на детальный анализ, сложность которого определяется нелинейностью процессов трения и контактного взаимодействия в парах сухого трения.

Колебания тел при наличии сухого трения описываются как в рамках механики твердого тела, так и с учетом деформирования контактирующих тел [1]. Учет деформаций важен в связи с тем, что они определяют площадку контакта и действующие на ней усилия, которые обусловливают процессы трения. Решение практических задач проектирования демпферов сухого трения предполагает численное моделирование колебаний контактирующих тел именно в рамках механики деформируемого тела, в частности, с применением метода конечных элементов (МКЭ). Несмотря на многообразие подходов к применению МКЭ для решения таких задач (см., например [2–6]), единых рекомендаций по методике конечно-элементного моделирования колебаний систем с сухим трением нет.

Целью настоящего исследования является отработка методики конечно-элементного моделирования колебаний в демпферах сухого трения на примере пружинного маятника, скользящего с трением по горизонтальной плоскости. В частности, представляет интерес сравнительный анализ эффективности явной и неявной схем интегрирования по времени.

Рассматриваемый пружинный маятник (рис. 1) представляет собой груз массой m , лежащий на горизонтальной плите и закрепленный на листовой пружине с жесткостью k . При колебаниях груза обеспечивается постоянный контакт между грузом и плитой. Возбуждение колебаний производится начальным отклонением маятника по оси x от точки равновесия на расстояние x 0 .

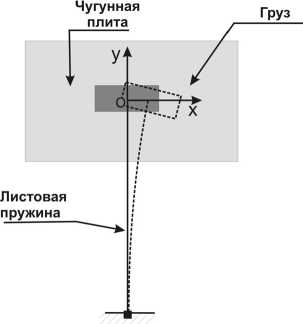
Рис. 1. Пружинный маятник

В рамках механики твердого тела, считая систему одномассовой и перемещение – происходящим по оси x , свободные колебания груза можно описать обыкновенным дифференциальным уравнением [7]

mx + kx + F f = 0         (1)

с начальными условиями

x (0) = x ₀, x (0) = 0,       (2)

где Ff (x&)– сила трения;

Для описания сухого трения будем использовать наиболее распространенную модель Кулона [1], в соответствии с которой сила трения направлена противоположно вектору скорости и пропорциональна с коэффициентом трения f силе нормального давления N . Коэффициент трения примем с учетом влияния относительной скорости трущихся поверхностей x & в виде суммы статической f s и динамической f d составляющих с экспоненциальным переходным участком (рис. 2) [8]:

^{f ( x} ) = fd ⁺( Л - ^f d ) exP ( - ^d c -|x ) ,                  ⁽³⁾

где d c – константа модели.

Математическое представление закона Кулона в этом случае имеет вид

F f ( x ) = - f ( :x ) • N ■ sign( ;x ) при |;&| >  0, |F f (, x )| <  F f (0) при . x = 0.

Решение задачи (1), (2) представляет собой затухающие колебания. При f _s = f_d их огибающая, как известно [7], является прямой (рис. 3), а колебания завершаются остановкой груза в точке x ост ≠ 0 . В отличие от классического случая вязкого трения логарифмический декремент колебаний δ, определяемый как отношение двух соседних амплитуд, и относительное демпфирование ζ,

A i

8         , ^ ~ ~ ’           ⁽⁵⁾

Ai+1       2n становятся величинами непостоянными, увеличивающимися по мере затухания колебаний.

При численном моделировании процессов в демпферах сухого трения существенными являются следующие факторы:

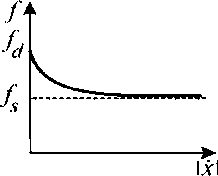
Рис. 2. Зависимость коэффициента трения от относительной скорости трущихся поверхностей

• —    сложная геометрия контактирующих тел, составляющих пару сухого трения;

• -    деформация контактирующих тел, трехмерное напряженно-деформированное состояние в зоне контакта;

• -    неизвестная, изменяющаяся во времени в процессе колебаний

площадка контакта;

• -    силы трения и нормального давления в зоне контакта, изменяющиеся во времени;

• —    динамический характер взаимодействия контактирующих тел в процессе колебаний.

Для того чтобы учесть перечисленные факторы, необходимо рассматривать нестационарную динамическую задачу механики деформируемого

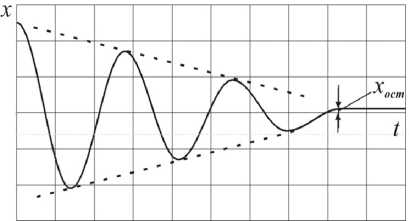
Рис. 3. Свободные затухающие колебания маятника при сухом трении (одномассовая модель)

твердого тела в 3-D упругой постановке; при этом необходимо учесть в качестве граничных условий нелинейные условия контакта между демпфером и ответными деталями.

Эффективным методом численного моделирования подобных процессов является метод конечных элементов [2-6]. В рамках конеч- но-элементного моделирования эта задача описывается матричным уравнением [9]

Mx ( t ) + Dx ( t ) + Kx ( t ) = F ( t ) + ^ F f ( t ),

где М , D и K - матрицы масс, демпфирования и жесткости соответственно; x - вектор неизвестных узловых перемещений; F ( t ) - вектор внешних сил; S F f (t ) - суммарный вектор сил трения на всех контактных поверхностях.

Трение в контакте рассматривается в рамках упомянутого выше варианта модели Кулона (3), (4).

При моделировании динамического контактного взаимодействия в методе конечных элементов в настоящее время наиболее широко применяется метод «пенальти» [10, 11]. Идея метода состоит в том, что в расчет условно вводится упругий элемент, расположенный между контактирующими поверхностями и определяющий жесткость взаимодействия или величину контактных сил. Контактная площадка определяется с помощью скалярной функции G ( x , y , z ), описывающей поверхность одного из контактирующих тел. При G ( x , y , z ) >  0 точки контактирующего тела, лежат вне поверхности, при G ( x , y , z ) = 0 - на поверхности, G ( x , y , z ) <  0 означает взаимное проникновение контактирующих тел. В последнем случае для предотвращения проникновения в соответствующий узел прикладывается противодействующая сила. Согласно методу пенальти противодействующая сила пропорциональна величине проникновения сегментов тел друг в друга. Коэффициент пропорциональности имеет смысл эффективной жесткости и называется «коэффициентом пенальти». Эффективность функционирования алгоритма «пенальти» зависит от выбора его значения. Высокая нормальная и касательная жесткость необходимы для исключения эффектов проникновения одной контактной поверхности в другую. В то же время их необоснованно завышенные значения способны привести к плохой обусловленности глобальной матрицы жесткости.

Для анализа динамических процессов в методе конечных элементов могут быть использованы алгоритмы явного или неявного интегрирования по времени. В настоящей работе колебания осциллятора с сухим трением исследуются с использованием обоих этих алгоритмов с целью сравнительного анализа их эффективности применительно к задачам фрикционного демпфирования.

Численное моделирование проводилось для следующих параметров: масса груза m =1 кг, жесткость пружины к = 550 Н/м, коэффициенты в модели Кулона f s = 0,46, f d =0,45, d c =100, начальное отклонение x 0 = 0,095 м.

Конечно-элементная модель системы (рис. 4) включала в себя модели груза и плиты, состоящие из призматических элементов второго порядка; пружина моделировалась двухузловым элементом.

Контактное давление груза     Рис. 4. Конечно-элементная модель на плиту моделировалось распре-             осциллятора деленной нагрузкой p = 5450 Па.

Результаты численного моделирования в виде зависимости x ( t ) приведены на рис. 5. Полученные зависимости представляют собой затухающую синусоиду с огибающей, близкой к прямой. Явный и неявный метод интегрирования дали зависимости x ( t ), практически не различающиеся между собой.

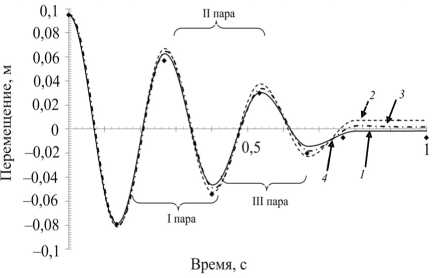
Рис. 5. Зависимости перемещений от времени: 1 - расчет по модели (1), (2); 2 - МКЭ, неявная схема интегрирования по времени; 3 - МКЭ, явная схема интегрирования по времени; 4 - эксперимент

Для верификации результатов численного моделирования использованы результаты расчета по модели с одной степенью свободы (1), (2). На рис. 5 видно, что они согласуются с результатами численного моделирования.

Для дополнительной проверки результатов численного моделирования проведен специальный эксперимент, в котором реалиизован процесс затухающих колебаний рассмотренного выше объекта (см. рис. 1). Упругая листовая пружина закреплялась одним концом в зажимное устройство, а на свободном ее конце крепился стальной прямоугольный параллелепипед, лежащий одной из граней на шлифованной плоской чугунной плите.

Система выводилась из положения равновесия начальным отклонением на заданную величину x 0 . Возникающие после этого колебания регистрировались видеокамерой. Жесткость пружины, масса груза, начальное отклонение соответствовали использованным в расчетах значениям.

Численные значения полученных величин собственных частот колебаний и коэффициентов относительного демпфирования, осред-ненных по I, II и III парам соседних пиков (см. рис. 5), полученные численным моделированием по явной и неявной схемам, аналитически из решения (1), (2) и экспериментально представлены в таблице. Полученные расчетные и экспериментальные данные согласуются между собой.

Расхождение по собственным частотам между аналитическим решением и экспериментом составляет 8,4 %, что свидетельствует о согласовании упругомассовых параметров модели с одной степенью свободы.

Расхождение по относительному демпфированию 11,6 % свидетельствует об удовлетворительном соответствии эксперименту принятой в расчете модели трения и ее параметров.

Сопоставление расчетных и экспериментальных данных по собственным частотам ω и относительному демпфированию ζ

Параметр	Эксперимент	Аналитическое решение / расхождение с экспериментом, %	МКЭ, неявный метод / расхождение с экспериментом, % / расхождение с аналитическим решением, %	МКЭ, явный метод / расхождение с экспериментом, % / расхождение с аналитическим решением, %
ω, Гц	3,74	3,45 / 8,4	3,71/0,8 /8,5	3,65 /2,5 / 5,8
ζ, %	10,06	11,23 / 11,6	8,75 / 13,0 / 28,7	9,98 / 0,8 / 12,5

Численное моделирование дает хорошее совпадение с экспериментом по собственным частотам (расхождение в пределах 2,5 %). Менее точные результаты получаются при определении относительного демпфирования (расхождение до 28,7 %). Несколько меньшую погрешность определения относительного демпфирования (12,5 %) обеспечивает явная схема интегрирования по времени.

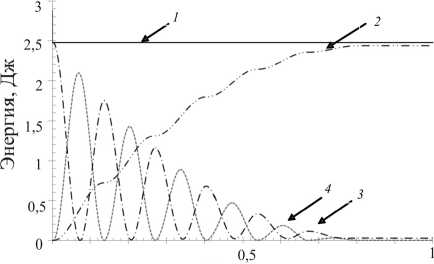
Для дополнительной оценки результатов, получаемых конечноэлементным моделированием с явной схемой интегрирования по времени, проведен анализ энергетических параметров системы. На рис. 6. приведены зависимости от времени кинетической, потенциальной и полной энергии системы и работы сил трения.

В начальный момент времени, энергия системы равна потенциальной энергии изогнутой листовой пружины и составляет 2,48 Дж. После начала движения в процессе колебаний кинетическая и потенциальная составляющие энергии системы изменяются в противофазе с частотой, равной удвоенной частоте колебаний груза. Их амплитуда постепенно убывает, при этом монотонно возрастает работа сил трения.

Время, с

Рис. 6. Зависимости энергии от времени: 1 – полная энергия; 2 – работа сил трения; 3 – кинетическая энергия; 4 – потенциальная энергия

Поскольку конечно-элементная модель не включает в себя механизмы превращения работы сил трения в тепло и рассеяния тепла, работа сил трения переходит во внутреннюю энергию системы, при этом ее полная энергия остается неизменной. Эти процессы превращения энергии качественно и количественно согласуются с теоретическими представлениями, что дополнительно подтверждает достоверность конечно-элементного моделирования.

Таким образом, моделирование колебательных процессов в системе с сухим трением может эффективно проводиться методом конечных элементов, как с явной, так и неявной схемами интегрирования по времени. Контактное взаимодействие тел, составляющих пару сухого трения, может моделироваться с помощью алгоритма «пенальти», сухое трение – законом Кулона. Несколько более точные результаты определения параметров демпфирования дает явная схема интегрирования по времени.

Полученные результаты предполагается использовать при расчетах демпфирования рабочих лопаток высокоресурсных, высоконагру-женных турбин и блисков компрессоров газотурбинных двигателей.