Моделирование колебаний звена технологической машины в режиме динамического торможения асинхронного двигателя при частотном управлении

Введение. В режиме разгона, торможения частотного асинхронного электропривода (ЭП) исполнительного механизма (ИМ) технологической машины (ТМ) в подвижных звеньях могут возникать вынужденные колебательные процессы, отрицательно влияющие на точностные показатели технологического оборудования (ТО), долговечность и эксплуатационные возможности средств автоматизации [1, 2]. Проанализированы причины возникновения колебательных процессов и определены их виды в ТМ [3, 4]. В зависимости от характера изучаемого явления и цели исследования колебаний в ТМ число степеней свободы движения звена ИМ определяют по расчетной схеме, приближенно отражающей конструктивные особенности исследуемого узла [4, 5]. Поставлена задача гашения колебаний звена подвижности ИМ с одной степенью свободы, в частности, захватного устройства (ЗУ) промышленного робота (ПР) с частотно-управляемым электроприводом (ЧУЭП) на базе короткозамкнутого АД.

Постановка задачи . При проектировании новых высокопроизводительных ТМ на базе ЧУЭП, функционирующего по схеме автономный инвертор напряжения (АИН) – асинхронный двигатель (АД), появляется необходимость в предварительной оценке параметров колебательности упругой системы: безударные движения ИМ в начальный период разгона и более сложные процессы торможения, обеспечивающие остановку ИМ в заданном положении с учетом прогнозируемой точности. Колебательность движения ИМ (звена подвижности ТМ) зависит от ряда факторов: массы звена подвижности, скорости перемещения и интенсивности торможения системы [1, 3]. Для оценки параметров колебаний отдельных звеньев ТМ обычно используют специальную измерительную аппаратуру, которую можно заменить виртуальными моделями инструментального оснащения и расширенных возможностей, выполненных в программном пакете Matlab+Simulink [6].

Математическая модель. Для поиска метода гашения колебаний выходного звена подвижности – захватного устройства (ЗУ) с консольным креплением в направляющей цилиндрической системы координат ПР «Электроника НЦТМ-01» была составлена упрощенная расчетная схема (рис.1).

Рис.1. Упрощенная расчетная схема взаимодействующих усилий в направляющих звена подвижности ПР

При анализе расчетной схемы принято равномерное распределение массы руки ПР, а массы ЗУ и транспортируемого груза сосредоточены в одной точке. Рассмотрены основные силовые соотношения в схеме (рис.1) с определением реакций в опорах при нулевых значениях А и В изгибающих моментов относительно точек А и В с учетом параметров [1]: а – вылет консоли направляющей (ход объекта манипулирования), ℓ – расстояние между опорами; d – диаметр направляющей; f – коэффициент трения между направляющей и втулкой конструкции. ξ – ускоре- ние свободного падения, q – распределенная нагрузка звена подвижности; G – вес груза; Q1, Q2 – силы трения в опорах А и В соответственно, F – движущая сила.

Значения реакций опор А и В определяются соотношениями [3]

Р _ 2G(a - fd) - q(f² - a^ ) - 2qfd(l + a)

RA =

Rb = G(l + a - fd) + q(l + aM^+a - fd) .(2)

Для поиска деформации руки робота по оси X в точке D (рис.1,б) использовался интеграл Мора [4], что позволило определить перемещение ЗУ под действием приложенных нагрузок x = - Gk1 - qk2, где k1 и k2 – коэффициенты при сосредоточенной и распределенной нагрузках, определяемые выражениями:

ci "3      / ki = — [2( - +1) - f- (- + 3(1 - f))],(4)

6 Ej   aa a a '1         d l'2               I              I                      Il k2 = —- [2 f- (— - (3 + 2 -) + 6 fd (- +1)) + (3 + 4----)],(5)

24Ej    a a         a       a            aa где E – модуль упругости при прогибе.

Если под сосредоточенной силой G (рис.1) принять алгебраическую сумму силы тяжести и силы инерции, тогда:

G = -mx - mg,(6)

где m – масса перемещаемого груза.

Для перехода к анализу динамики перемещения центра масс ЗУ ось следует направить в сторону действия силы тяжести (по оси Х) и, после некоторых преобразований, можно записать неоднородное дифференциальное уравнение x + k^X = G ,(7)

где ki =   1- и G = g + qk21 ,(8)

у mkii где k11, k21 – коэффициенты различия направленности силы трения при четных и нечетных колебаниях ЗУ.

В результате математического моделирования [7] были получены графические зависимости колебаний ЗУ в точке позиционирования (рис.2) для различных перемещаемых масс (груза) без изменения условий торможения.

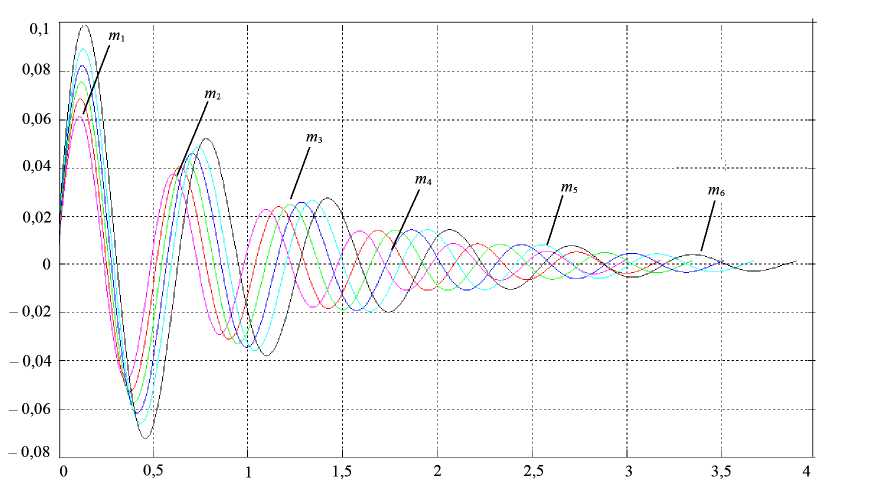
Рис.2. Зависимость колебаний ЗУ манипулятора в точке позиционирования при нагрузке от 1 до 12 кг ( m 1 =1, m 2 =3, m 3 =5, m 4 =7, m 5 =9, m 6 =12 кг)

Для измерения амплитуд и фаз вынужденных колебаний при моделировании колебательных процессов использовался виртуальный инструментарий – фазочастотометр (рис.3), позволяющий методом сравнения [6] определять искомые параметры гармонических колебаний.

Вход

Смещение входа

Выход

Смещение выхода

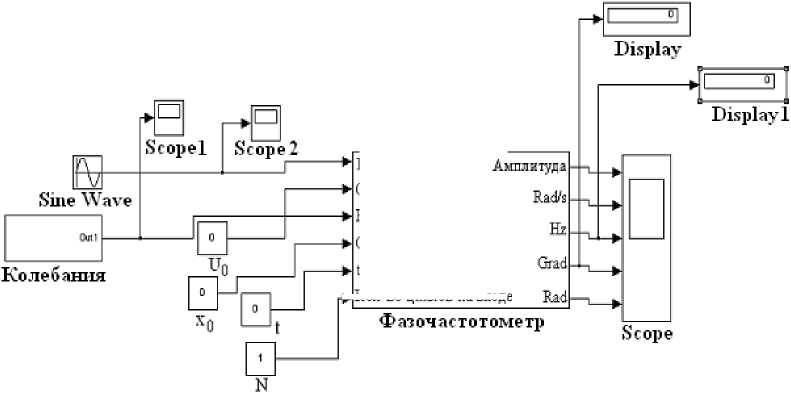
Рис. 3. Схема подключения фазочастотометра

t начала измерения

* Кол -во циклов на входе

Процесс измерения включает этапы:

• –    считывание с входа интервала времени, по истечении которого устанавливаются стационарные колебания;

• –    измерение длительности одного полупериода колебания входного сигнала и смещения выходных колебаний по отношению к входным колебаниям;

• –    вычисление фазы (Ф = 2 π ( l /2 D ) с учетом постоянных смещений входных U 0 и выходных X 0 колебаний, поскольку последние могут происходить относительно ненулевого уровня.

Результаты выполненных измерений параметров колебательного процесса позволяют построить взаимные зависимости (рис.4).

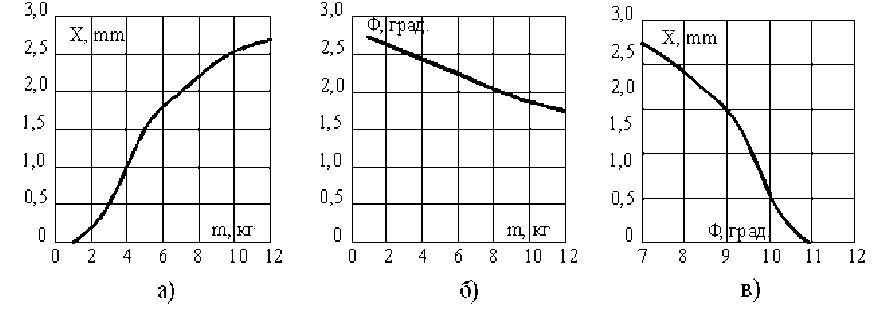
Рис.4. Взаимные зависимости колебаний: а – амплитуды от массы; б – фазы колебаний от массы; в – амплитуды колебаний от фазы

Полученные зависимости расчетной схемы могут быть использованы в качестве входных переменных для реализации алгоритмов нечеткой логики при управлении частотным электроприводом ИМ ТМ, а также исходными величинами для решения сложной задачи по снижению колебаний ЗУ в процессе работы ПР. Применение ЧУЭП характеризуется возможностью программного управления гашением колебаний ЗУ в процессе регулирования постоянного тока фазы АД в режиме двухтокового динамического торможения [1, 2]. При этом формируются расчетные динамические моменты на валу АД и исключаются возможные удары в механической части ЭМС [1, 3]. Такая система управления АД позволяет (по сигналам датчиков контролируемых величин) в соот- ветствии с приведенными зависимостями (рис.4) формировать целесообразное торможение звена подвижности в режиме демпфирования колебаний амплитуды ЗУ на определенном уровне (от 0,2 до 0,7 мм), зависимом от чувствительности датчиков и коэффициента усиления сигналов в СУ. В общем случае, процесс торможения АД можно рассматривать как результат взаимодействия эквивалентного двигательного и тормозного моментов на валу, обеспечиваемых равенством намагничивающих сил постоянного тока подмагничивания статора [1, 7] и приведенного значения переменного тока ротора АД. Использование двухтокового способа формирования тормозного момента для гашения колебаний ЗУ при подаче импульсов тока (рис.5) возможно в режиме импульсного регулирования тока подмагничивания, когда интегральная площадь импульса постоянного тока приравнивается к интегральной площади соответствующего периода колебаний звена подвижности, ЗУ. Начало периода формирования импульсов тока подмагничивания статора должно совпадать по времени с периодом вынужденных колебаний звена подвижности, ЗУ, но действовать в противофазе.

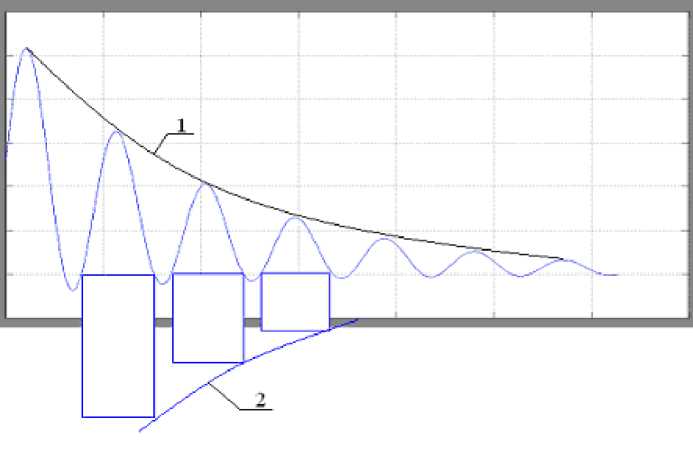
Рис.5. Метод гашения колебаний ЗУ ПР в процессе позиционирования

Такое управление электроприводом возможно при программном управлении и наличии силомоментных датчиков на конструктивных элементах ИМ, датчиков контролируемых параметров информационного канала СУ. При этом решение задачи управления ЭП предполагает разработку соответствующего программного обеспечении (ПО) и предсказуемость изменений контролируемых колебаний ЗУ (кривая 1 , рис.5), а также возможность формирования импульсов тока подмагничивания обмотки статора АД с оценкой интегрального значения площади каждого импульса, ограниченными экспоненциальной кривой 2 затухания колебательного процесса. Для реализации решения необходимо выбрать датчики измеряемых величин по фазочастотным характеристикам и диапазонам контролируемых параметров. При усложнении задачи исследования и необходимости расширения функциональных возможностей датчиков целесообразно применять известные решения виртуальных приборов. Такая необходимость появляется при управлении, например, ЧУЭП ТМ как сложным объектом в условиях неопределенности с использованием алгоритмов нечеткой логики.

Выводы. Моделирование вынужденных колебаний звена подвижности ТМ, обусловленных процессами «разгона-торможения» электропривода, позволяет:

• –    определить характерные зависимости вынужденных колебаний от внезапного изменения скорости движения, тормозного усилия и инерционных составляющих перемещаемых масс ИМ;

• –    разработать направления по совершенствованию конструкции звена подвижности и направляющих ТМ, выбрать рациональное сочетание механических характеристик электропривода и ИМ (ЗУ).