Моделирование колебательной системы сошник - почва

Машинное выполнение технологических операций характеризуется показателями, определяющими условия нормального функционирования систем и подсистем, выполняющих в машине основные и вспомогательные процессы. Эти показатели обоснованы закономерностями, взаимосвязями и взаимозависимостями между совокупностью физических взаимодействий (механических, гидравлических, биологических, электромагнитных и др.) и реакциями на эти взаимодействия со стороны исполнительных подсистем [1].

В сельскохозяйственных машинах выполняемый технологический процесс, как правило, устанавливают вначале подбором режимов и параметров исполнительных систем и последующей соответствующей их настройкой в полевых условиях. При проходе агрегатов в поле со стороны неровностей поля возникают дополнительные воздействия, чаще всего реализуемые в виде колебаний и вибраций в механизмах (подсистемах) машин и агрегатов, нарушающие установочные режимы и параметры.

Однако главной отличительной особенностью вибрации как физического эффекта одного из видов механических воздействий является возможность передачи энергии системе большой удельной мощности при малой амплитуде ее смещения за период колебаний. Вместе с тем, возможность регулирования параметров вибрации (частот и амплитуд) в широких пределах позволяет распространить ее действие на широкий спектр физических процессов. Универсальность вибрации состоит в том, что это наиболее эффективное общее средство управления динамическим состоянием систем при осуществлении различных технологических операций. Роль вибрации не только в том, что она приводит к интенсивному движению частиц или звеньев друг относительно друга в объеме системы, но и в том, что при этом резко увеличиваются скорости движения каждой частицы или звена в отдельности относительно центра масс.

Широкие возможности управления процессами в частотной области делают эту отрасль все привлекательнее в смежных отраслях науки, в частности, в сельхозмашиностроении. В отличие от общепринятого мнения о вредности вибрации, появляется возможность управления динамическими состояниями систем, выполняющих технологические процессы, используя их внутренние характеристики, что освобождает их от необходимости применения дополнительных контролирующих или управляющих систем, искусственно привносимых в конструкцию машины.

В основе выбора высокоточных технологий культур в условиях рискованного земледелия лежит необходимость передачи энергии частицам семян и почвы возможно большей удельной мощности при малых воздействиях на них, что возможно при использовании процессов вибрации. Эффект вибрации состоит в том, что возможно резкое увеличение скорости движения частиц относительно центра масс в объеме систем. Внесение в систему направленного вектора этих скоростей позволяет упорядочить процессы движения частиц (семян, почвенных агрегатов) в нужном направлении с большой энергией. Для совершения при этом работы необходимо перевести процесс вибрации в нужный колебательный режим, установив необходимый вид управляющих процессов на исполнительные подсистемы, обеспечив заданные технические требования к выполняемым технологическим процессам.

Объекты и методы

Анализ и синтез исполнительных подсистем сельскохозяйственных машин с частотным управлением их рабочими процессами позволяет определить целенаправленность структуры, допустимые частотные интервалы и вид необходимых управляющих воздействий на них [1].

В работах Н.М. Беспамятновой рассмотрены процессы преобразования энергии агрегатов в энергию для преобразования почвы в заданное состояние [2]. Так, на произведение работы по преобразованию, например, почвы из исходного состояния в заданное согласно законам термодинамики необходимо определенное количество энергии ε 1 , причем с определенной скоростью ее поступления. Почва способна поглощать полученную энергию со скоростью х , которая зависит от ее реологических свойств. Поэтому реальный темп подачи энергии к почве Δ зависит от перечисленных характеристик.

Соотношения между перечисленными характеристиками в функциях оператора преобразования Лапласа ( S ) следующие:

'А ( S ) = д ( S ) - х ( S ) е ( S ) = h ( S ) - h i ( S )

^< h ( S ) = W 2 (S ) А ( S ) _ _M ( S ) = W 1 ( S ) _£ ( S )

где h – заданный уровень глубины хода рабочего органа, м; h 1 – реальный уровень глубины обработки почвы, м; ε – дефицит энергии для преобразования пласта в заданное состояние, Дж; μ – необходимый темп поступления энергии (поле скоростей); W 1 – передаточная функция процесса преобразования почвы; х – темп поглощения энергии почвой; Δ – темп подачи энергии к почве.

Условия А ( S ) = д ( S ) - х ( S ) , или А ( S ) = W 1 ( S) e (S ) - х ( S ) - есть условия оптимального соотношения количества энергии, поступающей в почву от рабочего органа и поглощаемого (потребляемого) почвой для ее преобразования в заданное состояние. Оптимальное количество энергии (дефицит) записано во втором уравнении.

Возможны три возможных варианта относительно μ:

Һ 1 ( S ) = h -1   I х , где Т = — - постоянная времени, b < 1;

I b)            b

– в случае дефицита поступления энергии для преобразования пласта получается устойчивый апериодический процесс, который отличается от заданного уровня на величину Г 1 1 _х , т.е.

I ь )

реализуется неустраняемый брак;

• - если добавить темп поступления энергии выше его дефицита, то Һ 1 ( S ) = lim Һ 1 ( S ) = h , в

х ^ 0

этом случае в системе будут иметь место незатухающие колебания на границе устойчивости. Такой режим характерен для консервативного звена;

– в оптимальном случае темп приращения энергии в почве пропорционален его дефициту;

4 ® ^

² ® 2

2                  2 \

®х  ®ц k   ®0

при — > а появляется апериодический процесс, при 111 /а возникает колебательный зату-( b ) "                                                  I b) х и хающий процесс.

Используя представленную теорию процесса формирования глубины обработки почвы на заданном уровне, можно в реальных условиях оценивать полученные результаты при разработке новых механизмов. Для этого достаточно выявить вид передаточной функции спроектированного рабочего органа и сопоставить его с перечисленными вариантами.

Устойчивое функционирование разработанной исполнительной подсистемы определяется с помощью метода структурных исследований динамического состояния их взаимодействия. Метод основан на известном положении, что нестационарные колебания параметрически возбуждаемых систем представляют нетривиальные решения вариационной системы с центром, соответствующим особым решениям систем, и предполагает отыскание зон частотных соотношений возмущающих (подаваемых извне) и собственных частот колебаний (истечение, крошение и др. процессы), обеспечивающих их устойчивое функционирование. Стационарными колебаниями следует считать случай (центр системы) при отсутствии перемещений, а при Z ₁ = Z ₀ + ∆ – система перемещается и может выйти за допустимый предел.

В зависимости от вида показателя динамической устойчивости m у нестационарных колебаний при Z ≠ 0 могут быть три случая:

• –    при k = 1с^–1 – технологический процесс в системе устойчивый и затухающий в до- и зарезонансных режимах;

2ω

• –    при m 〈- ^λ – технологический процесс неустойчив и неуправляем;

ω 0 ²

2 ω ²

• –    при m ≥ - ^λ – технологический процесс неустойчив в определенном диапазоне и ω 0 ²

может быть управляем на его границах.

На основе теории управления динамическими состояниями подсистем алгоритм исследования колебательных процессов в почвообрабатывающих и посевных машинах включает [2]:

• –    определение в каждой подсистеме в соответствии с целью процесса центра вариационной системы (центр бифуркации, особая точка) и чаще всего – это значение агротехнических требований с допустимыми диапазонами;

• –    нахождение теоретического показателя динамической устойчивости заданных показателей процесса и желательности его протекания в одной из зон устойчивости;

• –    установление реального (экспериментального) показателя устойчивости процесса и его положения в реальной зоне устойчивости;

• –    определение запаса устойчивости реального процесса и необходимости изменения возбуждаемой частоты процесса ω λ . В теории регулирования реальный процесс обычно переводят в до- или зарезонансный режимы.

Выбор соответствующей структуры технической системы и ее функционирования в оптимальных режимах нами рассматривается как процесс адаптации выполняемого технологического процесса к заданному состоянию с точки зрения теории автоматического регулирования. Как известно, такую задачу реализуют двумя способами: либо текущим изменением параметров объекта (конструктивного элемента), либо подключением системы управления.

Работа технологической машины и орудия обусловлены созданием определенного динамического состояния исполнительной подсистемы. Согласно [2] для таких систем необходимо установить критерий устойчивости ( m общ ) в зависимости от поставленной задачи. В частности, для почвообрабатывающих агрегатов он имеет вид

4ωλ k mобщ =                          〈

ω2    ω      ω2

λ+ λ + λ k   ω01 + ω02  ω01 + ω02

-

2 ω ²

₂ ^λ ₂ , при k = 1 с^–1, ω ₀₁ + ω ₀₂

где m общ – параметр устойчивости; ω λ – частота внешних колебаний, подающихся на систему, Гц; ω 0 – собственная частота колебаний элементов подсистемы, Гц; k – размерный коэффициент.

Вынужденная частота колебаний ω λ , поступающая на исполнительную подсистему, включает сумму частот воздействий: элементов агрегата, внешних условий на рабочий орган, трактора, рамы сеялки, пласта почвы. Исследованиями [2] установлено, что значение ω 0 в исполнительных подсистемах агрегатах находится в интервале 5–7 Гц, ω 0 1 – 5–6 Гц, ω 02 – 15– 20 Гц. Более того, именно в диапазоне ω λ – 1–4 Гц возникают резонансные явления в подсистемах глубины хода сошников, при этом существенно нарушается равномерность их хода. Согласно теории автоматического управления режим работы исполнительной подсистемы необходимо обеспечивать в до- или послерезонансном режиме.

Область существования режимов работы почвообрабатывающих орудий должна нахо- диться в зоне отрицательных значений, так как при этом движение системы устойчиво, не превышает собственных колебаний; технологический процесс в системе также устойчивый и затухающий в до- и зарезонансных режимах. Для повышения устойчивости глубины хода рабочих органов (на основе представленной методологии анализа и синтеза исполнительных подсистем сельскохозяйственных машин с частотным управлением их рабочими процессами) определены общие динамические закономерности совместной работы подсистем, обеспечивающие ограни- ченный устойчивый темп подачи энергии.

Рассмотрим подвеску сошника как колебательную систему первого порядка, то есть с од- ной степенью свободы [3, 4]. Схематично представим подвеску и рассмотрим силы, на нее дей- ствующие (рис.).

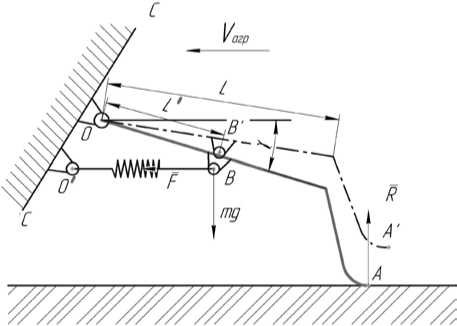
Рис. Схема действия сил на подвеску сошника

Как видно из рисунка, при движении агрегата вперед на подвеску действуют силы: вес механизма – mg (Н), сила упругости пружины – F (Н) и реакция опоры поверхности поля R (Н). В качестве обобщенной координа- ты системы примем угол поворота кулисы подвески сошника относительно горизонтальной плоскости – γ (°).

Для определения закона движения ме- ханизма подвески сошника составим уравнение Лагранжа [5]:

d <дТ) дТ дП I= dt (дү) дү дү ,      (5)

где Т – кинетическая энергия механизма под- вески, Дж; γ – угол поворота кулисы подвески сошника относительно горизонтальной плоскости; П – потенциальная энергия механизма подвески, Дж.

Кинетическая энергия выразится как

• 2     /²

• m ■ l ■ ү

Т = —----, Дж,                          (6)

где m – масса механизма подвески, кг; l – длина кулисы, м; γ^/ – угловая скорость поворота кулисы механизма подвески, с^–1.

Потенциальная энергия механизма подвески определится как сумма

П = П ⁽ Р ) + П ⁽ F ) + П ⁽ R ) , Дж,

где П ⁽ Р ) - потенциальная энергия силы тяжести, Дж; П ⁽ F ) - потенциальная энергия упругости пружины, Дж; П ⁽ R ) - потенциальная энергия реакции поверхности поля, Дж.

Составляющие П(Р), П(F) и П(R) потенциальной энергии рассчитывают по зависимо стям:

П <Р) = - Mg ^L ™^{( ү - ү} 0 ) , Дж,                             (8)

2cos ү

П ( F ) = c ^L '^А ст 2 s ⁱⁿ⁽ Y - Y о ) + c ⁽ L '^АҮ ^- Y о ) Дж, cos ү             2 cos² ү

П ( R ) = R ■ AA 1 = R L ^{Sin( Y} - ^Y 0 ) , Дж,

cos ү где с – коэффициент упругости пружины, Н/м; Δст2 – статическое удлинение пружины, м; γ0 – начальное положение кулисы механизма подвески относительно горизонтальной плоскости, рад.

Подставим выражения (8), (9) и (10) в выражение (7)

_П = - Mg L ^Sin(^ о) + ^cL ^ с ст 2 ^sin( Y - Y о ) + ^{c (} L ') ^{2 Sin} 2 ⁽ Y ^- Y о ) + _R L ^Sin( Y ^- Y о ) , Дж. (11) 2cos y           cos y             2cos² y            cos y

После преобразований и подстановки начальных значений получаем уравнение движения подвески γ = f(t)

Y =

sin2,Yо2cos Yо)

cos kt +

sin2 Y _о 2 cos² ү _о

рад,

где k – частота свободных колебаний механизма подвески, с^–1; t – время, с. Вычисляем частоту свободных колебаний механизма подвески

k

L'

cos L

Yо^

с–1,

где L^/ – расстояние от оси вращения кулисы до точки крепления пружины, м.

По выражению (13) возможно определить угол поворота кулисы механизма подвески γ и отклонение глубины обработки от заданного значения при движении сеялки во время работы. Из анализа данного выражения видно, что, меняя плечо (расстояние от оси вращения кулисы до точки крепления пружины L/), можем существенно влиять на собственную частоту колебания подвески. Также повышая или понижая массу сошника и упругость пружины, можем изменять данную частоту – увеличивая массу сошника – снижать частоту, увеличивая упругость пружины – увеличивать частоту. Следует учитывать обстоятельство: при увеличении частоты при равной массе сошника – уменьшается амплитуда, тем самым снижается неравномерность распределения семян по глубине.

Результаты исследований

Проведем расчет частоты и амплитуды колебаний нашей сошниковой группы для определения неравномерности распределения семян по глубине в зависимости от частоты и амплитуды колебания сошниковой группы.

Воспользуемся формулой (13) для расчета амплитуды и частоты предлагаемой подвески сошника, при этом заданные параметры:

• –    расстояние от оси вращения кулисы до точки крепления пружины, L^/ = 0,5 м;

• –    длина кулисы до точки крепления сошника, L = 1,0 м;

• –    коэффициент упругости пружины, с = 600 Н/м;

• –    вес сошника, М = 50 Н.

Полученные значения внесем в табл. 1, дополнительно проведем расчет угла поворота кулисы механизма подвески γ и отклонение глубины обработки от заданного значения при движении сеялки во время работы S , а также получаемую при этом равномерность распределения семян по глубине К с .

Анализ табл. 1 позволяет сделать вывод о том, что при существующей конструкции сошниковой группы частота свободных колебаний k равна 3 с–1, но, как было сказано выше, в диапазоне ωλ – 1–4 Гц возникают резонансные явления в подсистемах глубины хода сошников, существенно нарушается равномерность их хода, что подтверждается равномерностью распределения семян по глубине Кс. Исходя из этого снижать собственную частоту колебаний k или ω0 сошников нереально и неэкономично (слишком большая масса сошника увеличит расход топлива), наиболее эффективно повышать собственную частоту колебательной системы путем увеличения жесткости пружины, а также снижать частоту ωλ внешних нагрузок, в частности, использовать динамические частотные ограничители. Поэтому снижение воздействия внешних нагрузок проведем соединения двух сошников на одной кулисе, тем самым увеличив массу колебательной системы (сошника).

Таблица 1

Расчет свободных колебаний колебательной системы сошниковой группы

№ п/п	Масса сошника М , кг	Расстояние от оси вращения кулисы до точки крепления пружины L/ , м	Длина кулисы до точки крепления сошника, L , м	Коэффициент упругости пружины с , Н/м	Частота свободных колебаний механизма подвески k , с–1	Отклонение глубины обработки от заданного значения S , м	Расчетная неравномерность распределения семян по глубине К с
1	5	0,3	0,47	600	3,83	0,010	90,16
2	10	0,3	0,47	600	2,71	0,014	86,08
3	15	0,3	0,47	600	2,21	0,017	82,95
4	20	0,3	0,47	600	1,91	0,020	80,31
5	25	0,3	0,47	600	1,71	0,022	77,99

Далее увеличим жесткость пружины. Расчеты приведены в табл. 2.

Расчет свободных колебаний колебательной системы сошниковой группы

Таблица 2

№ п/п	Масса сошника М , кг	Расстояние от оси вращения кулисы до точки крепления пружины L /, м	Длина кулисы до точки крепления сошника, L , м	Коэффициент упругости пружины с , Н/м	Частота свободных колебаний механизма подвески k , с–1	Отклонение глубины обработки от заданного значения S , м	Расчетная неравномерность распределения семян по глубине К с , %
1	10	0,3	0,47	500	2,47	0,015	84,75
2	10	0,3	0,47	1000	3,49	0,011	89,22
3	10	0,3	0,47	1500	4,28	0,009	91,20
4	10	0,3	0,47	2000	4,94	0,008	92,38
5	10	0,3	0,47	2500	5,53	0,007	93,18

Выводы

Как видно из табл. 2, увеличение жесткости привело к росту частоты свободных колебаний k и повышению равномерности распределения семян по глубине К с . Но при этом возникает проблема удержания сошников на заданной глубине, для этого предлагается применять лыжеобразные ограничители хода сошника.