Моделирование контактного взаимодействия элементов пьезоэлектрического двигателя

Высокие радиотехнические характеристики параболических антенн обусловили их широкое применение в конструкциях космических аппаратов (КА). Для систем мобильной связи, средств метеорологического мониторинга и наблюдения за наземными и космическими объектами требуются спутниковые антенны с большим коэффициентом усиления, обеспе- чивающие прием и передачу высокочастотного широкополосного сигнала и имеющие высокое угловое разрешение. Эти требования могут быть реализованы только при больших размерах апертуры и высокой точности отражающей поверхности (ОП) параболической антенны [1–3]. Увеличение размеров рефлектора при ограниченном объеме головного обтекателя ракеты влечет усложнение конструкций трансформируемых рефлекторов космических аппаратов, что приводит к увеличению веса конструкции и усложняет процесс настройки формы ОП.

Одним из перспективных способов настройки формы ОП рефлектора с высокой точностью является применение в конструкции рефлектора КА энергетически автономных натяжителей вантовых элементов. Автономный на- тяжитель состоит из источника питания, блока управления и прецизионного привода. Широкое применение в технике миниатюрных двигателей определяет появление ряда конкурирующих типов преобразователей энергии. Наиболее применимыми в технике являются электромагнитные двигатели и пьезодвигатели (ПД) [4; 5]. Недостатки каждого из типов преобразователей энергии подробно рассмотрены в [6].

ПД обладают рядом преимуществ перед электромагнитными двигателями, что определяет эффективность применения ПД в миниатюрных приводах и устройствах. Для реализации больших линейных перемещений разрабатывают ПД с пошаговым режимом работы. Проблема состоит в том, что в пошаговом режиме работы энергетические параметры ПД резко снижаются.

Цель исследования состояла в разработке математической модели контактного взаимодействия элементов конструкции ПД типа «Захват» для эффективного проектирования подобного типа конструкций.

Описание конструкции ПД типа «Захват» представлено в [6–8]. Особенностью ПД типа «Захват» от ПД других конструкций заключается в наличии контактной пары «захват – шток». При организации угла наклона между толкателем с захватом и штоком захват одной гранью упирается в шток и упруго деформирует его. При этом шток фиксируется захватом. Данный контакт обладает существенным значением силы трения F_{fr 1}, которая позволяет удерживать и преодолевать значительные силы нагрузки вплоть до разрушения корпуса ПД. Перемещение захвата относительно штока в сторону нагрузки ограничивается силой трения F_{fr 2}, которое много меньше F_{fr 1}. Эта особенность данного контакта позволяет организовать пошаговый режим движения штока вместе с нагрузкой. Вопрос моделирования пошагового режима работы ПД при контактном взаимодействии элементов конструкции ПД с учетом сил трения рассмотрен в этой статье.

1. Постановка задачи

Рассмотрим некоторый ПД Ω, представленный набором областей Ω _j = Ω _pk ; k = 1, 2, …, N_p ; j = k со свойствами пьезоэлектрических материалов и набором областей Ω _j = Ω _em ; m = 1, 2, …, N_e ; j = N_p + m со свойствами упругих материалов. Считаем, что физико-механические процессы, происходящие в средах Ω _pk и Ω _em можно адекватно описать в рамках теорий электроупругости и упругости. Пусть Г = ∂Ω – граница области Ω; n = n ( x ) – вектор внешней единичной нормали к Г ( x ∈ Г ).

Для сред Ω _j = Ω _em с чисто упругими свойствами считаем, что состояние среды определя-

ется вектор-функцией перемещений u = u ( x , t ).

Тогда уравнения движения среды имеет вид:

P uittt + ^a d P uitt - ° yj = fi ,             (1)

где u_i , σ _ij – компоненты вектора перемещения и второго тензора напряжений Пиолы-Кирхгофа; α _d – первый коэффициент демпфирования по Релею (инерционный коэффициент); ρ = ρ( x ) – плотность материала; f_i = f ( x_i , t ), при i = 1, 2, 3 – массовые силы.

Связь деформаций и перемещений рассматривается в виде:

⁸ ij =

1 1 du  Su

--L + _L

2 ^S r_y   9Xj

= 2⁽ u i , j ⁺ u j , i )’

где ε _ij – компоненты тензора деформаций.

Для моделирования механического поведения в напряженном состоянии используется закон Гука:

a j = Ж j + 2^ _y,            (3)

0 = 811 + 8 22 + 8 33 = divu, где δij – символ Кронекера; μ, λ – параметры Ламе.

Для пьезоэлектрической среды Ω _j = Ω _pk считаем, что состояние среды определяется кроме вектор-функцией перемещений u = u ( x , t ) также и скалярной функцией электрического потенциала φ = φ( x , t ). Связь деформаций и перемещений рассматривается, как выражение (2), связь напряженности электрического поля E и потенциала φ рассматривается в виде:

E .--^, -         (4)

d x

Для пьезоэлектрической среды в линейном приближении существует линейная связь между тензором деформаций ε и вектором напряженности электрического поля E с тензором напряжений σ и вектором электрической индукции D . Эти зависимости носят название определяющих соотношений и имеют следующий вид:

^G у = c jjki ( ⁸ ki ⁺ P d ’ ⁸ ki , t ) ^— e kij E k ,           ⁽⁵⁾

D i = e iki ⁸ ki + ⁸ ik E k ,                 (6)

где cE_kl , e_{i kl} , г S_ik - материальные константы, характеризующие, соответственно, упругие, пьезоэлектрические и диэлектрические свойства материала тела; β _d – второй коэффициент демпфирования по Релею (конструкционный коэффициент) [9].

Для пьезоэлектрического тела уравнения движения будут иметь вид, как для упругого тела (1).

В силу того, что скорости упругих и электромагнитных волн отличаются на порядки, а

пьезоэлектрические среды являются диэлектриками, можно принять уравнение приближения квазиэлектростатики вида:

D =ⁿ ^ ,

где σΩ – объемная плотность электрических зарядов, причем σΩ = 0.

Подставляя в (1) и (7) определяющие соотношения (5) и (6) и формулы (2) и (4), получаем итоговую систему дифференциальных уравнений линейной электроупругости относительно функций u и φ:

P U I , tt + ^a d p M i , tt

⁽ C Ea ( ^u k , l + p d u k , It ) - e kij Ф , k X. j = fi , (8)

-

• ⁽ e iki u k , i - ^e SЪ ) , i =^_n .               (9)

Граничные условия подразделяются на механические и электрические.

Для формулировки механических граничных условий предположим, что граница Г разбивается на два участка Г_u и Г _σ, на которых задаются, соответственно, векторы перемещений u_Г и напряжений p_Г .

Тогда механические граничные условия для закрепленных граней тела:

u = u_r , u_r = 0, x e Г_и ,           (10)

Так как пьезопакет предварительно нагружен, то справедливо выражение:

p = n -o , p = P r , x e Г т ,          ⁽¹¹⁾

где p = n ^* ∙ σ – трехмерный вектор напряжений на площадке с нормалью n , при этом внешние воздействия u_Г и p_Г зависят от пространственных переменных x и времени t [9].

Для учета поведения материалов при контактном взаимодействии элементов ПД введем дополнительные механические граничные условия. Возьмем две области с упругими свойствами Ω _en и Ω _{e ( n + 1)}, причем область Ω _en включает область Ω e ( n + 1) , Ω en ∈ Ω em , Ω e ( n + 1) ∈ Ω em , n <  m . Контактное взаимодействие элементов ПД характеризуется одновременным действием тангенциальных F_x и нормальных F_N сил.

Условие схватывания двух тел имеет вид: τ ≤ μσ, где τ – тангенциальное напряжение, σ – нормальное напряжение, μ – коэффициент трения.

Зона контакта разделяется на две зоны: зона схватывания (область Ω _{e ( n + 1)}), зона проскальзывания (область Ω _en без Ω e _{( n + 1)}, Ω _en \Ω _{e ( n + 1)}). Схватывание внутри зоны контакта означает, что в этой области смещения постоянны [10]:

u i ( x ) = const при x E Q e _{( n + 1)} .          (12)

В области проскальзывания действует закон трения Кулона:

• ^T = цст ( x , t ) при x E n en \ Q e ₍ n + 1) .       (13)

Том 3

Для задания электрических граничных условий будем считать, что существует независимое разбиение границы Г : Г = Г _φ + Г_D .

На границе Г _φ нанесены электроды, которые питаются генератором напряжения с выходным потенциалом V ( t ), то есть:

ф = Фг , Фг = V(t), x е Г,,

На границе пьезоэлектрического материала Г_D , где нет электродов, задается поверхностная плотность электрических зарядов σ _Г = σ _Г ( x , t ):

n * • D = -^ Г, су Г = 0, x e rD,(15)

Начальные условия: при t = 0 поле перемещений u ₀ и скоростей v ₀ предполагается заданным:

u (x ,0) = u 0( x),

• u, t (x ,0) = Vq( x),(17)

• 2.    Построение модели

  • 2.1    Моделирование конструкционного узла захват-толкатель.

где u ₀( x ) - начальное положение тела, v ₀ ( x ) - начальная скорость.

Таким образом, постановка задачи для системы ПД включает в себя систему дифференциальных уравнений (1)–(9), граничные условия (10)–(15) и начальные условия (16) и (17) [11].

При моделировании конструкционного узла захват-толкатель экспериментально определялась жесткость этого узла.

Определение жесткости соединения элементов захвата и толкателя в конструкции пьезоэлектрического привода типа «Захват» проводилось с помощью настольной системы для микроиспытаний INSTRON MicroTester 5948 (USA).

При испытаниях пьезоэлектрический привод типа «Захват» фиксировался на предметном столике настольной системы в вертикальном и горизонтальном положении, и к захвату подводился индентор. Индентор перемещался со скоростью 0,5 мм/мин, и при этом фиксировался уровень нагрузки и величина перемещения. Ограничение по нагрузке составляло 10 Н.

На рис. 1 приведены результаты экспериментальных исследований по определению жесткости соединения элементов захвата и толкателя. Таким образом, при вертикальном расположении ПД прогиб соединения захвата и толкателя под действием вертикальной нагрузки составляет 0,025 мм, а при горизонтальном расположении ПД прогиб составляет 0,05 мм.

Конструкционный узел захват-толкатель моделировался в виде стержня. Жесткость стержня должна соответствовать полученным экспериментальным данным. Для определения геометри- ческих размеров стержня использовалось соотношение по определению прогиба стержня из [12]:

y (l) = -( F - l3)/(3 - E - Jx) - (1+ X), где y(l) – наибольший прогиб стержня, м; l – длина стержня, м; F – изгибающая сила, Н; E – модуль Юнга материала стержня, Па; Jx = b • h3/12 - момент инерции сечения стержня; b – толщина сечения стержня, м; h – высота сечения стержня, м; Z = k(1+v)h2/212 - коэффициент приращения прогиба при учете деформации сдвига; k – безразмерный коэффициент сдвига, зависящий от формы поперечного сечения; ν – коэффициент Пуассона материала стержня.

k = 800 Н/м. Жесткость упругой связи определена в соответствии с методикой, представленной в [14].

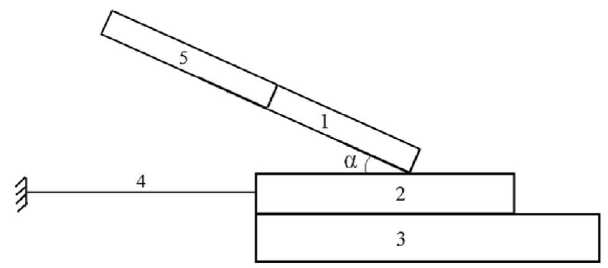
Рис. 2. Расчетная геометрическая модель

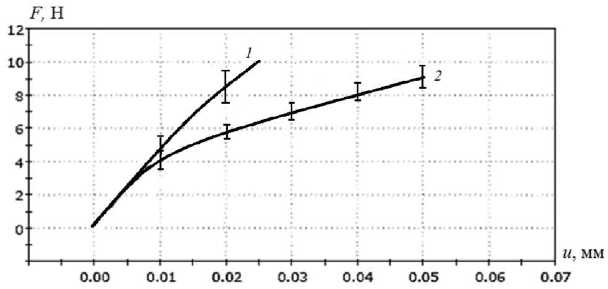
Рис. 1. График зависимости величины прогиба захвата от величины нагрузки: 1 – вертикальное расположение ПД;

2 – горизонтальное расположение ПД

По результатам расчета подобраны оптимальные геометрические размеры стержня, которые будут использоваться в моделировании: h = 0,0015 м, b = 0,003 м, l = 0,0137 м.

• 2.2    Моделирование контактного взаимодействия захват-шток.

Работоспособность ПД зависит от надежности контактной пары захват-шток. Моделирование напряженно-деформированного состояния элементов ПД при заданных рабочих нагрузках проводилось с использованием программы конечноэлементного моделирования ANSYS.

На рис. 2 представлена расчетная геометрическая модель контактной пары захват-шток, которая рассматривается в двумерной постановке. Поскольку в конструкции ПД предусмотрено, что шток проходит в отверстие захвата, ограничен этим отверстием и не имеет возможности смещаться в сторону, то достаточно рассмотреть эту задачу в двумерной постановке. Геометрическая модель состоит из пяти элементов: захват (1), шток (2), корпус (3), вант рефлектора (4) и пьезопакет АПМ 2-22 (5) [13]. В задаче учитывается корпус, потому что необходимо учесть силу трения штока о корпус. Захват к поверхности штока располагается под углом α. Взаимодействие вант с другими элементами конструкции рефлектора моделируется упругой связью с жесткостью

На основе геометрической модели строилась конечно-элементная модель (КЭМ). Для наглядного отображения напряженно-деформированного состояния (НДС) элементов конструкции при их нагружении необходимо в местах наиболее вероятных максимальных напряжений уменьшить размеры элементов. В рассматриваемом случае это зона контакта захват-шток. На рис. 3 представлена КЭМ и продемонстрировано уменьшение элементов в зоне вероятных максимальных напряжений.

(а)                            (б)

Рис. 3. Конечно-элементная модель (а) и зона захват-шток (б)

Количество элементов в представленной КЭМ составляет 7094. Для расчетов использовался двумерный элемент объемного НДС Plane42. Для захвата и штока был выбран материал сталь, для корпуса – алюминий, для пьезопакета – ЦТС46. Коэффициент трения сталь/сталь µ равен 0,2; коэффициент трения алюминий/сталь µ равен 0,1. Свойства материала представлены в табл. 1. Данные по пьезокерамике взяты из [11], по остальным материалам – справочные.

Таблица 1

Свойства материалов

Материал	Плотность, кг/м3	Модуль упругости, Па	Коэффициент Пуассона
Сталь	7800	2,1·1011	0,29
Алюминий	2700	7·1010	0,34

В расчетной модели учитываются две пары контактов: захват-шток (тип: узел-поверхность) и шток-корпус (тип: поверхность-поверхность).

Граничные условия в расчетной модели: корпус ПД, вант и левая грань пьезопакета жестко закреплены по всем направлениям (рис. 3).

Том 3

• 2.2.1    Определение НДС в зоне контактного взаимодействия.

• 2.2.2    Переходный процесс пуска ПД.

В конструкции ПД захват упирается гранью в поверхность штока, тем самым прижимая шток к поверхности корпуса. От угла наклона захвата к поверхности штока α будет зависеть величина перемещения штока и максимальная интенсивность напряжений в зоне контакта захвата и штока. При подаче управляющего сигнала на пьезопакет, пьезопакет удлиняется и давит на захват. При этом захват контактирует со штоком и перемещает его.

В табл. 2 представлены результаты моде- ²²⁶ лирования величины перемещения штока при перемещении захвата на заданную величину. Варьировался угол наклона захвата к поверхности штока α. Совместно с величиной перемещения в каждом рассмотренном случае оценивалась интенсивность напряжений в области контакта захвата и штока.

Таблица 2

Результаты моделирования

Угол наклона α, º	Перемещения по оси X, ×10–4 м	Максимальная интенсивность напряжений σ, ГПа
30	0,263	7,16
20	0,285	4,76
15	0,291	3,61
12	0,293	2,83
10	0,294	2,29
9	0,294	2,02
8	0,294	1,77
6	0,294	1,3
5	0,294	1,1
4	0,293	0,851
3	0,292	0,619
2	0,292	0,426
1	0,291	0,206

Анализ результатов моделирования НДС конструкции ПД типа «Захват» показал, что при увеличении угла наклона α перемещение штока уменьшается. При увеличении угла наклона возрастает вертикальная составляющая силы нагрузки, а, следовательно, и сила трения, что влечет уменьшение величины перемещения штока. Но и при уменьшении угла наклона α есть момент, когда вертикальная (прижимная) составляющая силы нагрузки становится очень маленькой и захват начинает проскальзывать. Такой процесс наблюдается при угле наклона α ≤ 4°. По результатам моделирования определен максимальный порог величины перемещения штока X , равный 0,294∙10^–4 м при угле наклона 10° ≥ α ≥ 5°. По результатам оценки максимума интенсивности напряжения в каждом из этих случаев, наиболее оптимальным является расчетный случай при угле наклона α = 5°, при этом σ = 1,1 ГПа.

Расчет переходного процесса пуска ПД проходил в два этапа:

• 1)    Вертикальный прижим захвата к штоку, где варьировалась величина предварительного поджатия. Таким образом, имитируется положение захвата в конструкции ПД при фиксации штока.

• 2)    Подача на пьезопакет управляющего пилообразного сигнала, где варьировалась частота сигнала. Время подачи сигнала составляло 1 с.

В расчетной модели на пьезопакет ПД подавалось напряжение в виде пилообразного сигнала. Пьезопакет преобразовывал электрическую энергию в механические колебания на основе свойств материала пьезокерамики, заложенных в модели. На рис. 4 представлен график зависимости перемещения свободной от закрепления границы пье- зопакета от времени в одном из рассмотренных случаев.

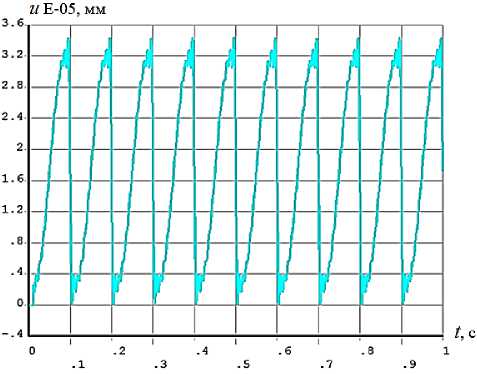
Рис. 4. Перемещение на свободной от закрепления границе пьезопакета

В результате решения получены зависимости величины перемещения штока от времени. На рис. 5 приведен график перемещения штока при силе поджатия захвата F = 10 Н и частоте управляющего сигнала f = 30 Гц.

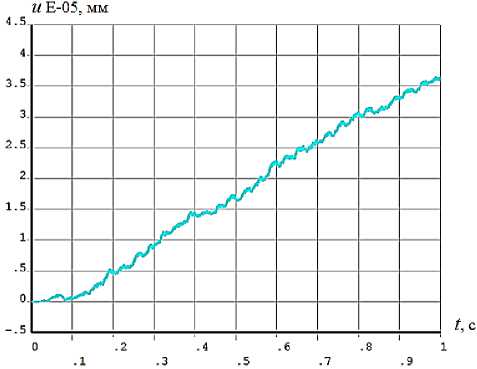
Рис. 5. Результаты расчета. Перемещение штока

Результаты моделирования взаимодействия элементов конструкции привода представлены в табл. 3. Выявлено влияние выбранных параметров режима работы (силы поджатия захвата F и частоты управляющего сигнала f ) на максимальное перемещение штока.

Таблица 3

Влияние выбранных параметров режима на перемещение штока

Частота сигнала, Гц	Сила поджатия, Н	Максимальное перемещение штока, ×10–6 м	Скорость перемещения штока, мм/мин
10	1,5	4,8	0,288
	5	5,9	0,354
	10	6,6	0,396
20	1,5	7,3	0,438
	5	12,9	0,774
	10	13,5	0,81
30	1,5	18	1,08
	5	29	1,776
	10	30,6	1,83

Для определения достоверности предложенной конечно-элементной модели проведено сравнение теоретических расчетов и экспериментальных данных.

Задавались одинаковые условия: амплитуда напряжения U = 100 В, частота сигнала f = 30 Гц, сила поджатия захвата к штоку F = 10 H.

Эксперимент проводился на экспериментальном стенде с нагрузкой в виде упругой связи, где варьировалась сила упругого сопротивления от 0 до 12 Н. Работа ПД без нагрузки (холостой ход) проходила при скорости перемещения штока V = 6,6 мм/мин. С увеличением силы упругого сопротивления до Fnag = 10 Н скорость штока уменьшалась линейно до 0,15 мм/мин, при Fnag = 12 Н скорость штока снизилась до нуля (режим короткого замыкания).

По результатам моделирования определено, что скорость перемещения штока равна V = 1,83 мм/мин и сила упругого сопротивления при данной скорости составляет F_nag = 6,61 Н. Расхождение результатов моделирования с экспериментальными данными составляет 6 %.

Полученные результаты моделирования наглядно демонстрируют достоверность данного подхода по подбору материалов для изготовления конструкции ПД, выбору оптимальных режимов работы ПД.

Заключение

По результатам проведенного исследования разработана конечно-элементная модель ПД, учитывающая особенности контактного и электроупру-гого деформирования. Модель учитывает характер внешней нагрузки на ПД и может использоваться для проектирования энергетически автономных натяжителей антенных рефлекторов КА.

Разработан алгоритм решения нелинейного динамического контактного взаимодействия элементов ПД для всех режимов работы, включая переходный процесс при пуске системы. Исследовано влияние параметров режима работы ПД на величину перемещения штока.