Моделирование координатных измерений геометрических параметров формы и расположения сложных профилей лопаток компрессора ГТД

ний, однако для ряда задач он является предпочтительным. К таким задачам относится контроль поверхностей имеющих высокую отражательную способность, например лопаток компрессора изготовленных из хромоникелевых сплавов с малой шероховатостью (Ra 0,63 … 0,32 мкм). Контроль таких лопаток может осуществляться с использованием трех осевых координатно-измерительных машин, оснащенных триггерным или сканирующим датчиками с измерительным наконечником сферической формы.

Современные координатно-измерительные машины имеют сравнительно малую инструментальную погрешность измерений, находящуюся в диапазоне от 1 до 7 мкм, определяемую измеряемыми габаритами. Однако, как показывает практика их использования, результирующая погрешность измерений может быть больше. Важной метрологической и производственной задачей является определение фактической погрешности измерений.

Целью работы является разработка методики моделирования процесса координатных измерений сложного профиля для оценки погрешностей измерения геометрических параметров формы и расположения профиля.

Действительная погрешность и производительность измерений зависит от множества факторов [1]:

• 1.    инструментальных погрешностей средства измерения;

• 2.    используемой методики выполнения измерений;

• 3.    погрешностями формы и расположения измеряемых поверхностей деталей;

• 4.    используемыми алгоритмами обработки измеренных точек;

• 5.    внешними факторами.

Поддающимися управлению с целью снижения погрешностей измерений являются факторы: 2 – используемая методика выполнения измерений, 4 – используемые алгоритмы обработки измеренных точек и 5 – внешние факторы. Рассмотрим каждый из них.

К внешним влияющим факторам относится температура, влажность и засоренность окружающей среды. Они могут поддерживаться на необходимом уровне, либо компенсироваться, например включением термокомпенсации. Методика выполнения измерений представляет собой последовательность выполнения измерений, которая включает в себя: черновое (стартовое) и чистовое базирование посредством измерения базовых поверхностей, последовательность и способ измерения точек на остальных поверхностях, используемые алгоритмы обработки измеренной информации, способ построения и расчета геометрических параметров из известных измеренных параметров, порядок представления информации в протоколе. Особое значение имеют используемые алгоритмы обработки измеренных точек. Существует несколько типов используемых алгоритмов обработки измеренных точек. Например, аппроксимация измеряемых координат точек базовых поверхностей, к которым относятся плоскости, цилиндрические поверхности, зачастую осуществляется методом наименьших квадратов. При измерении сложных поверхностей или профилей измерительным наконечником сферической формы возникает проблема компенсации радиуса. В процессе измерения известен центр измерительного наконечника в момент касания поверхности, а действительная точка получается расчетным путем. Существует несколько способов компенсации радиуса измерительного наконечника. Наиболее распространенным является расчет точки качания исходя из известных координат и вектора нормали в ней номинальной измеряемой точки.

При таком способе компенсации будет возникать дополнительная погрешность измерения, вызванная отклонением направления нормали реального профиля в измеряемой точке от номинального направления (ошибка компенсации радиуса щупа, рис. 1).

Эту ошибку в случае использования сферического наконечника можно найти по формуле [2]:

A = R • (1 - cos(a)),       (1)

где R – радиус измерительного наконечника, α – угол между расчетной (номинальной) и реальной нормалями в измеряемой точке (рис. 1).

Приведенная модель не позволяет оценить погрешность измерения геометрических параметров отклонения и формы профиля. Для их совместной оценки осуществлена разработка методики моделирования, воспроизводящая процесс координатных измерений (рис. 2).

Методика моделирования включает в себя последовательность этапов. Опишем подробно каждый из этапов.

На первом этапе задается план экспериментов. Элементы плана содержат информацию об имитируемых значениях отклонений формы и расположений профилей.

На втором этапе осуществляется загрузка координат точек номинального профиля P_í и моделируются параметры отклонения формы (Δ формы ) и расположения (Δ расп ). Погрешность

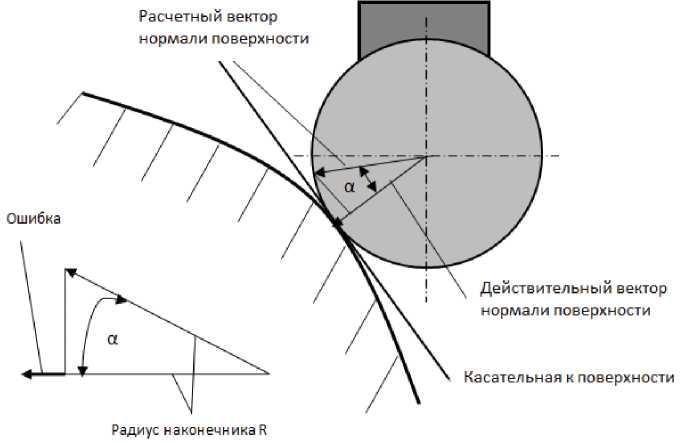
Рис. 1. Оценка погрешности D, вызванной несовпадением номинального и реального направления нормали к поверхности

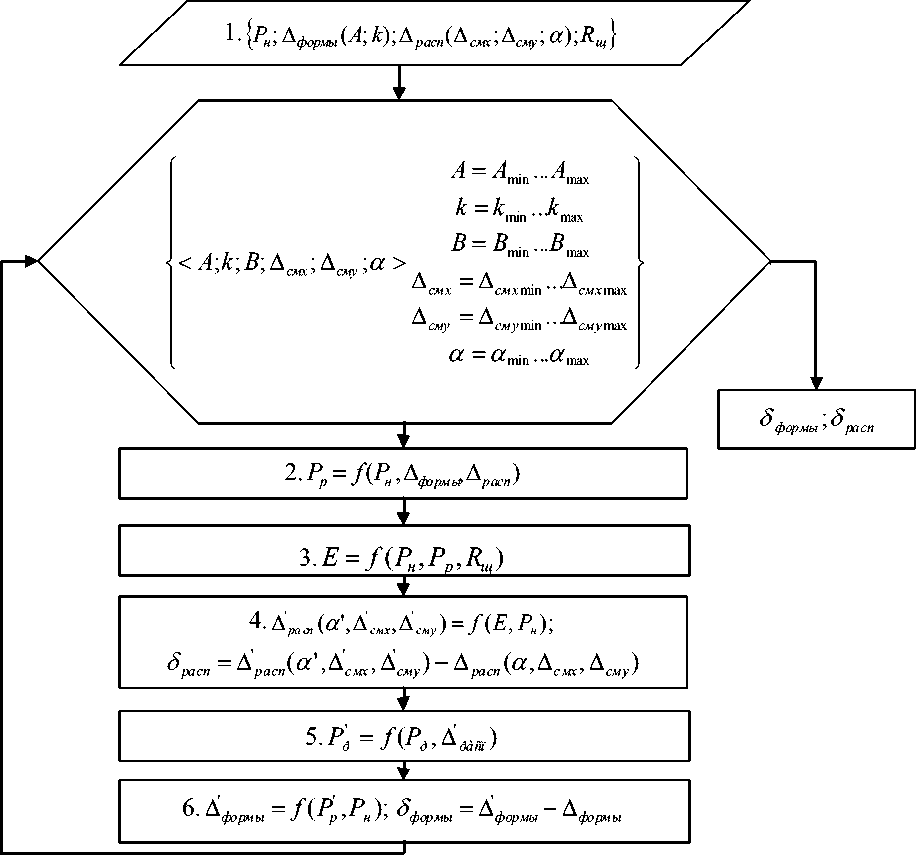
Рис. 2. Блок-схема программы исследования погрешности координатных измерений

формы профиля моделируется как включающая в себя гармоническую и случайную составляющие, следующим образом:

Окончательно координаты точки реального профиля находятся из координат точки номинального профиля по формуле:

A

формы

^A гарм + ^A случ ,

Р_р = Р_н + A рн

формы

^{+ A} расп ,

где A _гарм - гармоническая составляющая погрешности формы профиля точек профиля, которая находится по формуле:

^A гарм = А • COS(( x I k ■ 2 • Я )/L пр ) ,    (3)

где А – амплитуда гармонической составляющей; k – частота гармонической погрешности; L_пр – опорная длина профиля по оси Х; x – координата точки Р _н ;

Aслуч — случайная составляющая погрешности формы профиля точек профиля, имитирующая инструментальную погрешность измери- тельного средства;

A расп — погрешность расположения профиля, состоящая из 3 параметров: угла поворота про- филя а и смещения по координатным осям

A

см . х

, A

см . у

где P _p – координаты точек реального (измеряемого) профиля.

Непрерывное представление имитируемого и номинального профиля осуществляется интерполяцией соответствующих массивов координат точек профилей с использованием NURBS сплайна 3-й степени [3, 4].

На третьем этапе осуществляется моделирование касания измерительного наконечника об имитируемый профиль, который является измеряемым. В процессе моделирования определяются координаты точек касания щупа и профиля, и координаты центров щупа. Для нахождения этих основных координат разработан улучшенный алгоритм, как альтернатива алгоритму, приведенному в [5]. Определяемые и задаваемые параметры приведены на рис. 3.

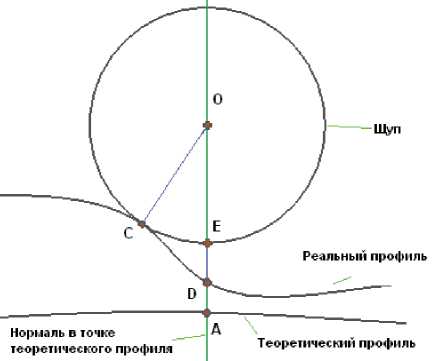
Рис. 3. Схема измерения профиля сложной поверхности:

А – измеряемая точка номинального профиля; D – точка реального профиля, которую пересекает нормаль к точке А; C – точка касания измерительного наконечника и реального профиля; O – центр измерительного наконечника в момент касания поверхности; E – точка, лежащая на пересечении нормали точки А и окружности щупа

На пятом этапе координаты точек имитируемого профиля, корректируются с целью исключения ошибки расположения. При этом определяются координаты имитируемого профиля для оценки погрешности формы:

P p = E • M пр . (7)

На шестом этапе по точкам припасованного профиля P _ð задается сплайн NURBS. После этого вычисляются нормали в точках P_í к номинальному профилю, находятся координаты точек пересечения этих нормалей и припасованного измеренного профиля E _t . Расстояния P . E 1 характеризуют оцененную погрешность формы профиля А ф _ормы . Погрешность найденного отклонения представляет собой массив разностей оцененной и заложенной отклонений формы профиля в точках:

8, формы

а'

формы

^А формы .

Измерение точки профиля осуществляется следующим образом: щуп движется по нормали к измеряемой точке А, расположенной на номинальном профиле. Касается реального профиля в точке С, которая не совпадает с точкой А. На пересечении теоретической нормали и окружности щупа лежит рассчитываемая машиной точка Е, на пересечении теоретической нормали и реального профиля – точка D.

На четвертом этапе осуществляется определение наилучшего совмещения имитируемого (точки E) и номинального(точки Р _н ) профиля. При этом формируются измеренные в ходе моделирования параметры расположения профиля. Полученные параметры расположения профиля используются для вычисления матрицы наилучшего совмещения номинального и измеренного (оцененного) профилей (припасовки), которая выглядит:

M пр

cos a' sin a 0

- sin a cos a о T                                                  . T

A A 1

см . x         см . y

Погрешность измерения отклонения расположения от номинального значения можно охарактеризовать отклонениями между полученными и заданными планом эксперимента углом поворота профиля и смещения по координатным осям:

a—a,

^ расп

смх

-

А смх ,

Полученные значения З _ф ормы и ⁵ расп записываются для каждого набора входных параметров и используются в дальнейшем анализе.

Приведенные этапы реализуются посредством разработанных программных модулей.

Таким образом, для каждого элемента плана эксперимента определяются погрешности измерения отклонения формы и расположения. Разработанная методика будет использоваться для оценки погрешностей измерения геометрических параметров сложных профилей и определения неопределенности результатов измерений, позволяющих распространить их на партию изготавливаемых лопаток.

Первоначально осуществлялось исследование отклонений формы и расположения профилей серийных лопаток на ОАО «КУЗНЕЦОВ» с использованием координатно-измерительной машины DEA Global Performance 07.10.07.

В ходе измерений получены результаты отклонений по форме и расположению. Отклонение расположения приведены на рис. 4 и 5. Рис. 4 содержит вектора отклонений расположений от номинального (нулевого) значения для выборки лопаток по сечениям. Анализируя рисунок можно отметить, что наблюдается тесная корреляция между величинами смещения по оси Xи Y. Чем выше по модулю величина смещения по одной оси, тем выше величина смещения по другой оси.

На рис. 5 приведены значения углового отклонения расположения относительно номинального положения для соответствующих измеренных лопаток.

Измеренное отклонение формы выборочных лопаток приведены на рис. 6.

Результаты измерений показывают, что из-

сму

-

А сму*

меренные детали имеют схожую погрешность

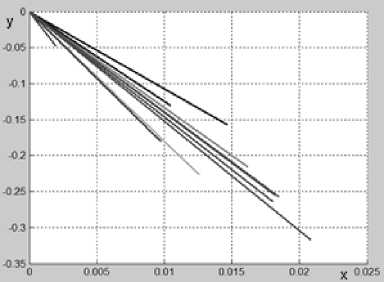
Рис. 4. Результаты измерений линейного отклонения расположения по серии лопаток, мм

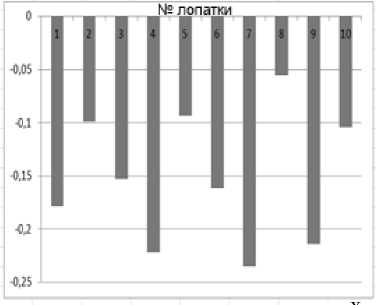
Рис. 5. Результаты измерений отклонений углового отклонения расположения по серии лопаток, град

формы. Наибольшее отклонение формы проверяемых лопаток от формы номинальной детали наблюдается на входной и выходной кромке изделия, в центральной части отклонение незначительное. На основе измерений партии лопаток можно сделать вывод о том, что изготавливаемые лопатки, произведенные по аналогичному технологическому процессу, будут иметь близкое отклонение формы.

Схожесть отклонения формы позволит распространить оценку погрешности измерения с измеренной партии лопаток на все партии лопаток, произведенные по аналогичному технологическому процессу.

На основе проведенных измерений определены граничные условия отклонений формы профиля и разработан план экспериментов по моделированию и определению погрешности измерения (табл. 1).

На основе плана экспериментов осуществлено моделирование процесса измерения с имитируемым отклонением формы и расположения измеряемого профиля. В результате получены следующие зависимости погрешностей измерения. На рис. 7 представлена зависимость погрешности измерения формы профиля от величины амплитуды гармонической составляющей вдоль профиля.

На рис. 8 представлена зависимость погрешности измерения формы профиля от величины частоты гармонической составляющейk.

В ходе экспериментов установлено влияние фактического отклонения расположения имитируемого профиля на погрешность измерения формы профиля. На рис. 9 показана зависимость максимальной оцененной погрешности измерения формы профиля от амплитуды гармонической составляющей.

Анализируя полученные результаты можно отметить, что зависимость погрешности измерения отклонения формы профиля от параметров гармонической составляющей является линейной.

На рис. 10 показана зависимость максимальной оцененной погрешности измерения формы

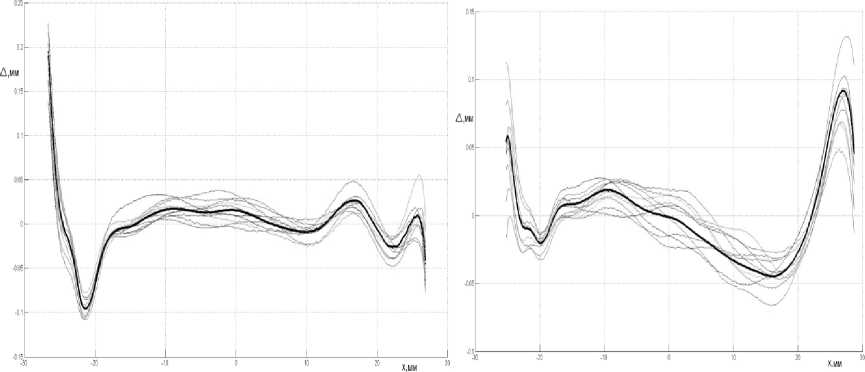
а)                                                    б)

Рис. 6. Отклонение формы для сечения корытца на высоте: а –17 мм, б – 172 мм

Таблица 1. План экспериментов

Се чени е			A, мм		k, ед.
Название	Поверхность	Выс ота, мм	min	max	min	max
K17	корытце	17	0,01	0,25	2,5	18
C17	сп инка	17	0,02	0,25	2	28
K100	корытце	100	0,03	0,20	6	26
C100	сп инка	100	0,01	0,28	3	19
K172	корытце	172	0,01	0,13	4	19
C172	сп инка	172	0,01	0,15	2	16

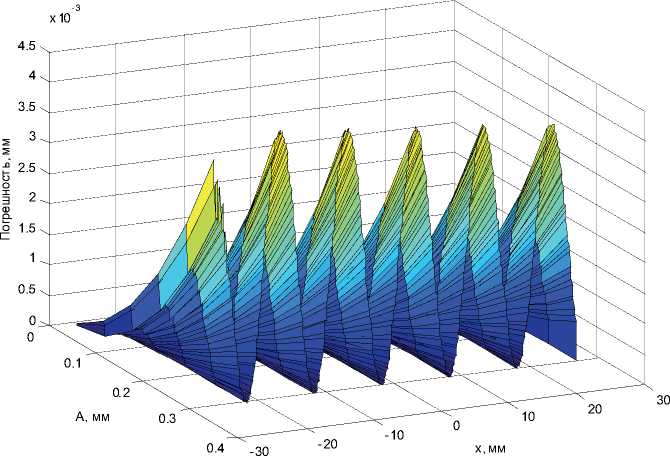
Рис. 7. Зависимость погрешности измерения отклонения формы профиля от величины амплитуды гармонической составляющей вдоль профиля

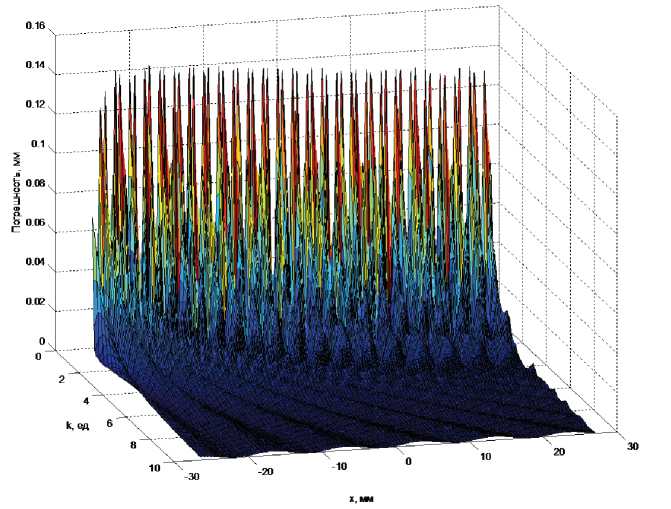
Рис. 8. Зависимость погрешности измерения отклонения формы профиля от величины частоты гармонической составляющей k

А, мм

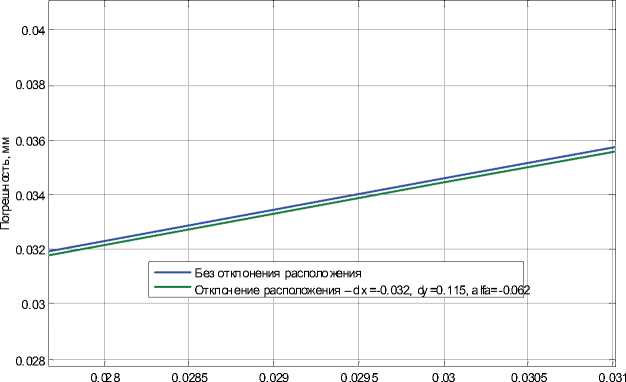
Рис. 9. Зависимость максимальной оцененной погрешностиизмерения формы профиля от амплитуды гармонической составляющей

профиля от величины частоты гармонической составляющей k для различного отклонения расположения.

Погрешность измерения формы вдоль про- филя при имитировании только отклонения фор мы приведена на рис. 11.

Полученные данные позволяют сделать вы вод о том, что зависимость погрешностей изме

0.27

0.26

0.25

0.24

0.23

1 0.22

0.21

0.2

0.1 9

0.1 8

0                5               10               15              20              25               30

k, ед.

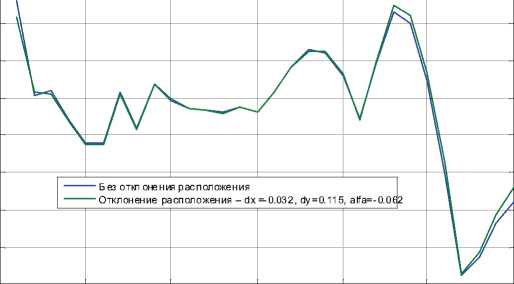
Рис. 10. Зависимость максимального отклонения формы от величины частоты гармонической составляющей k для различного отклонения расположения

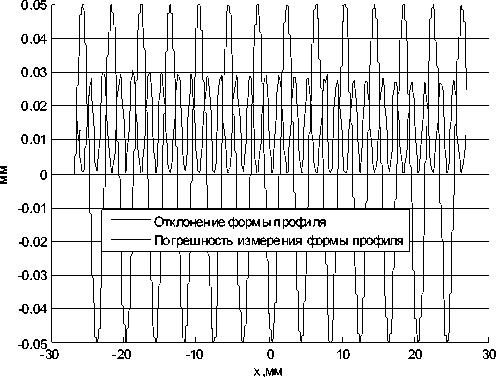
Рис. 11. Погрешность измерения формы вдоль профиля при отсутствии отклонения расположения, при A=0.05, k=2

рений геометрических параметров отклонения расположения и формы профиля существенна, может принимать значительные величины по сравнению с допустимыми погрешностями измерений. Поэтому их нужно принимать во внимание при оценке фактической точности измерений и разработке методик выполнения измерений.