Моделирование корреляции доходности акций в контексте расчета показателя диверсификационного потенциала заданного множества активов

МНОЖЕСТВА АКТИВОВ

Явление кластеризации волатильности временных рядов, в частности кластеризация волатильности доходности активов, отмеченное еще в работах Б. Мандельброта [1], фактически представляется важнейшей предпосылкой в контексте реализации большинства моделей прогнозирования волатильности. Что стоит за явлением кластеризации волатильности и как устроен процесс трансформации кластеризации волатильности доходности отдельно рассматриваемых активов с микроуровня в кластеризацию волатильности рыночной доходности на макроуровне? Гипотеза нашего исследования состоит в том, что показатель динамики диверсификационного потенциала рынка [2] несет в себе информацию, которая может быть полезна для описания названных ранее процессов и явлений.

В статье рассматривается понятие диверсификационного потенциала заданного множества активов, позволяющее, в отличие от существующих подходов на основе рыночных индексов, оценивающих динамику волатильности на макроуровне, определять также относительную важность общих макроэкономических условий функционирования на рынке в целом или в определенном секторе по сравнению с частными инвестиционными параметрами отдельно рассматриваемых активов. Разработана и применена методика расчета индекса диверсификационного потенциала рыночных отраслей и рынка в целом на базе динамики попарных коэффициентов корреляции соответствующих активов. Предложены подходы к моделированию динамики индексов диверсификационного потенциала.

Цель исследования: разработка методики расчета и моделирования показателя диверсификационного потенциала заданного множества активов на основе моделирования корреляции доходности акций.

Задачи исследования:

• 1)    изучить и сравнить подходы к моделированию корреляции доходности акций на основе семейств моделей динамической условной корреляции и реализованной ковариации (корреляции);

• 2)    разработать методику расчета показателя диверсификационного потенциала заданного множества активов;

• 3)    предложить подходы к моделированию динамики индексов диверсификационного потенциала.

Само название этого индекса – диверсификационный потенциал – говорит о том, что его динамика характеризует динамику возможности формировать диверсифицированные портфели на основе заданного множества активов, например рынка акций конкретной страны и т. п. Показатели корреляции между активами меняются во времени, а именно они характеризуют возможность осуществления диверсификации при формировании финансовых портфелей. Если величина попарных корреляций низкая, это создает благоприятные условия для формирования финансовых портфелей. В противном случае, если уровень попарной корреляции между активами стремится к единице, возможности диверсификации (особенно в отсутствие коротких продаж) в экономике практически нет. Это оказывает сильное влияние на поведение как экономических агентов на микроуровне, так и экономических регуляторов и иных финансовых институтов, так как, помимо прочего, речь идет о динамике диверсификационного потенциала целых отраслей экономики и рынка в целом.

Волатильность доходности активов меняется во времени, как и корреляция их доходностей. Причем данные процессы взаимосвязаны. Разработка подходов, позволяющих моделировать динамику волатильности доходности активов с учетом взаимосвязанности финансовых активов, продолжается до сих пор. Так, еще в 1990 г. Т. Боллерслев (T. Bollerslev) предложил модель постоянных условных корреляций (Constant Conditional Correlation, CCC) для использования в многомерных модификациях моделей обобщенной авторегрессионной условной гетероскедастичности при прогнозировании волатильности доходности активов [3]. В дальнейшем, в попытке преодолеть ограничения в виде постоянства коэффициентов попарных корреляций между активами, Р. Энгл (R. Engle) в 2002 г. предложил модель динамических условных корреляций (Dynamic Conditional Correlation, DCC) [4]. В качестве более упрощенного аналога приведенных моделей может выступать многомерная модель экспоненциально взвешенной скользящей средней (Multivariate Exponentially Weighted Moving Average, MEWMA) [5]. Есть и другие модификации моделей, в которых предпринимаются попытки тем или иным способом имплементировать взаимосвязи между величинами волатильности и корреляций между активами в контексте интерпретации наблюдаемых значений и их прогнозирования, такие как относительно более простая ортогональная модель обобщенной авторегрессионной условной гетероскедастичности (Orthogonal GARCH, OGARCH), предложенная в 1994 г. в работе К. Александера и О. Чибумбы (C. Alexander, Au. Chibumba) [6], или, например, BEKK-модель (название состоит из первых букв фамилий создателей: Baba, Engle, Kraft, Kroner), требующая применения более сложных подходов к оценке параметров [7].

Динамика показателей корреляции между активами имеет большое значение не только в контексте определения будущих значений показателей их волатильности, но и в рамках портфельной теории управления финансовыми активами, диверсификации рисков и т. д. Многомерное моделирование волатильности и корреляций доходностей рассматриваемых активов позволяет более полно учитывать имеющуюся на рынке информацию при принятии инвестиционных решений.

Одним из наиболее простых подходов к моделированию многомерной волатильности представляется использование многомерной модели, экспоненциально взвешенной скользящей средней MEWMA (1):

^a t,ij = ^Лa t - 1,i; + ^{(1   Л)y} t - 1,i ^y t - 1,; , M = 1, ■" , ^ ,

• где   o_{t lj} - ковариация между соответствующими активами в момент t ;

• Л - константа, значение которой находится в интервале от 0 до 1;

• y _t _ 1,[ - величина относительного изменения доходности актива I за предыдущий период;

• y _t _ 1,j - величина относительного изменения доходности актива ; за предыдущий период.

Рассмотрим ортогональную модель обобщенной авторегрессионной условной гетеро-скедастичности (OGARCH). В ней предлагается трансформировать матрицу доходностей в набор портфелей с ключевой характеристикой, предполагающей некоррелированность, что позволяет прогнозировать волатильность каждого портфеля в отдельности.

В первую очередь необходимо трансформировать матрицу доходностей по формуле (2).

и = L ху ,

где   и - матрица некоррелированных портфелей;

• L - матрица размерности К х К , состоящая из собственных векторов корреляционной матрицы рассматриваемых К активов;

у - матрица доходностей рассматриваемых К активов.

Еще одним подходом к построению ковариационной матрицы представляется модель постоянных условных корреляций (DСС), где ковариационная матрица рассчитывается по формуле (3).

Z t = D_t R D_t ,

где   Z_t — ковариационно-вариационная матрица;

R - матрица выборочной корреляции между стандартизированными остатками;

D_t - матрица условной волатильности.

Матрица выборочной корреляции R_t моделируется по формуле (5), где Q_t в свою очередь определяется уравнением (4).

R t = (diag⁽Q t ) 2 Q t (diag⁽Q t )) ^1/2 ,

где R_t - матрица условных корреляций, Q_t - симметричная, положительно определенная матрица (5).

^Q t = (1 ^- а ^{- p)Q} * + az t-i z ’-i + P^Q t—i

Q* = i/TZLiZtzt, где   Q* - безусловная ковариационная матрица стандартизированных остатков (формула (6));

а и р - параметры, такие, что а,р > 0 и а + р <  1 для обеспечения свойств положительной определенности и стационарности;

z_t = e_t/a_t - стандартизированные остатки в момент времени t .

Модель реализованной волатильности (Realized Quadratic Covariation, RCov, формула (7)) предложена Т. Андерсеном и соавторами в 2003 г. [8].

^RCoV t = Т^П.г't.t ,

где r_tl - вектор внутридневных значений доходности.

Фактически мы говорим о характеристике финансового разнообразия рассматриваемых активов, входящих в отраслевые индексы или общерыночный индекс. Пусть мы наблюдаем динамику волатильности рыночного индекса, если последняя будет снижаться. Здесь возможны следующие предпосылки: могла снизиться волатильность активов, входящих в рассматриваемый индекс, либо, например, величина попарной корреляции между рассматриваемыми активами.

Таким образом, сформулировано понятие диверсификационного потенциала заданного множества активов как фактора, значимо влияющего на волатильность доходности акций, фондовых индексов, финансовых портфелей, имеющего определяющее значение в механизме трансформации кластеризации волатильности доходности отдельных активов в кластеризацию волатильности доходности на макроуровне и отражающего степень разнообразия их инвестиционных характеристик в восприятии инвесторов. Разработаны инструменты для расчета и моделирования индекса диверсификационного потенциала рынка.

Предлагаем рассчитывать индекс диверсификационного потенциала рынка по формуле (8), где динамика коэффициента корреляции между рассматриваемыми активами рассчитывается на основе моделей динамической корреляции, например семейство DCC или RCov [9].

DI t

^Zi.>j Cor(a_t,a j)._t

п

где   DIt - индекс диверсификационного потенциала рассматриваемого множества активов в момент t;

cor^a^a^ - коэффициент корреляции между активами а , и а , в момент t ;

и - количество пар активов в заданном множестве.

В работе Ф. Корси, опубликованной в 2004 г., предложен метод прогнозирования реализованной волатильности HAR-RV [10]. В основе модели HAR-RV лежит формула (9). На базе данной модели также можно моделировать реализованную корреляцию.

а™_а = c + Р ^(d)RV_t^(d) + Р ^(w) RV_t^(w) + Р (^ RV_t^(m) + е_£+1 ,                    (9)

где ст^^ - оценка предсказания волатильности на один день; RV_t^(d) - оценка реализованной волатильности, w = 5, m = 22, RV_t⁽ⁿ⁾ = (RV_t +-----+ RV_t-Tl+1)/n. , s_t+1 - ошибка модели, подчиняющаяся закону «белого шума».

В таблице 1 приведена информация о финансовых активах, на основе которых будут рассчитываться индексы диверсификационного потенциала соответствующих фондовых индексов (данные от 29.12.2017).

ПАО	Обозначение	Индекс	Объем котировок (день)	Объем котировок (5 мин)
Банк ВТБ	VTBR	MICEXFNL	1 004	105 272
Сбербанк	SBER	MICEXFNL	1 004	105 294
Московская биржа	MOEX	MICEXFNL	1 004	104 989
АФК «Система»	AFKS	MICEXFNL	1 004	103 056
НОВАТЭК	NVTK	MICEXO&G	1 004	104 499
ЛУКОЙЛ	LKOH	MICEXO&G	1 004	105 281
Роснефть	ROSN	MICEXO&G	1 004	105 260
Газпром	GAZP	MICEXO&G	1 004	105 290
ФСК ЕЭС	FEES	MICEXPWR	1 004	104 746
Интер РАО	IRAO	MICEXPWR	986	100 482
ФГК РусГидро	HYDR	MICEXPWR	1 004	105 204
«Российские сети»	RSTI	MICEXPWR	1 004	103 388
«Норильский никель»	GMKN	MICEXM&M	1 004	105 277
Алроса	ALRS	MICEXM&M	1 004	103 567
НЛМК	NLMK	MICEXM&M	1 004	104 838
Северсталь	CHMF	MICEXM&M	1 004	105 028

Индекс диверсификационного потенциала индекса Московской биржи будет рассчитан на основе 13 активов, приведенных в таблице 1. Ввиду того что не во всех отраслях экономики, представленных на фондовом рынке РФ, можно выделить достаточное количество активов с необходимым уровнем внутридневных котировок, мы рассмотрим лишь 4 отрасли и соответствующих им рыночных индекса, а также индекс Московской биржи. АФК «Система» на момент рассмотрения не входила в состав активов, на основе которых рассчитывался индекс MICEXFNL, однако ее рассмотрение оправдано тем, что она входила в состав соответствующего индекса на протяжении практически всего исследуемого периода и являлась достаточно ликвидным активом.

Расчет и моделирование индексов диверсификационного потенциала будем осуществлять на основе семейства моделей Rcov, MEWMA, OGARCH, DCC, ARIMA.

В таблице 3 приведена статистика ежедневных значений индекса диверсификационного потенциала Московской биржи (DPI_MICEX) за период с января 2014 г. по декабрь 2017 г., рассчитанных на основе формулы (7), где для расчета и моделирования ежедневных попарных коэффициентов корреляции использовались модели Rcov, MEWMA, OGARCH, DCC, ARIMA и др.

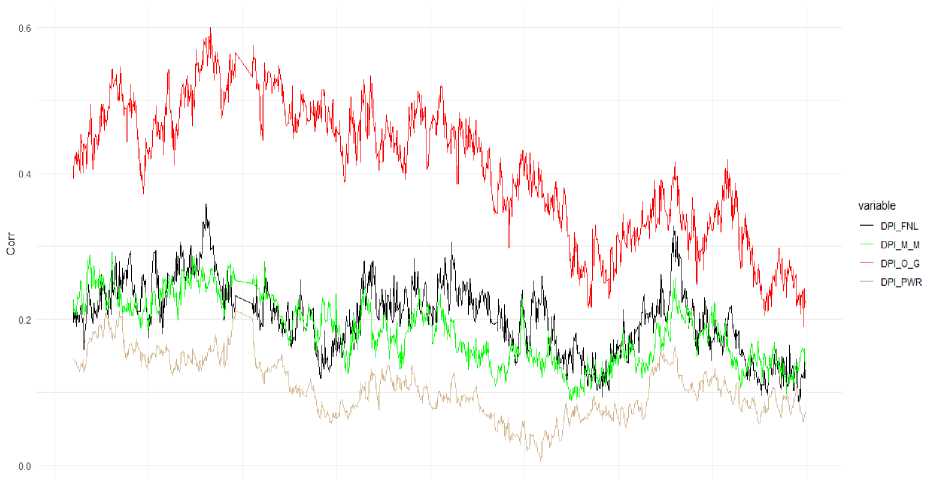
01-ЯНВ-14                                01-ЯНВ-15                                01-ЯНВ-16                                01-ЯНВ-17                                01-ЯНВ-18

Date, День

Актив	N	MIN	MAX	MEAN	MED	SD	SKEWNESS	KURTOSIS
DI_FNL	964	0.03	0.82	0.31	0.30	0.14	0.83	0.97
DI_O&G	964	0.22	0.90	0.53	0.53	0.14	–0.01	–0.88
DI_PWR	964	0.02	0.94	0.39	0.39	0.17	0.23	–0.12
DI_M&M	964	0.00	0.78	0.30	0.28	0.12	0.38	0.46

Таблица 3 – Описательная статистика ежедневных значений индекса диверсификационного потенциала DPI_MICEX за период с января 2014 г. по декабрь 2017 г., рассчитанная и смоделированная на основе различных моделей

Актив	N	MIN	MAX	MEAN	MED	SD	SKEWNESS	KURTOSIS
DPI_MICEX (MEWMAcor)	964	0.05	0.81	0.27	0.24	0.14	1.17	1.40
DPI_MICEX (OGARCHcor)	964	0.19	0.34	0.25	0.24	0.03	0.86	0.72
DPI_MICEX (DCCcor)	964	0.27	0.44	0.29	0.29	0.02	3.43	16.29
DPI_MICEX (Rcov)	964	0.03	0.82	0.23	0.22	0.11	0.88	1.38
DPI_MICEX (HAR-RCov)	964	0.09	0.44	0.23	0.22	0.08	0.26	–0.90
DPI_MICEX (HAR-RCovlog)	964	0.08	0.42	0.22	0.21	0.08	0.25	–0.92
DPI_MICEX (HAR-RCovsqrt)	964	0.08	0.43	0.22	0.22	0.08	0.25	–0.91
DPI_MICEX (AARIMAcor)	964	0.08	0.44	0.23	0.23	0.08	0.22	–0.95
DPI_MICEX (ARIMAcor)	964	0.09	0.46	0.23	0.22	0.08	0.24	–0.95

На рисунке 2 приведена динамика ежедневных значений индекса диверсификационного потенциала DPI_MICEX за период с января 2014 г. по декабрь 2017 г., рассчитанных на основе формулы (8), где для расчета и моделирования ежедневных попарных коэффициентов корреляции использовались модели Rcov, DCC, ARIMA и др.

В таблице 4 приведен сравнительный анализ показателей R ² , Adj.R ² , RSS, MSE, RSE, AIC BIC для моделей MEWMA, OGARCH, DCC, HAR-RC, HAR-RClog, HAR-RCsqrt, ARIMA (1, 1, 1) и AARIMA (auto.arima in r), которые были применены для описания динамики индекса диверсификационного потенциала DPI_MICEX за рассматриваемый период с января 2014 г. по декабрь 2017 г.

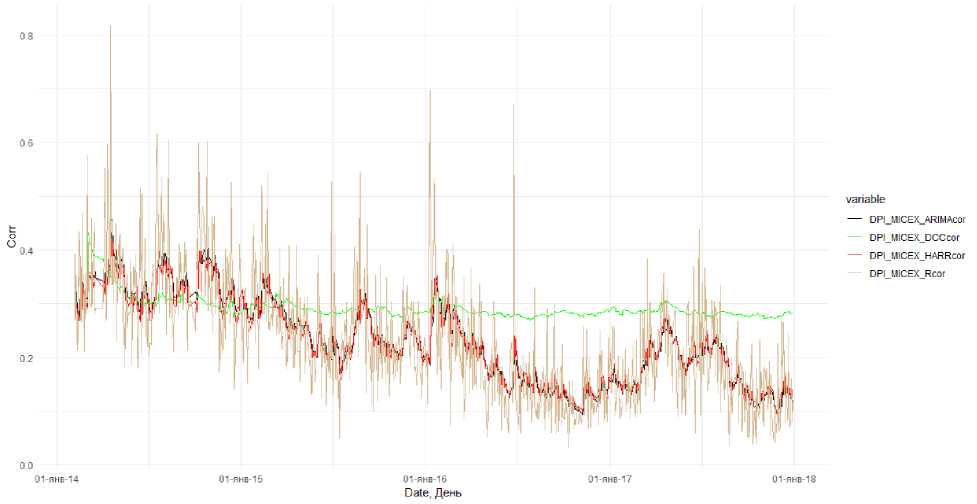
01-янв-16

Date, День variable

— DPI_MICEX_ARIMAcor — DPI_MICEX_DCCcor — DPI_MICEX_HARRcor

DPI_MICEX_Rcor

Рисунок 2 – Динамика ежедневных значений индекса диверсификационного потенциала DPI_MICEX за период с января 2014 г. по декабрь 2017 г., рассчитанная и смоделированная на основе различных моделей

Таблица 4 – Сравнительный анализ показателей R ² , Adj.R ² , RSS, MSE, RSE, AIC BIC исследуемых моделей, описывающих динамику индекса диверсификационного потенциала DPI_MICEX за рассматриваемый период с января 2014 г. по декабрь 2017 г.

Модель	R 2	Adj.R2	RSS	MSE	RSE	AIC	BIC
MEWMA	0.4048	0.4036	12.8592	0.0133	0.0134	–1419.9	–1405.3
OGARCH	0.0201	0.0181	11.8601	0.0123	0.0123	–1497.9	–1483.3
DCC	0.2499	0.2483	13.7535	0.0143	0.0143	–1355.1	–1340.5
HAR-RC	0.4793	0.4777	6.1105	0.0063	0.0064	–2133.2	–2108.8
HAR-RClog	0.4800	0.4783	6.2618	0.0065	0.0065	–2109.6	–2085.2
HAR-RCsqrt	0.4799	0.4783	6.1435	0.0064	0.0064	–2128.0	–2103.6
AARIMA	0.4798	0.4787	6.1248	0.0064	0.0064	–2130.3	–2115.6
ARIMA (1, 1, 1)	0.4916	0.4863	5.9788	0.0062	0.0063	–2137.1	–2083.6

Согласно значениям статистических критериев, демонстрируемым в таблице 4, семейства моделей ARIMA и HAR-RC имеют преимущества при моделировании динамики индекса диверсификационного потенциала DPI_MICEX. Указанные модели имеют минимальные величины AIC и BIC – соответственно –2137.1 и –2083.6 у модели ARIMA (1, 1, 1). Для проверки верности результата для остальных рассматриваемых в работе индексов рассчитаем для них величины соответствующих статистических критериев.

В таблице 5 приведен сравнительный анализ показателей R ² , Adj.R ² , RSS, MSE, RSE, AIC BIC для моделей MEWMA, OGARCH, DCC, HAR-RC, HAR-RClog, HAR-RCsqrt, ARIMA (1, 1, 1) и ARIMA (auto.arima in r), которые были применены для описания динамики индексов диверсификационного потенциала отраслей MICEX_FNL, MICEX O&G, MICEX_PWR и MICEX_M&M и DPI_MICEX за рассматриваемый период с января 2014 г. по декабрь 2017 г.

В таблице 5 приведены результаты регрессионного анализа по сравнению подходов к моделированию динамики индекса диверсификационного потенциала (формула (8)), произведенного на основе расчета динамики попарных коэффициентов корреляции доходности соответствующих акций на основе модели Rcov (формула (7)), с подходами соответствующего расчета на основе моделей MEWMA (формула (1)), OGARCH (формула (2)) и DCC (формула (3)). Согласно данным таблицы 5, если сравнивать по критерию Adj.R ² , то подходы на основе модели AARIMA (auto.arima in r) являются предпочтительными в 3 случаях из 5, а подход на основе ARIMA (1, 1, 1) – в 2 из 5. Если же судить по критерию AIC, то подход на основе HAR-RC выигрывает по этому критерию в 2 случаях из 5, на основе модели AARIMA (auto.arima in r) – в 2 случаях из 5, а на основе ARIMA (1, 1, 1) – в 1 случае из 5. Остальные статистические критерии также свидетельствуют о преимуществе моделей семейства ARIMA и HAR-RC. Базой для сравнения служили значения DPI, рассчитанные на основе Rcov [11].

Таблица 5 – Сравнительный анализ показателей R ² , Adj.R ² , RSS, MSE, RSE, AIC BIC исследуемых моделей, описывающих динамику индексов диверсификационного потенциала отраслей MICEX_FNL, MICEX O&G, MICEX_PWR и MICEX_M&M и DPI_MICEX за рассматриваемый период с января 2014 г. по декабрь 2017 г.

Модель	R2	Adj.R2	RSS	MSE	RSE	AIC	BIC
MEWMA	0	0	0	0	0	0	0
OGARCH	0	0	0	0	0	0	0
DCC	0	0	0	0	0	0	0
HAR-RC	0	0	2	2	2	2	0
HAR-RClog	0	0	0	0	0	0	0
HAR-RCsqrt	0	0	0	0	0	0	0
AARIMA	4	3	3	3	2	2	1
ARIMA (1, 1, 1)	1	2	0	0	1	1	4

Как и при работе с коэффициентами корреляции между отдельными активами, при работе с индексами диверсификационного потенциала предлагается применение смоделированных данных, потому что коэффициенты корреляции, полученные с помощью подхода Rcov, могут содержать большое количество шумов, что может помешать при моделировании волатильности. Согласно полученным результатам, если выбирать между моделями MEWMA, OGARCH, DCC, HAR-RC при моделировании индексов диверсификационного потенциала, стоит отдать предпочтение модели HAR-RC. Однако сама модель HAR-RC в рассмотренной модификации уступает моделям класса ARIMA, в частности ARIMA (auto.arima in r) или, например, ARIMA (1, 1, 1). Но, в отличие от случая моделирования динамики попарных коэффициентов корреляции между отдельными активами, при моделировании динамики индексов диверсификационного потенциала разница между результатами семейства моделей HAR-RC и AARIMA практически отсутствует.

Принцип диверсификации является основополагающим при работе с финансовыми данными. Диверсификация позволяет снижать риски финансовых портфелей при их формировании из отдельных финансовых активов, и сама возможность диверсификации зависит от того, какова корреляция доходностей между этими активами. Однако настоящее исследование продемонстрировало, что, ввиду возможности изменения динамики попарной корреляции между различными финансовыми активами, характеристики возможности осуществлять диверсификацию могут также изменяться во времени. Речь идет как о необходимости пересматривать составы уже сформированных финансовых портфелей, так и о возможности диверсификации в общем случае без учета инструментов осуществления продаж без покрытия. Чем больше финансовые активы ведут себя одинаково, тем меньше возможности для осуществления диверсификации с учетом предложенных ограничений. В предельных состояниях либо все активы ведут себя совершенно по-разному, что означает, что попарные коэффициенты корреляции между ними равны нулю, и тогда возможности для диверсификации максимальны, либо все активы ведут себя совершенно одинаково, что означает равенство попарных коэффициентов корреляции между ними единице, что практически полностью нивелирует возможность осуществлять диверсификацию при заданных ограничениях.

В свою очередь, поведение финансовых активов, а именно динамика их цен формируется под влиянием торговых операций инвесторов. Если инвесторы серьезно обеспокоены определенными макроэкономическими рисками, то их оценка различных финансовых активов на основе одних и тех же мотивов будет приводить к тому, что эти финансовые активы будут ввести себя одинаково, и наоборот: когда инвесторы начинают обращать большее внимание на специфические инвестиционные характеристики финансовых активов, попарные корреляции между ними будут сокращаться. Таким образом, будут ли активы вести себя одинаково или нет, во многом определяется относительной важностью общих макроэкономических условий функционирования на рынке в целом или в конкретном секторе по сравнению с частными инвестиционными параметрами отдельно рассматриваемых активов, что в свою очередь и характеризует динамика диверсификационного потенциала рынка.

На основе предложенных подходов к расчету и моделированию индексов диверсификационного потенциала – как отраслевых, так и рынка в целом – можно более точно анализировать текущее состояние рынка в каждый отдельный момент, а именно определять относительную важность общих макроэкономических условий функционирования на рынке в целом или в конкретном секторе по сравнению с частными инвестиционными параметрами отдельно рассматриваемых активов. Предлагается учитывать динамику диверсификационного потенциала рынка при прогнозировании волатильности активов, фондовых индексов, финансовых портфелей, в том числе эффективных по Марковицу. Также отметим важность учета динамики индекса диверсификационного потенциала рынка финансовыми регуляторами, ведь если этот фактор одновременно влияет на во- латильность всех акций, возможно, именно эта переменная может быть индикатором, сигнализирующим о трансформации кластеризации волатильности с уровня отдельных акций на макроуровень [12]. Также считаем возможным применение данного фактора в других макроэкономических моделях в качестве прокси-переменной, отражающей отношение инвесторов к финансовым активам. Чем выше индекс, тем более важны для инвесторов макроэкономические риски по сравнению с непосредственными инвестиционными характеристиками самих активов.

Ссылки:

Vol. 71, no. 2. P. 579–625.