Моделирование криптосистемы с управляемыми

В статье рассмотрен способ повышения криптостойкости аддитивного метода шифрования – метода гаммирования. Суть заключается в том, что при шифровании открытого текста используются различные логические, арифметические и математические операции. При этом синхронно с изменением гаммы предлагается изменять вид выполняемой шифрующей операции. Проведено моделирование данной криптосистемы с помощью программы компьютерного моделирования Multisim. Также предложен переход от операндов целочисленного вида к вещественным числам, что увеличивает число возможных математических операций шифрования и исключены операции, которые нецелесообразно использовать при шифровании.

Постановка задачи

Существует большое число методов шифрования простых в реализации и обладающих высокой криптостойкостью. Среди них можно выделить широко используемый симметричный метод шифрования – метод гаммирования (иногда его называют аддитивным методом). Основная идея шифрования заключается в замене символов открытого текста на числа и суммировании их с псевдослучайными числами, которые называются «гаммой». При этом состав гаммы известен только доверенным лицам на передающей и приемной сторонах.

Известны методы взлома этого шифра [2-3]. Скомпрометировать шифр можно в случаях нештатного использования гаммы (некачественный состав гаммы, малая длина или повторное использование одной и той же гаммы для шифрования разных сообщений).

Еще одним уязвимым элементом в аддитивном шифре является логическая операция ИСКЛЮЧАЮЩЕЕ ИЛИ, которая используется для зашифрования. Другие названия этой операции: неравнозначность, суммирование по модулю два без переносов.

Известно интересное свойство этой логической операции:

M © G © G = M . (1)

Соотношение (1) говорит о том, что наличие четного числа одинаковых слагаемых, участвующих в операции ИСКЛЮЧАЮЩЕЕ ИЛИ, уничтожает эти слагаемые. Таким образом, если опре- делить период гаммы и произвести логическую операцию ИСКЛЮЧАЮЩЕЕ ИЛИ над символами криптограммы с одинаковыми значениями гаммы (с одинаковыми фазами), то можно уничтожить гамму. В результате такого преобразования получаются данные, представляющие собой результат выполнения логической операции ИСКЛЮЧАЮЩЕЕ ИЛИ над символами открытого текста:

R = C i © C + T = M i © G i © , © M i + т © G i + т = M i © M i + т.

Это объясняется тем, что G i = G _{i + T} , то есть элементы гаммы повторяются с периодом Т и поэтому они одинаковые. Если гамма дважды использована для шифрования двух разных текстов, то задача криптоанализа становится еще проще: достаточно выполнить операцию ИСКЛЮЧАЮЩЕЕ ИЛИ над двумя криптограммами. Известен пример неверного использования метода гамми-рования в операционной системе W indows 95. Одна и та же гамма применялась несколько раз для шифрования данных в файлах PWL [6].

Величину R (2) можно назвать разностью открытых текстов (сообщений). Разность R может быть подвержена успешному криптоанализу путем учета статистических закономерностей открытых текстов или использования известных из других источников их особенностей.

Таким образом, в аддитивном методе шифрования из-за симметричности (обратимости) логической операции ИСКЛЮЧАЮЩЕЕ ИЛИ и нештатного использования гаммы существует возможность произвести криптоанализ и восстановить открытый текст даже без знания гаммы. По этой причине представляет интерес исследование шифра, у которого нет подобного недостатка.

Разработка криптосистемы с управляемыми операциями шифрования

Повысить криптостойкость аддитивного шифра можно за счет использования управляемых операций шифрования [1]. Основная идея рассматриваемой криптосистемы состоит в использовании в течение одного сеанса связи не одной, а нескольких различных шифрующих операций.

В этой криптосистеме с изменением значения гаммы варьируются операции преобразования, выполняемые над открытым текстом (на передаче) и над криптограммой (на приеме). Причем на передаче и приеме операции зашифрования и расшифрования должны чередоваться синхронно. Например, если на передаче осуществляется арифметическое сложение символа открытого текста с элементом гаммы, то на приеме нужно вычесть гамму из полученной криптограммы. Синхронизация выполняемых операций должна осуществляться под управлением гаммы, которая одновременно определяет и вид выполняемой операции и участвует в этих операциях.

На рис. 1 показана структурная схема криптографической системы с управляемыми операциями шифрования. Моделирование этой системы было осуществлено с помощью программы Electronics Workbench Multisim 8.2.12 Pro.

Имитация передающей и приемной сторон криптосистемы осуществлялась с помощью двух арифметикологических устройств 74281J. Четырехбитный открытый текст M подавался на вход А первого арифметикологического устройства (АЛУ). Четырехбитная гамма G подавалась на входы В каждого АЛУ. Вид выполняемой операции на передающей стороне задавался с помощью преобразователя кода ПК1. Управляющие сигналы S на приемной стороне формировались с помощью преобразователя кода ПК2. Сигналы с выходов преобразователей кодов подавались на управляющие шины АЛУ. Именно эти сигналы определяли вид выполняемых АЛУ операций. Криптограмма K формировалась на выходе F первого АЛУ. Расшифрование криптограммы осуществлялось на приемной стороне с помощью второго АЛУ. Выполняемые операции синхронно изменялись под управлением гаммы. Принятый открытый текст M' появлялся на выходе F второго АЛУ

Канал связи

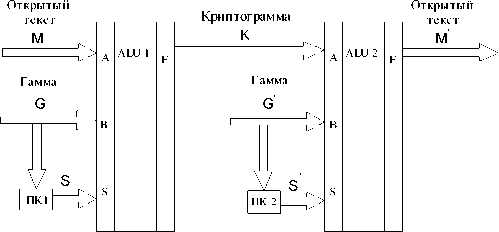
Передающая сторона

Приемная сторона

Рис. 1. Структурная схема криптосистемы

В качестве шифрующих преобразований можно использовать различные логические и арифметические операции, а так же математические функции и их комбинации. Некоторые из них перечислены в таблице 1.

В таблице 1 приняты обозначения: M – открытый текст (сообщение); G - гамма; K - криптограмма; ⊕ – логическая операция ИСКЛЮЧАЮЩЕЕ ИЛИ (неравнозначность); ∞ - логическая операция равнозначность; «+» — арифметическая операция сложение; «–» – арифметическая операция вычитание; черта над переменными обозначает операцию инверсии.

Первые 1 1 операций предполагают работу с целыми числами. Остальные операции предназначены для работы с вещественными числами.

Задачей преобразователей кодов ПК1 и ПК2 являлось синхронное изменение управляющих сигналов. Естественно, что конструкции преобразователей кодов ПК1 и ПК2 были разные, так как при одинаковых входных воздействиях (гамма G) преобразователи кодов должны формировать разные выходные (управляющие) сигналы S и S`.

Преобразователи кодов можно синтезировать различными способами [4-5]: графически (с помощью карт Карно и диаграмм Вейча), аналити-чески(методыКвайна,Мак-Класки,неопределен-ных коэффициентов) и с помощью графических символов, интерпретирующих булевы функции.

Перечисленные способы синтеза (минимизации) трудоемки и имеют ограничения на их использование при числе переменных более 5-6. При разработке рассматриваемой модели криптосистемы преобразователи кодов синтезировались с помощью блока Logic Converter (логический конвертор), который входит в систему моделирования радиоэлектронных устройств Multisim 8.2.12 Pro. Этот инструмент позволяет создавать преобразователи кодов с числом аргументов n ≤ 8 . Для получения математических выражений, описывающих работу ПК, достаточно в конвертор ввести таблицу истинности, которая описывает работу преобразователя кода. Полученные математические выражения затем использовались для построения принципиальной схемы ПК.

Анализ логических и арифметических операций

Рассмотрим подробнее порядок выбора логических и арифметических операций,которые можно использовать для шифрования текста.

Безусловно, при разработке новой криптосисте- мы нужно использовать многократно проверенную

Таблица 1. Операции шифрования

Операции на передающей стороне Операции на приемной стороне 1. Неравнозначность K = M © G Неравнозначность M'= K © G 2. Равнозначность K = M Ф G = M го G Равнозначность M '= K Ф G = K От G 3. Сложение K = M + G Вычитание M'= K — G 4. Вычитание K = M — G Сложение M'= K + G 5. Вычитание K = G — M Вычитание M'= G — K 6. Инверсия от суммы K = M + G Комбинированная разность M'= K — G 7. Инверсия от разности K = M — G Комбинированная сумма M'= K + G 8. Инверсия от разности K = G — M Комбинированная разность M'= G — K 9. Комбинированная сумма K = M + G Комбинированная разность M '= K — G 10. Комбинированная разность K = M — G Комбинированная сумма M'= K + G 11. Умножение K = M • G Деление M = K / G 12. Деление K = M / G Умножение M = K • G 13. Деление K = G / M Деление M = G / K 14. Функциональные K = f (M, G) Функциональные M = f 1 (K, G) 15. Алгебраические K =M n±G s Алгебраические M = n K ∓ G s операцию ИСКЛЮЧАЮЩЕЕ ИЛИ. Кроме того, аналогичными свойствами обладает операция «равнозначность», которая является инверсией от операции ИСКЛЮЧАЮЩЕЕ ИЛИ.

В виду того, что логические операции M от G = M от G эквивалентны операции неравнозначности M ⊕ G ^, использовать все три операции при шифровании не имеет смысла,так как криптограммы дл я них будут од и наковыми. Аналогично операции M ф G = M ф G сводятся к операции равнозначности M ∞ G . Таким образом,из рассмотренных шести операций следует использовать только две:равнозначность и неравнозначность.

Для арифметических операций в дополнительном коде справедливы соотношения:

M - G = G - M = M + G ;

M + G = G - M = M - G ;

G - M = M - G = M + G ;     (3)

G - M = M + G = M - G ;

M - G = g - м .

Использование операций, перечисленных в одной строке, даст одинаковые значения криптограммы при одинаковых значениях гаммы и открытого текста. Из четырнадцати указанных операций целесообразно оставить только пять, например

M + G , M - G , M + G , M - G и G - M .

Помимо изменения шифрующих операций разработанная модель криптосистемы позволила имитировать процедуру смены сеансового ключа. Для этого в модель был введен переключатель А, который изменял таблицу соответствия выполняемых операций и значений гаммы. Другими словами: с помощью этого переключателя одним и тем же значениям гаммы ставились в соответствии иные наборы выполняемых операций.

Одна из множества возможных таблиц истинности, которая описывает работу ПК1 на передающей стороне, представлена ниже. Такие таблицы совместно с гаммой являются ключевой информацией.

Таблица 2. Таблица истинности

№ п/п	Ключ К ( A )	Гамма В 3 В 2 В 1 В 0 ( B C D E )	Операция	Управляющие сигналы S 3 S 2 S 1 S 0	М	cN
0	0	0 0 0 0	M ⊕ G	0 1 1 0	1	X
1	0	0 0 0 1		0 1 1 0
2	0	0 0 1 0		0 1 1 0
3	0	0 0 1 1		0 1 1 0
4	0	0 1 0 0	M ⊕ G	1 0 0 1	1	X
5	0	0 1 0 1		1 0 0 1
6	0	0 1 1 0		1 0 0 1
7	0	0 1 1 1		1 0 0 1
8	0	1 0 0 0	M-G	0 1 1 0	0	0
9	0	1 0 0 1		0 1 1 0
10	0	1 0 1 0		0 1 1 0
11	0	1 0 1 1		0 1 1 0
12	0	1 1 0 0	M+G	1 0 0 1	0	1
13	0	1 1 0 1		1 0 0 1
14	0	1 1 1 0		1 0 0 1
15	0	1 1 1 1		1 0 0 1

В таблице 2 символом «х» обозначены безразличные состояния ПК. Вход Mod определяет, какую операцию выполняет АЛУ: логическую или арифметическую. Входы S ₃ S ₂ S ₁ S ₀ и Mod предназначены для формирования управляющих сигналов, которые позволяют выбрать одну из 32-х возможных операций данного АЛУ.

Для приемной стороны составляется аналогичная по форме таблица истинности.

Внешний вид конвертора, с помощью которого осуществлялся синтез преобразователей кодов, показан на рис. 2.

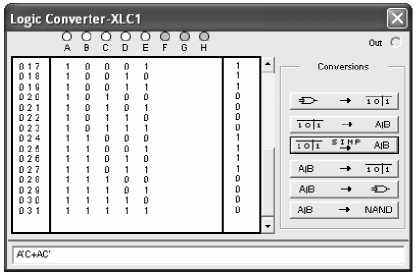
Рис. 2. Логический конвертор XLC1 с изображением фрагмента таблицы истинности (S3)

С помощью логического конвертора и таблицы 3 были получены выражения, описывающие работу ПК1, находящегося на передающей стороне:

S3 = S0 = ΑΒ2 ∨ ΑΒ2

S 2 = S 1 = AB 2 V AB 2 , Mod = b 3    (3)

CN = ΑΒ2 ∨ ΑΒ2 = S3.

Аналогично были получены выражения для ПК2, работающего на приемной стороне.

S3 = S0 = ΑΒ3Β2 ∨ ΑΒ3Β2 ∨ ΑΒ3Β2 ∨ ΑΒ3Β2S2 = S1 = ΑΒ3Β2 ∨ ΑΒ3Β2 ∨ ΑΒ3Β2 ∨ ΑΒ3Β2

Mod = B 3 , C N = AB 2 v AB 2 .

На основании полученных выражений были составлены принципиальные схемы двух преобразователей кодов.Разработанная и исследованная принципиальная схема модели криптографической системы работала с использованием четырех опера-ций:ИСКЛЮЧАЮЩЕЕ ИЛИ,равнозначность, сложение и вычитание.При этом результат вычитания формировался на выходе АЛУ в дополнительном коде.Смена сеансового ключа имитировалась с помощью переключателя А.Схема модели криптосистемы приведена ниже на рис. 3.

Исходный текст, принятый текст,гамма и криптограмма отображались с помощью индикаторов U3…U6. Значения гаммы и передаваемый текст формировались с помощью генератора слов XWG1 (Word Generator).

Преобразователи кодов ПК1 и ПК2расположены в нижней части рис.3.

Как и всякая имитация,разработанная модель не полностью соответствует реальной криптографической системе. Например,при моделировании прини-малось,что соединение между передающей и приемной сторонами происходит по четырем проводам. В реальной криптосистеме связь должна осуществляться по двухпроводной линии.

Кроме того,при моделировании считалось,что операнды,циркулирующие в криптосистеме,явля-ются четырехразрядными целыми числами. Диапазоны изменения чисел составляли 0 ≤ M ≤ 15 и 0 ≤ G ≤ 15 . В действующей криптосистеме разрядность операндов должна быть,по крайней мере,в два раза больше.Кроме того,в реальной криптосистеме при формировании криптограммы возможно использование не только целых,но и вещественных чисел.

В разработанной модели было использовано только четыре шифрующие операции:ИСКЛЮЧА-ЮЩЕЕ ИЛИ,равнозначность,арифметическое сложение и вычитание.Имитация смены ключей осуществлялась только для двух таблиц соответствия значений гаммы и выполняемых операций.

Несмотря на введенные упрощения, модель криптосистемы с управляемыми операциями шифрования позволила проверить работоспособность системы,выбрать виды логических и арифметических операций,имитировать смену сеансового ключа, наметить пути совершенствования криптосистемы.

Выводы

• 1 .В рассмотренной криптосистеме гамма представляет собой равновероятную смесь натуральных чисел, а управляющие сигналы формируются под управлением гаммы.По этой причине каждая из выполняемых операций шифрования становится

• 2 . Переход от операндов целочисленного вида к вещественным числам увеличивает число возможных математических операций шифрования,вклю-чая элементарные испециальные функции. При этом большинство операций не обладают свойством сим-метрии,и гамму нельзя уничтожить при совместной обработке двух криптограмм (даже зашифрованных с помощью одной гаммы).

• 3 .Разрядность гаммы определяет максимально возможное число различных видов операций,ис-пользуемых при зашифровании открытого текста. При использовании восьмиразрядной гаммы можно применить до 256 различных логических,арифмети-ческих,математических операций и их комбинаций.

также равновероятной. Это существенно усложняет работу криптоаналитиков.