Моделирование кристаллизации с учетом двухфазной области

Сложность процессов, протекающих в затвердевающей отливке, побуждает исследователей идти по пути решения определенных частных проблем. Наиболее последовательным подходом в данной ситуации является разбиение всей задачи на масштабные [1] или системные уровни [7]. На каждом масштабном уровне осуществляется построение модели процесса затвердевания, которая учитывает основные особенности поведения расплава на данном уровне. Это обстоятельство и определяет круг задач для субмоделей. На макроуровне наибольшее внимание уделяется тепло- и массопереносу. Модели используются для определения границы затвердевания, тепловых потоков, поля скоростей, распределения концентрации компонентов расплава. Данные модели являются основой для многоуровневого моделирования. Основная задача моделирования - предсказание микроструктуры на основе использования моделей микроскопического роста. В качестве входных параметров используются такие данные с макроуровня, как скорость отвода тепла, концентрация компонентов сплава. Масштаб модели - двухфазная область. Модели микроуровня, как правило, рассматривают процесс зародышеобразования и роста твердой фазы. В этих моделях макроскопическими особенностями процесса можно пренебречь. Входными параметрами являются данные с мезоуровня, масштаб которого - длина дендрита.

. При формулировке многоуровневой модели, кроме указания передачи параметров задачи сверху вниз, необходимо предусмотреть обратную связь (возможно, через другие параметры).

Рассматривается макромодель процесса затвердевания, которая является составной частью многоуровневой модели. Суть модели состоит в том, что затвердевающий слиток представляется в виде четырех пространственных зон. Для каждой из этих зон используется соответствующая модель. Рассмотрим литейную форму с отвердевающим расплавом. Изучаемая система - кристаллизующаяся металлическая отливка состоит из следующих основных элементов: жидкого ядра, двухфазной зоны взвешенных кристаллов, двухфазной области закрепленного каркаса и твердой корки. Очевидно, что каждая подсистема должна описываться своими моделями.

Внимание акцентируется на двухфазной области, поскольку именно здесь осуществляется переход металла из жидкого в твердое состояние и сосредоточены все основные процессы, влияющие на формирование микроструктуры материала.

Математическая модель жидкого ядра

Для жидкого ядра используются определяющие соотношения вязкой жидкости. Кроме того, делается предположение о том, что в жидком ядре нет включений твердой фазы.

Представим жидкое ядро затвердевающей отливки в виде многокомпонентной смеси. Рассмотрим основные уравнения механики сплошных гетерогенных сред для такой смеси [6]. При этом будем полагать, что:

• 1)    химических превращений в жидком ядре не происходит;

• 2)    все компоненты смеси имеют одинаковую скорость.

На первом этапе ограничимся записью уравнений для двухкомпонентного сплава.

Пусть V_L - объем, занимаемый г - м компонентом сплава жидкого ядра, тогда полный объем

(1) где N - количество компонентов сплава ( N = 2).

Плотность вещества компонентов смеси в объеме И будем обозначать через р£ , г = 1,2, причем плотность р = р£ = 22р/. .

Скорости компонентов смеси (согласно второму допущению):

V = V_L-V_Lt, / = 1,2.                                     (2)

Рассмотрим уравнения сохранения массы.

• -^ + V(p_L^)=f.(n_£VpJ₊^^                      ₍₃₎

где J,_L ,i = 1,2, / = 1,2 - интенсивность перехода массы между компонентами смеси; D, , / = 1,2 -коэффициент диффузии компонента смеси.

В отсутствии химических реакций J_LL = 0, z = 1,2, j = 1,2 .

Окончательно (3) можно записать в виде

^+v.(plkJ=V.(dl;vpJ/ = i,2.

Уравнения движения запишем в следующем виде:

°JX^L          ^pj +Yp_1l ,z = 1,2,

7 ‘                    '(5)

Р-чЦ = -PLLJ = l,2,y = 1,2,'

где P_;1 - интенсивность обмена импульсом между фазами; /, - массовые силы, отнесенные к жидкой фазе; a_L - тензор напряжений в жидкой фазе. Из массовых сил будем рассматривать только силу тяжести, то есть f_L=g.

Так как скорости компонентов смеси равны и отсутствуют химические реакции, то P_L,_Lj = 0,i = V2J = V2.

Считается, что поведение жидких металлов (расплавы металлов) достаточно хорошо может быть описано в приближении вязкой жидкости. При этом возможны различного рода усложнения выбранной модели - нелинейная вязкость, сжимаемость и т.д. Запишем определяющие соотношения вязкой жидкости в следующем виде'

5г =-P8⁺K^l.№ + ^VxD,

)                                                        (6)

[P = PV,APlJ, где р = р^Т.р.р,J - материальная функция; D - тензор скоростей деформаций.

В случае связанной постановки эта система дополняется уравнением теплопереноса, что позволяет учитывать взаимное влияние процессов теплопроводности и массопереноса [9]:

(дТ               _{( х}                                (7)

+ VZ..V7J=V.(XV7'),                           V где c = c^7',pL ) - теплоемкость; Х = Дт,р1 J - коэффициент теплопроводности.

Таким образом, система уравнений для жидкого ядра состоит из соотношений (4), (5), (6), (7).

Математическая модель двухфазной области

Рассмотрим уравнения механики сплошных гетерогенных сред для твердой и жидкой фаз затвердевающего слитка. Основные допущения принимаем аналогично сформулированным в [8]:

• 1.    Среда является многоскоростной.

• 2.    Давление создается только несущей средой - расплавом.

• 3.    Частицы твердой фазы представляются в виде шарообразных частиц одного размера, которые не взаимодействуют между собой и стенками литейной формы.

• 4.    Взаимодействие частиц твердой фазы с расплавом обусловлено наличием вязких сил.

Представим рассматриваемую область в виде 4-компонентой смеси (два компонента в двух фазах), каждая из которых занимает свой объем. В этом случае полный объем

=                                                             (8)

где P_s , / = 1,2 - твердая фаза г - го компонента; V_L, i = 1,2 - жидкая фаза / - го компонента.

Объем, занимаемый твердой и жидкой фазами, можно определить следующими соотношениями:

(9) v-v_sw_L.

Для каждого из компонентов можно определить плотность его вещества в объеме V - p_Si, p_s^, p_Li и р^ соответственно, причем плотность смеси Р = Ps, + Рц ~Ру + 0^ •

Аналогично (9) определим плотности твердой и жидкой фаз:

Рз = Рх, ⁺ Ps₂ >

(Ю)

' Рд = Ра + Ра -

Р = Ps ⁺ Pl-

Пусть компоненты смеси, относящиеся к одной фазе, имеют одинаковую скорость:

^=К,^1Д(11)

Рассмотрим уравнения сохранения массы:

V        VLDS Vp, +Л„ т J, „,

О Z           \ Di r 01 /       0^0]'

Ot

-^+у-Ь, r )= v_P, uj_L, -j_s, +j_sl,

--MV p C ~V./) Vp I+/_$S ~^LS ^^I S ’

+ f (p_r k)=v (d, Vp, )+Л, +     + J_SL ,

^S₂S_V^— ~^-SA ^A⁵! " ^—'^SJ₁ ’Jl^ — SyL₂ ’

J ~ ""^AA ^S₂L_V ~ ~^1^_г ^L,S, ~ ~^ S₂L₂ 1

где J_?q , p = L,S,q = L,S,i = 1,2,/ = 1,2- интенсивность перехода массы между компонентами смеси, D_Pt, р = L,S, к = 1,2 -коэффициент диффузии компонента смеси.

Очевидно, что из определения компонентов смеси, некоторые коэффициенты массоперехода являются нулевыми, так как компоненты литейного сплава не могут претерпевать взаимные химические превращения в процессе литья и затвердевания Таким образом, остается определить две материальные функции, отвечающие за обмен массой между компонентами смеси во время фазового перехода:

? =ЛЙ- ,рл 1

• -уЗ!       ТцО] \ ’ 0’ L 7 Г- р^ р

J.s =J_Ls (ту.у.р Лр = ьул = \,1.                      ⁽¹³>

Скорость диффузии в твердой фазе существенно меньше скорости диффузии в жидкой фазе, поэтому диффузным членом в уравнении для твердой фазы можно пренебречь.

Окончательно (12) можно записать в виде

^Л.(р^) = ^,

- V • (p_L/J = V • \p_Li Vp_LtJ_LA ,p = L, S,k = 1,2.

Уравнения движения запишем для твердой и жидкой фаз.

+ V ■ ^y_sV_s) = V ■ + p_sf. + P_LS,

ApyyiW^ ^pLfL +PSL..

CT

1r где Ра - интенсивность обмена импульсом между фазами; fs - массовые силы, отнесенные к твердой фазе; JL - массовые силы, отнесенные к жидкой фазе, 9S -тензор напряжений в твердой фазе, 6 L - тензор напряжений в жидкой фазе.

Из массовых сил будем рассматривать только силу тяжести, то есть f_s=f_L-g

Пусть P_SL можно представить в виде суммы слагаемых;

Pgr ⁼             + AL-S     •                                      (16)

где R_SI - сила межфазного взаимодействия из-за сил трения,, сцепления и т.д; ^l-a ⁺ la Ум " обмен импульсом за счет фазового перехода; К_м - скорость твердой фазы на границе с жидкой фазой.

Принимая гипотезу о полном прилипании расплава и включений твердой фазы, получаем

V^-V.^V.,                              (17)

Из соотношений (15.3) и (17) следует, что

Rls—Rsl                                 (18)

В работах [3] и [5] предлагается следующая зависимость для R_LS (при этом полагается, что включения твердой фазы не взаимодействуют друг с другом и занимают пренебрежимо малый объем):

где А = ^Цу$-УД; CD - коэффициент сопротивления; г - характерный размер 4psr включений твердой фазы.

Окончательно имеем ps — = V • д5 + ps/s + A(VS - yL),

™ = v-5l+PtA +*

Процесс кристаллизации протекает с выделением тепла, в связи чем требуется дополнить уравнение теплопроводности (7) источниковым членом:

pcf—+ KL(21)

^ = И^^Г.РрД р = L,S, к = 1,2   - мощность внутренних источников тепла, учитывающих выделение тепла при фазовом переходе из жидкого состояния в твердое

Для определения мощности источника W₄ при кристаллизации наиболее часто используют следующее соотношение ([4], [9]):

где О - удельная теплота фазового перехода, т| - объемная доля твердой фазы

Учитывая, что объемная и массовая концентрации могу, быть выражены друг относительно друга, модифицируем соотношение, заменив долю твердой фазы на плотность твердой фазы:

иуРе^.                         ,23)

Полная система уравнений для двухфазной области состоит из соотношений (13), (14), (20); неизвестные величины -р_А, Т, У_р, 8_р. Наибольшие трудности вызывает определение коэффициентов J_LSk, ответственных за фазовый переход. Именно эти коэффициенты отражают перенос массы между фазами (компонентами гетерогенной смеси).

Определение коэффициентов интенсивности межфазного массопереноса

Задача определения интенсивности перехода массы между компонентами смеси в соотношении (14) может быть решена двумя способами:

• 1)    прямым моделированием на более мелком масштабном уровне;

• 2)    использованием макросоотношений.

Первый вариант предполагает не только более точное описание процесса кристаллизации, но и большую универсальность подхода, в то время как использование макропараметров ограничено наличием опытов для сплавов с конкретным химическим составом в конкретном технологическом процессе.

Идея использования мезоуровня для получения необходимых данных о ходе процесса кристаллизации состоит в следующем. В модель мезоуровня закладываются соотношения, позволяющие описать рост и зарождение кристаллов в расплаве при определенных параметрах окружающей среды. В дальнейшем в качестве параметров среды выступают данные с макроуровня, что позволяет осуществить прямое моделирование процесса кристаллизации в одной макроточке. Результатом моделирования является либо функция для определения количественного значения межфазных коэффициентов, либо сами эти значения. В качестве входных параметров моделирования на мезоуровне можно предложить следующие.

• 1)    скорость компонентов смеси,

• 2)    плотность компонентов смеси,

• 3)    температуру,

• 4)    напряжения в расплаве и твердой фазе.

В настоящее время большое распространение получил подход, основанный на построении зависимости прироста твердой фазы от переохлаждения как температурного, так и концентрационного. Это означает, что наиболее значимыми параметрами являются температура и химический состав (плотность компонентов смеси), а остальные параметры могут вносить лишь небольшие корректирующие поправки.

Материальные функции, отвечающие за фазовый переход в (13), можно представить в следующем виде

=.r_LtP_Sk,k-U,                                (24)

где J£ - интенсивность фазового массоперехода из твердой фазы в жидкую.

Так как наиболее существенным параметром, влияющим на фазовый переход, является температура (точнее, переохлаждения), то построим функцию интенсивности фазового перехода как степенную функцию переохлаждения:

>К_к⁼ ~^^а^ "Т^ Д = 1,2,                            (25)

где а, - калибровочные параметры, определяемые из опыта.

Сравнение с опытными данными

Для процесса кристаллизации согласно [10] характерны приведенные на графиках временные зависимости для локального изменения интенсивности фазового массоперехода в некоторой экспериментальной точке (рис. 1) и изменения количества твердой и жидкой фаз (рис. 2 и 3, соответственно). Для всех графиков по оси абцисс отложено относительное безразмерное время от начала процесса фазового перехода, по оси ординат отложены соответствующие безразмерные величины (интенсивность, плотности). Эти данные были получены при экспериментах со алюминиевыми сплавами.

Рис. 1. Локальное изменение интенсивности фазового массоперехода

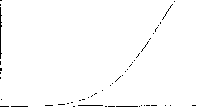
Рис. 2. Рост количества твердой фазы

Рис.З. Уменьшение количества жидкой фазы

Моделирование на основании соотношений (14), (21), (24) и (25) позволяет получить следующие результаты для различных режимов охлаждения. Под режимом охлаждения будем понимать скорость отвода тепла. Очевидно, что такая скорость неоднородна по сечению отливки и изменяется (уменьшается) по мере удаления от стенки литейной формы. Скорость отвода тепла оказывает существенное влияние на процесс кристаллизации, а именно, на интенсивность образования новой фазы. Таким образом можно выделить две противоположные ситуации: для пристеночных областей характерны большие градиенты температур, а в центре отливки наблюдается медленное охлаждение Для большей части отливки реализуется что-то среднее. Скорость отводы тепла очень тесно связана с темпом кристаллизации [9].

На рисунках показаны кривые охлаждения (рис. 4), интенсивности фазового перехода (рис. 5) и изменение количества жидкой фазы (рис. 6) для трех случаев отвода тепла: 1 - быстрого, 2 - обычного, 3 - медленного.

Рис.4. Изменение температуры

В случае быстрого отвода тепла большой градиент температуры приводит к тому, что тепло, выделяемое в ходе процесса кристаллизации, практически полностью отводится. Это приводит к некоторому изменению кривой охлаждения (изменение угла наклона) При медленных скоростях охлаждения наблюдается обратная ситуация; интенсивность фазового перехода мала, и поэтому в ходе процесса кристаллизации выделяется мало тепла и характер кривой охлаждения также меняется мало.

Рис. 5. Изменение интенсивности фазового перехода

Качественно иная ситуация наблюдается в средних областях отливки. Градиент температур достаточен, чтобы обеспечить высокую интенсивность фазового перехода. Это в свою очередь приводит к большому' выделению теплоты кристаллизации и наблюдается локальное повышение температуры. С уменьшением количества жидкой фазы температура снова начинает падать.

■■■^•■■■Л»*"------------ —..........  - -

Рис. 6. Изменение количества жидкой фазы

В целом, полученные результаты в достаточной степени соответствуют модельным представлениям. Однако наблюдается некоторая нестабильность для режимов среднего охлаждения. Необходимо дальнейшее исследование с целью расширения круга параметров при конструировании зависимости для JJ . Предполагается использовать какие-либо монотонно возрастающие параметры процесса, например, физическое время.

Выводы

• 1.    Сформулирована математическая постановка задачи кристаллизации металлического сплава как задача механики гетерогенных сред.

• 2.    Определен вид коэффициента межфазного массопереноса.

• 3.    Численным моделированием получены результаты, согласующиеся с модельными представлениями о ходе процесса кристаллизации.

• 4.    Показано, что зависимость коэффициента межфазного массопереноса только от температуры (переохлаждения) не является достаточной. Намечены пути дальнейшего исследования.

Работа выполнена при поддержке гранта Министерства образования РФ по фундаментальным проблемам металлургии № 98-26-5.2-33.