Моделирование критических явлений в обобщенной модели Ван дер Поля

1 ПРЕДВАРИТЕЛЬНЫЕ СВЕДЕНИЯ

В рамках настоящей работы будет рассматриваться класс трехтемповых быстро-медленных автономных динамических систем, зависящих от одного дополнительного скалярного параметра р:

ей = f (x,y,z,e,p), y = g(x,y,z,e,p),              (1)

z = e h(x,y,z,e,p), где под точкой подразумевается дифференцирование по времени t, параметр 0 < ε << 1 обуславливает малое возмущение системы, а х, у и z — быстрая, медленная и сверхмедленная переменные соответственно.

Напомним, что траектория сингулярно возмущенной системы называется траекторией-уткой, если она вначале проходит вдоль притягивающего листа медленного инвариантного многообразия, а затем — вдоль его отталкивающего листа, причем пройденные расстояния в обоих случаях сравнимы с единицей [1, с. 110]. Само понятие траектории-утки (фр. canard) было впервые использовано французскими математиками в работах [2,3].

Использование траекторий-уток получило весьма широкое распространение при моделировании критических явлений различной природы [1,4, 18,19].

Естественным обобщением траекторий-уток, которые по сути являются одномерными инвариантными многообразиями, являются их многомерные аналоги — инвариантные многообразия со сменой устойчивости [5-7], эпизодически возникающие в случае нетривиальной размерности медленной переменной. Подобно траекториям- уткам, такие многообразия располагаются одно- Балабаев Михаил Олегович, аспирант кафедры дифференциальных уравнений и теории управления.

временно как вблизи притягивающего, так и вблизи отталкивающего листов медленного инвариантного многообразия [1, с. 280].

Особым классом подобных многообразий следует считать уточные поверхности, которые характеризуются тем, что через каждую их точку проходит траектория-утка. Фактически, такие поверхности целиком состоят из траекторий-уток, каждая из которых моделирует критическое, но при этом безопасное протекание некоторого процесса. Подобный подход к моделированию критических явлений был впервые применен в работе [8], а затем многократно использован в работах [9-11].

Пусть ^ : R 4 ^ R - достаточно гладкая функция, задаваемая равенством

V ( x,y,z,e ) =

fgh

II f gh f gh

Говорят, что ϕ определяет кривизну фазового потока исходной динамической системы в соответствующей точке.

Как хорошо известно [12,13], функция ϕ является глобальным инвариантом, то есть имеет место тождество dv = 0:

||dx + dydy + ^dz + ^de = 0 .

Это равенство лежит в основе метода кривизны потока. Используя его, можно получить систему алгебраических уравнений [14,15], решения которой позволяют параметризовать инвариантное многообразие с некоторой точностью.

Предположим, что скалярный параметр р допустимо использовать в качестве управляющего воздействия для исходной модели (1). Подобрав надлежащим образом функцию р = р(х, у, z, ε), можно достичь того, что разрыв инвариантного многообразия вдоль кривой срыва будет устранен одновременно во всех точках. Таким образом, в некоторых случаях удается склеить притягивающий и отталкивающий листы инвариантного многообразия вдоль всей кривой срыва, получив тем самым инвариантное многообразие со сменой устойчивости.

Подобный подход в контексте метода кривизны потока был впервые применен в работах [9-11] для нахождения инвариантных поверхностей со сменой устойчивости в модели трехмерного автокаталитического реактора, самосопряженной модели ФитцХью-Нагумо и модели Копера.

• 2.    ОБОБЩЕННАЯ МОДЕЛЬ ВАН ДЕР ПОЛЯ

Важность осциллятора Ван дер Поля для прикладных задач сложно переоценить. Он нашел свое применение в моделировании множества физических, биологических, геологических и сейсмологических процессов.

В настоящей статье мы будем рассматривать один из частных случаев обобщенной модели Ван дер Поля, первоначально упомянутый в работе [16] и затем частично исследованный в работе [17]:

ex = px2 + qx3 — y, y = x - z, (2) z = e (^ — ry).

В этой упрощенной модели ^ является бифуркационным параметром, скалярные величины p > 0, q < 0 и r > 0 полагаются действительными порядка О (1) при б ^ 0, а малое возмущение определяется вещественнозначным параметром 0 <  б << 1. В рамках данной работы мы ограничимся рассмотрением области R + = { ( x,y,z ) | x,y,z Е R , x,y,z> 0 } , интересной с физической точки зрения.

Очевидно, что медленное многообразие модели (2) является цилиндрической поверхностью, образующей для которой служит кубическая парабола y = px2 + qx3.

Кривая срыва модели (2) является совокупностью двух прямых и, очевидно [1, с. 19], определяется из системы fpx2 + qx3 — y = 0,

У 2 px + 3 qx ² = 0 .

Для нас представляет интерес только одна из этих прямых, имеющая непустое пересечение с областью R + и определяемая вектор-функцией

J 2 p 4 p ³ 1

1 - 3 q, 27 q 2 ’ Т

Для инвариантного многообразия системы (2) мы будем использовать параметрическое представление, которое удобно искать в виде разложения по степеням малого параметра:

• У = У ^{( x,z,e} ) = У o ^{( x,z ) +} У 1 ^{( x,z} ) e. (3)

Воспользуемся методом кривизны потока [14, с. 192]. В соответствии с ним первые два коэффициента разложения будут иметь вид:

У о( x,z )= px ² + qx ³ ,             (4)

z-x

У 1 ^{( x}, ^z ) = 4----—2 *             (5)

4 px +6 qx ²

Как видим (см. рисунок 1), полученное инвариантное многообразие системы претерпевает разрыв вдоль кривой срыва за исключением единственной точки, соответствующей z = 1. Траектория-утка, соответствующая данным рисунка и полученная в работе [17], ожидаемо проходит именно через эту точку.

Воспользуемся подходом, изложенным в работе [15], чтобы устранить разрыв вдоль всей кривой срыва. Для этого вместо параметра р исходной системы подставим функцию

3 qz p ⁽ z ) = —2"" .

Это позволит устранить разрыв в функции (5), причем вышеуказанная подстановка оставляет в силе налагаемое моделью (2) ограничение р >  0, если только мы находимся в интересующей нас области R ³ ₊ .

Подставив функцию p(z) в коэффициенты (4) и (5), мы можем выписать первое приближение (3) инвариантного многообразия, не имеющее разрыва вдоль кривой срыва (см. рисунок 2). Таким образом, можно говорить о том, что найденная функция (6) является нулевым приближением склеивающей.

Более того, если для исходной модели (2) зафиксировать некоторую точку на кривой срыва и вычислить уточное значение, то соответствующая величина p(z) будет близка к этому значению. Это означает, что полученное инвариантное многообразие не просто имеет смену устойчивости вдоль кривой срыва, но и целиком состоит из траекторий-уток, то есть принадлежит к классу уточных поверхностей.

• 3.    ВЫВОДЫ

Для частного случая обобщенной модели Ван дер Поля при помощи метода кривизны потока была получена склеивающая функция

p ( z,e ) = — ³ qz + O ( e ) .

Она позволила склеить притягивающий и отталкивающий листы интегрального многообразия вдоль всей линии срыва и тем самым построить инвариантное многообразие со сменой устойчивости:

У ( x, z, e ) = qx ³ — ³ qx-z — -1- e + O ( e ² ) .

• 2     6 qx

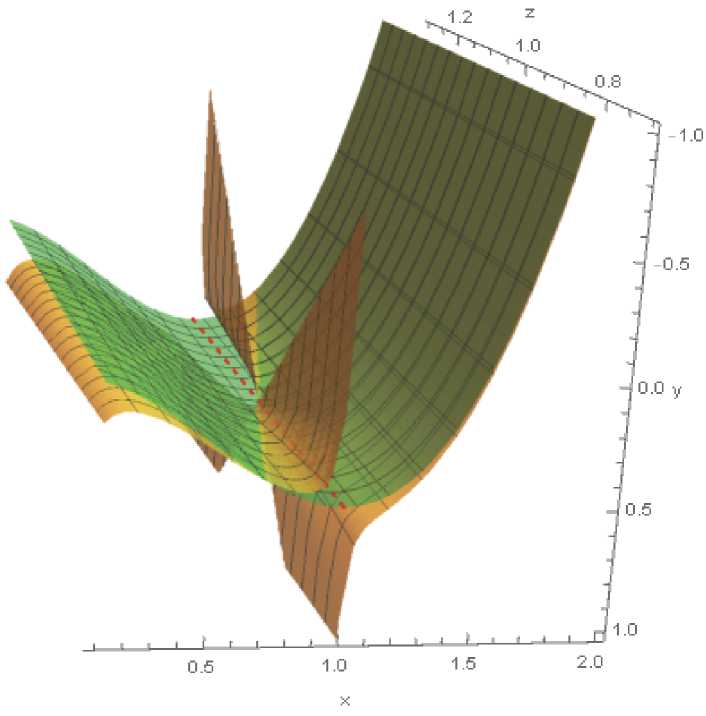
Рис. 1. Медленная поверхность (зеленая), инвариантное многообразие (желтое) и кривая срыва, ε = 0.141, р = 1.5, q = –1, r= 0.2, µ = 0.036

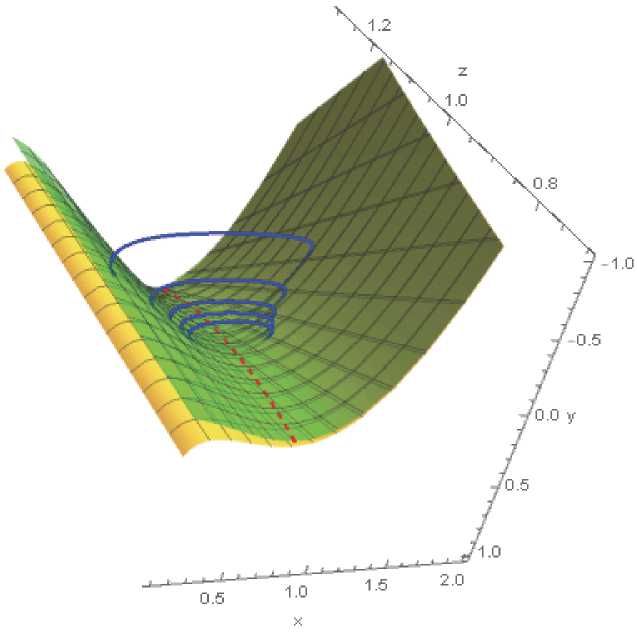
Рис. 2. Медленная поверхность (зеленая), инвариантное многообразие со сменой устойчивости (желтое) и траектория, ε = 0.141, q = –1, r = 0.2, µ = 0.036, начальные условия X ₀ = 0.33, у₀ = 1.035, Z ₀ = 0.204342