Моделирование кривых намагничивания ансамблей наночастиц с комбинированной симметрией магнитной анизотропии

Термины «нанонаука», «нанотехнология», «наноструктурированные» (материалы и объекты) сегодня уже прочно вошли в повседневную жизнь, ими обозначают приоритетные направления научно-технической политики в развитых странах [1]. Так, в США действует программа «Национальная нанотехнологическая инициатива», Евросоюз недавно принял шестую рамочную программу развития науки, в которой нанотехнологии занимают главенствующие позиции. Минпромнауки РФ и РАН также имеют перечни приоритетных, прорывных технологий с приставкой «нано». По оценкам специалистов в области стратегического планирования, сложившаяся сейчас ситуация во многом аналогична той, что предшествовала тотальной компьютерной революции, однако последствия нанотехнологической революции будут еще обширнее и глубже.

Рис . 1.

Направление векторов

В настоящее время внимание большого числа исследователей наноматериалов обращено к магнитным наночастицам. Такие частицы в магнитном отношении делятся на два класса: суперпарамагнитные (обычно с размерами 1–10 нм) и ферромагнитные (10–50 нм). Последний класс представляет наибольший интерес для практических применений наночастиц [2]. Ему и посвящена эта работа. Ферромагнитные наночастицы с размерами 10–50 нм находятся в однодоменном состоянии. Ансамбли таких наночастиц, как правило, образуют систе- напряженности магнитного поля и локальной намагниченности

мы со случайно ориентированной магнитной анизотропией. Описание кривых намагничивания ансамблей наночастиц строится на основе классической модели Стонера – Вольфарта (СВ) [3; 4]. Теоретические кривые намагничивания, полученные в модели СВ для частиц с одноосной и кубической анизотропией, хорошо известны исследователям. При интерпретации экспериментальных кривых намагничивания ансамблей наночастиц с трехосной кристаллографической магнитной анизотропией (ОЦК Fe, ГЦК Co и Ni и т. д.) реализуется более сложная ситуация. Так, например, наночастицы никеля обладают ГЦК кристаллической решеткой и характеризуются кубической магнитной анизотропией. В то же время, будучи подвергнуты одноосному растягивающему либо сжимающему напряжению, за счет магнитоупругого эффекта энергия магнитной анизотропии частицы будет иметь и одноосный (магнитоупругий) вклад. К такому же результату приведет и анизотропия формы частицы, индуцирующая соответствующую магнитную анизотропию. В этом случае результирующая симметрия магнитной анизотропии изменяется, что приводит к необходимости обобщения модели СВ [5; 6]. Необходимость такого обобщения проявилась при попытке интерпретировать результаты недавних экспериментов по перемагничиванию одной ферромагнитной наночастицы, полученные с помощью SQID [5; 6]. Такое обобщение предпринималось в работах [7; 8], где было изучено влияние комбинированной магнитной анизотропии на перемагничивание одной частицы (астроиду перемагничивания).

Задача этой работы состояла в изучении кривых намагничивания ансамблей наночастиц, полученных в композиционном варианте модели СВ, когда каждая наночастица одновременно подвержена влиянию кубической кристаллографической магнитной анизотропии и случайно ориентированной одноосной магнитной анизотропии, связанной, например, со случайной ориентацией анизотропных по форме частиц.

Метод и модель

В нашей модели рассматривается ансамбль невзаимодействующих монодо-менных частиц, имеющих кубическую анизотропию. Распределение ориентаций легких осей намагничивания (ЛОН) случайно для каждой частицы. Если для конкретной частицы с кубической анизотропией выбрать направление осей системы координат вдоль ЛОН (рис. 1), то направление локальной намагниченности частицы m и напряженности внешнего магнитного поля H можно описать углами ( J , j ) и ( J ₀ , j ₀ ) либо направляющими косинусами ( a ₁ , a ₂ , a ₃ ) и ( b ₁ , b ₂, b ₃ ). При одноосной анизотропии вдоль ЛОН направляем ось Oz .

Полная энергия частицы для случая одноосной магнитной анизотропии будет иметь вид [3; 4]:

E u □ K u a 2 m s H a 1 b 1 a 2 b 2 a 3 b 3 ,                       (1)

а для случая кубической магнитной анизотропии:

E _c □ K i a 2 a 2 a 2 a 2 a ² a 2 m _s H a 1 b 1 a 2 b 2 a 3 b 3 ,         (2)

где m s – намагниченность насыщения одной частицы; H – внешнее магнитное поле; K u и K 1 – константы одноосной и кубической магнитной анизотропии частицы; a1 , a2 , a3 – направляющие косинусы орта локальной намагниченности u                                                                        u m ; b1 , b2 , b3 – направляющие косинусы вектора внешнего магнитного поля H .

Расчет кривых намагничивания в данной работе осуществлялся следующим образом. Из полностью размагниченного состояния (случайное направление u u вектора m и H U 0) с малым шагом dH начинаем изменять внешнее магнитное поле. Для каждого нового значения поля методом градиентного спуска [9] определяем направление вектора локальной намагниченности, соответствующее минимуму энергии частицы. Поиск нового устойчивого направления m каждый раз проводился из предыдущего равновесного состояния. Движение намагниченности частицы при таком подходе оказывается необратимым, что и приводит к возникновению магнитного гистерезиса. Кривые намагничивания ансамбля случайно ориентированных частиц в классической модели СВ получаются усреднением равновесных кривых намагничивания индивидуальных частиц.

Полученные с использованием энергии системы в форме (1) и (2) кривые намагничивания приведены на рис. 2. Намагниченность нормировалась к намагниченности насыщения M _s ансамбля частиц. На вставке к рисунку показаны изоэнергетические поверхности для энергии анизотропии, отображающие ее пространственную симметрию.

В комбинированной модели, рассматриваемой нами, каждая наночастица одновременно подвержена влиянию кубической кристаллографической магнитной анизотропии и случайно ориентированной одноосной магнитной анизотропии. В этом случае полная магнитная энергия одной частицы запишется в виде:

r ' z^ 2     7^     2 2       2 2       2 2

E U K _u a 3 K i a 1 a 2   a 2 a 3 a 3 a ^

m _s H a 1 b i    a 2 b 2    a 3 b 3 .

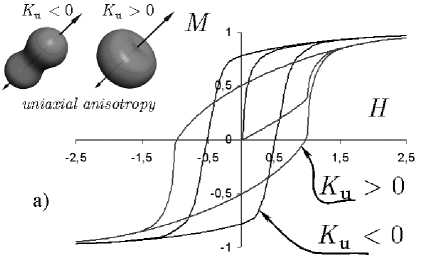
Рис . 2. Кривые намагничивания и изоэнергетические поверхности для: а) одноосной магнитной анизотропии; б) кубической магнитной анизотропии

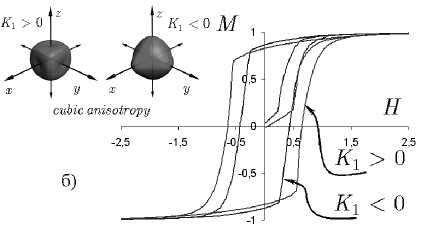
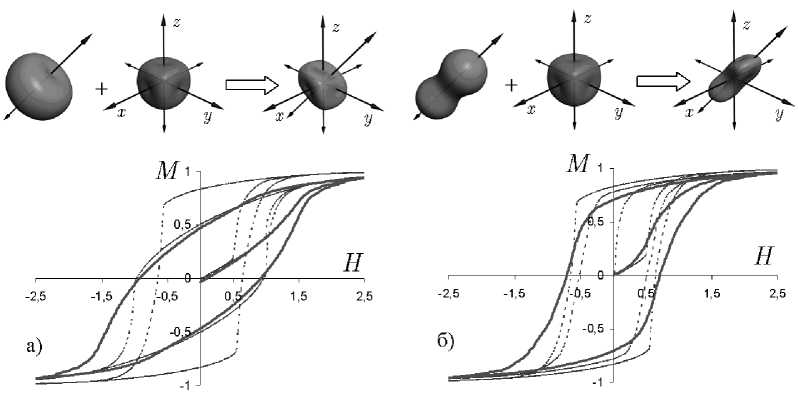
Рис . 3. Изменение вида петель гистерезиса в комбинированной модели поля анизотропии

Примеры кривых намагничивания, полученные с использованием энергии в форме (3), приведены на рис. 3. Изоэнергетические поверхности для энергии анизотропии в этом случае (на вставке к рисунку 3) имеют более сложную симметрию, что в результате и приводит к изменению формы кривой намагничивания.

Результаты и обсуждение

В общем случае энергия кубической и одноосной магнитной анизотропии может быть как положительной, так и отрицательной. Поэтому нами были рассчитаны четыре набора кривых намагничивания, соответствующие промежуточному (композиционному) варианту модели СВ с различными вкладами одноосной и кубической анизотропии: ( K _u □ 0; K 1 □ 0), ( K _u □ 0; K 1 □ 0), ( K _u □ 0 ; K 1 □ 0), ( K _u □ 0; K 1 □ 0). Мы исследовали зависимость магнитных величин от процентного вклада k _u энергии одноосной анизотропии в полную энергию магнитной анизотропии. При k _u □ 0 и 100% мы получаем классические кривые модели СВ, характеризующиеся хорошо известными параметрами. Обсудим параметры кривых намагничивания, полученных в композиционной модели СВ.

На рис. 4 представлена зависимость приведенной остаточной намагниченности от процентного вклада k _u энергии одноосной анизотропии в суммарную энергию магнитной анизотропии. Видно, что в чистых состояниях при k _u □ 0% и k _u □ 100% мы получаем известные ранее из классической модели СВ величины M _r. Переход же между k _u □ 0% и 100% оказался немонотонным. Для K _u □ 0 этот переход характеризуется неизменностью M _r в интервале k _u от 0 до 10–30%, далее следует уменьшение M _r в интервале k _u от 10–30% до 30–40%, при этом M _r уменьшается до величины 0, 7 . В интервале k _u от 30 – 40% до 90% следует плато, после чего при переходе к чистой одноосной анизотропии k _u □ 100% происходит рост M _r до величины 0,8 (соответствующей случаю отрицательной одноосной магнитной анизотропии).

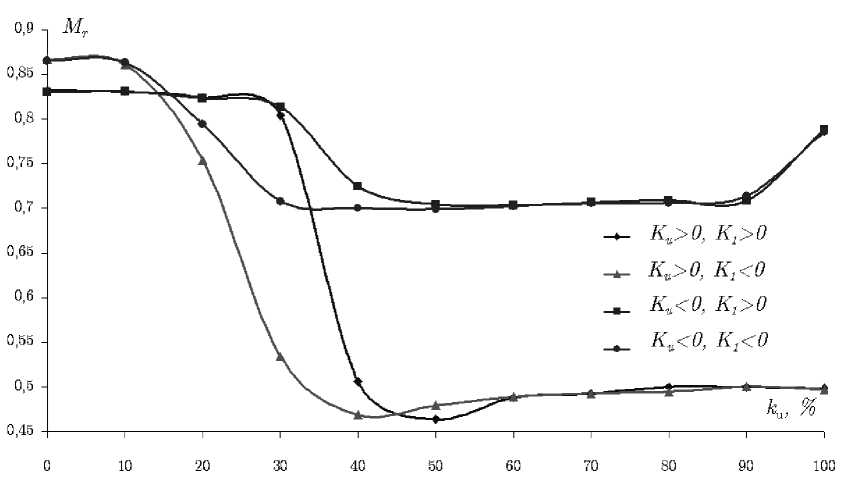
Рис . 4. Зависимость приведенной остаточной намагниченности M _r от вклада в результирующую анизотропию одноосной фазы

Для случая K _u □ 0 остаточная намагниченность M _r при непрерывном переходе от состояния с кубической анизотропией ( k _u □ 0%) к состоянию с одноосной анизотропией ( k _u □ 100%) также изменяется немонотонно. При увеличении вклада одноосности от 0 до 10 – 30% остаточная намагниченность M _r практически не изменяется. Далее происходит ее резкое уменьшение до значения M _r □ 0,46 при 40 и 50 %-м присутствии одноосной фазы. При k _u □ 60% намагниченность M _r приближается к значению 0, 5 и остается такой на интервале k _u от 60 до 100% .

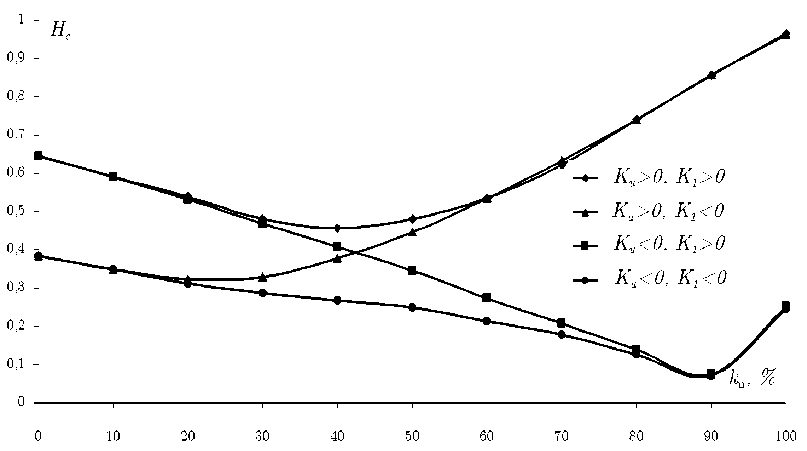
Рис . 5. Зависимость коэрцитивной силы H _c от вклада в результирующую анизотропию одноосной фазы

На рис. 5 представлена зависимость коэрцитивной силы H _c от процентного вклада энергии одноосной анизотропии в суммарную энергию магнитной анизотропии. В процессе перехода от системы с одноосной анизотропией к системе с кубической магнитной анизотропией коэрцитивная сила монотонно убывает до своего минимального значения при некотором значении k _{u min} , а затем происходит ее увеличение на интервале от k _{u min} до 100% . При переходе от системы с отрицательной одноосной к системе с кубической анизотропией k u min □ 90%. При переходе от системы с положительной энергией одноосной анизотропии к системе с кубической магнитной анизотропией k u min ~ 30% □ 40% .

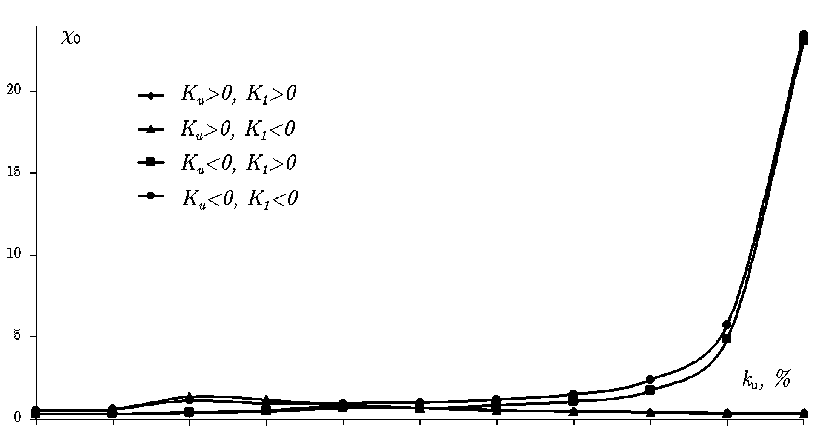
На рис. 6 и 7 представлены зависимости начальной и максимальной воспри-имчивостей для рассматриваемой нами комбинированной модели СВ. Начальная восприимчивость ^{c 0} несколько увеличивается в диапазоне 20–40% и резко возрастает для случая K u □ 0 от 80% до 100% . Максимальная восприимчивость c _max в общих чертах повторяет ход начальной восприимчивости. Отличие здесь проявляется в том, что в чистых состояниях k _u □ 0 и k _u □ 100% максимальная восприимчивость всегда оказывается несколько большей, чем в соседних состояниях со смешанной анизотропией.

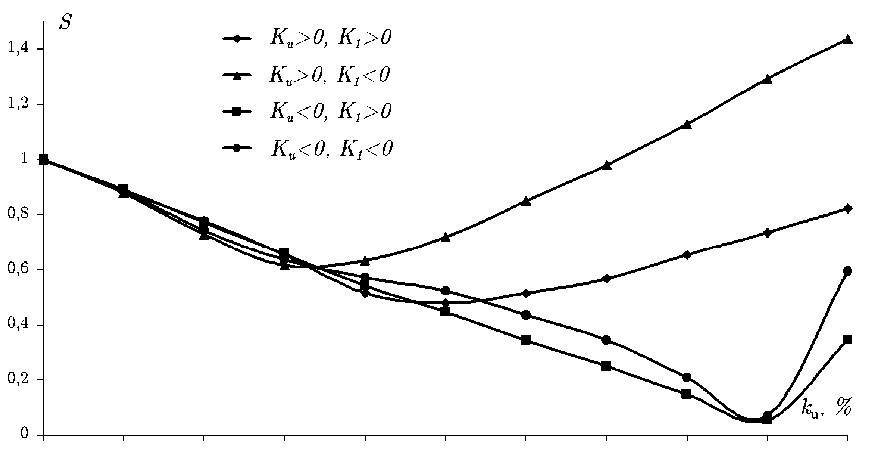
Величины площади петель гистерезиса S (нормированные к площади петли при k _u □ 0% ), отражающие энергетические потери за цикл перемагничивания, приведены на рис. 8. Из этого рисунка видно, что поведение величины S при изменении k _u качественно повторяет зависимость H c k u (рис. 5). Здесь при переходе системы от K _u □ 0 к K 1 □ 0 и от K _u □ 0 к K 1 □ 0 минимальное значение площади наблюдается при k _u □ 90% . При переходе от K _u □ 0 к K 1 □ 0 k _umin □ 30% , а при переходе от K _u □ 0 к K 1 □ 0 k _{u min} □ 50%.

0%     10%     20%     30%     40%     50%     60%     70%     80%     90%     100%

Рис . 6. Зависимость начальной восприимчивости c ₀ магнетика от вклада в результирующую анизотропию одноосной фазы

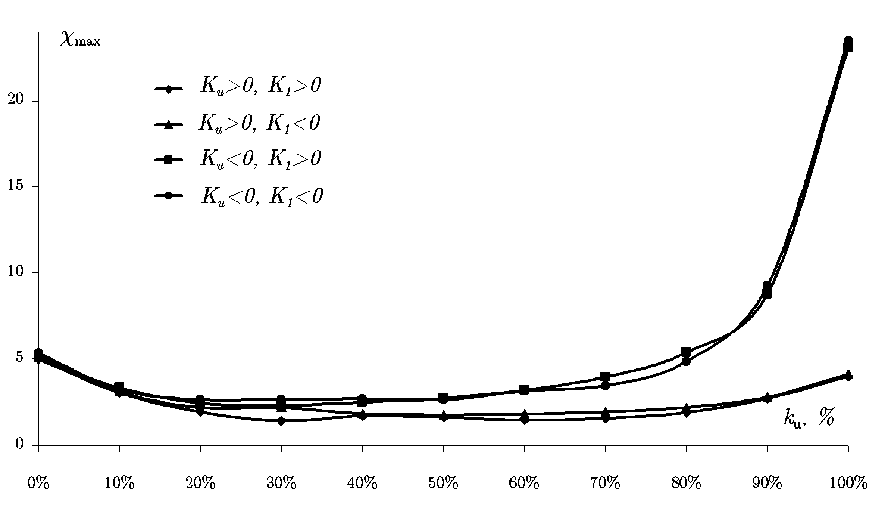
Рис . 7. Зависимость максимальной восприимчивости c _max от вклада в результирующую анизотропию одноосной фазы

0%     10%     20%     30%     40%     50%     60%     70%     80%     90%     100%

Рис . 8. Зависимость площади петли гистерезиса от вклада в результирующую анизотропию одноосной фазы

Обнаруженная немонотонность магнитных свойств при непрерывном переходе от ансамбля наночастиц с кубической анизотропией к ансамблю наночастиц с одноосной анизотропией, с нашей точки зрения, значительно повышает практическую значимость результатов, представленных на рис. 4–8. Дело в том, что ансамбли однодоменных ферромагнитных наночастиц широко применяются на практике в качестве материалов для постоянных магнитов. При этом значительные усилия направляются на оптимизацию таких магнитных свойств, как остаточная намагниченность M _r , коэрцитивная сила H _c и площадь петли гистерезиса S . Неприменимость линейных правил при непрерывном переходе от ансамбля наночастиц с кубической анизотропией к ансамблю наночастиц с одноосной анизотропией означает, что правильно оптимизацию перечисленных параметров можно осуществить лишь на основе результатов, представленных на рис. 4–8.

Отметим, что сравнение полученных в этой работе модельных кривых намагничивания и экспериментальных кривых для наночастиц может быть использовано для получения дополнительной информации об их магнитных константах. Например, в работе [10] авторы обращают внимание на расхождение экспериментальных кривых ансамбля наночастиц с трехосной кристаллической магнитной анизотропией (среда для магнитной записи Maxwell MF2-HD) и теоретических кривых, полученных в модели СВ. Качественно для полей H □ H _c авторы [10] объясняют это расхождение неоднородностью величины поля анизотропии, однако такой подход совершенно не способен объяснить расхождение экспериментальных и теоретических кривых намагничивания в области остаточной намагниченности. В то же время результаты, полученные в нашей работе (см. рис. 4), не только объясняют это расхождение, но и позволяют численно оценить отношение энергии одноосной и кубической анизотропии в этом материале, приготовленном на основе магнитных наночастиц.

В заключение отметим, что новейшие практические приложения магнитных наночастиц на сегодняшний день исключительно обширны: от медицинской диагностики и транспорта лекарств до нанозондов, наноманипуляторов и современных компьютеров. Ферромагнитные наночастицы в предшествующие десятилетия сыграли центральную роль в беспрецедентном росте индустрии записи и хранения информации и, как ожидается, сохранят этот свой статус в ближайшем будущем. Результаты по кривым намагничивания ансамблей наночастиц с комбинированной симметрией магнитной анизотропии, полученные в этой работе, с нашей точки зрения, важны при экспериментальном изучении и разработке новых магнитных материалов на основе наночастиц.