Моделирование ламинарного свободно конвективного течения в длинном вертикальном цилиндре

Хороший обзор литературы по данной тематике представлен в работе Гангули и др [1]. Они же успешно зафиксировали возникновение многоячеистых видов движения, механизм неустойчивости в вертикальной щели с жидкостями различного числа Прандтля. Прогнозирование ячеистых форм для воздуха и кремниевого масла хорошо согласовывалось с экспериментальными данными, опубликованными в литературе. Для жидкостей различного числа Прандтля определена первичная причина формирования ячеек при переходе от ламинарного течения к турбулентному при высоких критических числах Рэлея. Формирование третичных ячеек очень хорошо смоделировано средствами CFD (вычислительной механикой жидкости). Была проанализирована неустойчивая природа ячеек и замечено их квазипериодическое поведение. Установлена степенная зависимость числа Грасгофа от числа Прандтля Pr для диапазона 0.71 7.

Родригес и др. [2] моделировали средствами CFD конвективный теплоперенос в вертикальном цилиндрическом резервуаре с водой. Большое внимание уделено построению сетки. Задача решалась в нестационарной постановке. Было просчитано 42 варианта переходных режимов h для различных удлинений 1,5≤ d ≤3,5 с целью определить зависимость числа Нуссельта от времени (h – высота цилиндра, d — его диаметр).

Решение для задачи течения и теплообмена в круглой вертикальной трубе вдали от входа при граничных условиях второго рода впервые по

лучено Г.А. Остроумовым [3-4]. В его работах рассматривается суперпозиция вынужденной и свободной ламинарной конвекций. Предполагается, что имеет место горизонтальный и вертикальный градиент температур. В приведенном примере (при отсутствии горизонтального градиента температур) поток имеет строгую симметрию. Одним из частных случаев является случай отсутствия вынужденного движения. Также в [4] выведены линеаризованные уравнения гравитационной конвекции, физически соответствующие движению частиц жидкости параллельно образующим вертикального цилиндрического канала. Приведено решение для установившегося конвективного течения в вертикальном канале круглого сечения. Отмечена диаметральная антисимметричность скоростей и температур относительно продольной оси при отсутствии вертикального градиента температур (рис. 1).

В [4] также представлены результаты экспериментальных исследований. Одна из приведенных фотографий конвективного потока воды с добавленной алюминиевой стружкой демонстрирует характер течения в круглом вертикальном цилиндре с неизолированными стенками и нагретым дном. Поскольку стенки неизолированные, то вертикальный градиент температуры будет приблизительно постоянным за счет постоянных потерь тепла. На рис. 2 видно, как осесимметричный поток (по периферии жидкость поднимается, по оси – опускается) самопроизвольно сменяется антисимметричным (справа жидкость поднимается слева – опускается).

Ниже численно решена задача о свободноконвективном движении воды в цилиндре. Диаметр цилиндра принят равным 0,05 м, торцы предполагаем теплоизолированными, на стенках поддерживается температура, изменяющаяся с вертикальной координатой z по формуле

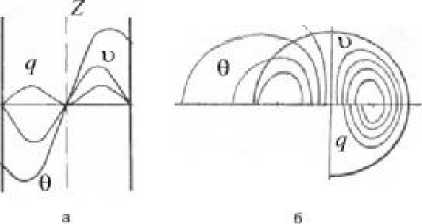
Рис. 1. Распределение скоростей, температур и тепловых потоков [4]:

а – распределение температур θ , скоростей υ и тепловых потоков q по диаметру вертикального канала кругового сечения;

б – изолинии равных температур , скоростей и тепловых потоков по поперечному сечению вертикального канала

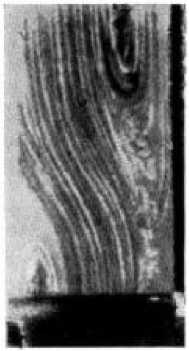
Рис. 2. Тепловая конвекция в трубке круглого сечения [4]

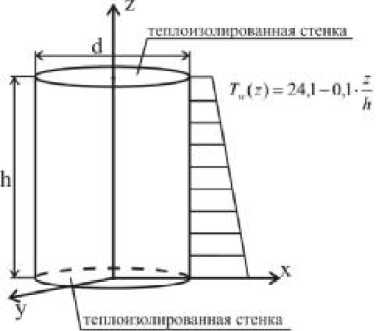
Рис. 3. Координаты и граничные условия

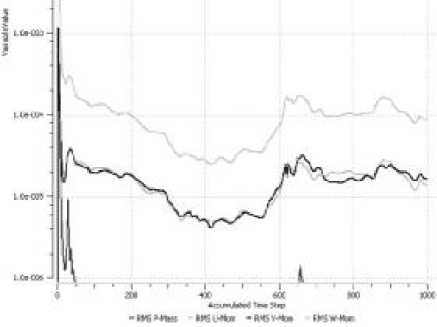
Рис. 4. Среднеквадратические невязки при решении задачи в Ansys CFX

T w (z)= 24,1 - 0,1 ⋅ ^z h

(рис. 3). Для удлинения

ние достигнуто. График изменения невязок представлен на рис. 4.

Было проведено 5 расчетов для цилиндров

h d =30 , рассмотрен перепад температур 0,3, 0,6,

h

различного удлинения ( _d =2, 5, 10, 20, 30). На

0,9 и 1,2.

Решение полных уравнений движения, неразрывности и энергии выполняется методом конечных объемов средствами программного комплекса Ansys CFX.

Используется структурированная гексаэдричес-кая сетка. Количество элементов в поперечном сечении 8000. В продольном направлении количество «сечений» будет зависеть от высоты цилиндра h , и выбирается таким образом, чтобы удлинение каждого элемента сетки было близко к единице. Отметим, что для данной задачи сетка с количеством элементов в 64 раз меньшим (500 элементов в сечении) дает тот же результат при решении.

Поскольку картина движения на 500-ом, на 700-ом и на 1000-ом шаге одинакова, считалось что развитое стационарное конвективное тече- рис. 5 представлены изоповерхности равной вертикальной составляющей вектора скорости для разных удлинений цилиндра. Стрелками указано направление вертикальной составляющей вектора скорости. Из этого же рисунка видно, как меняется характер течения при увеличении удлинения. Явно выделяются области нисходящих и восходящих потоков. Отчетливо видно, что при

h d =20 можно выделить область, в которой имеют место две «струи», по одной из которых вода движется вниз, по другой – вверх, причем они закручены друг относительно друга таким образом, что вращение жидкости вокруг оси происходит против часовой стрелки. Жидкость, двигаясь по одной из «струй», частично переходит

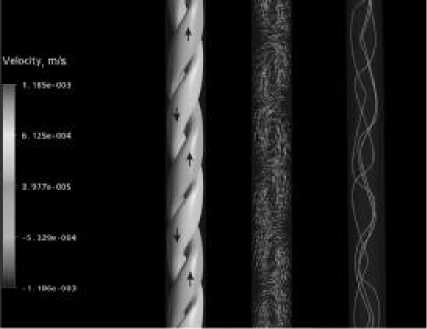
Рис. 6. Изоповерхности равной вертикальной составляющей вектора скорос _r ти (максимальная величина вектора скорости | V | = 0,8 ⋅ 10 ^{- 3} м/с), поле вектора скорости в вертикальном сечении цилиндра, проходящем через ось симметрии, линии тока в средней части

Рис. 5. Изоповерхности равной вертикальной составляющей вектора скорости (изовелы) для разных удлинений цилиндра во встречную, образуя подобие вихрей. Однако, как видно из рис. 6 (линии тока) основная масса жидкости действительно образует «струи».

На рис. 7 представлено поле вектора скорости в поперечном сечении цилиндра. При сравнении рис. 7 и рис. 1 видно, что распределение скорости в поперечном сечении согласуется с приближенным решением, полученным Остроумовым.

Наиболее простая картина течения наблюдается при небольшом удлинении (рис. 8). В двух частях цилиндра – в верхней и нижней образуются как бы вихри, не обладающие строгой осевой симметрией. Движение вверх по средней части в верхней половине разворачивается, идет

h

вертикального цилиндра ( _d =30)

вниз вдоль стенок, затем раздваивается на две

h

широкие струи (рис. 5, d =2), симметричные от- носительно оси z. Затем, сливаясь в нижней половине цилиндра, продолжает движение по центральной части вниз, разворачивается у нижнего основания вверх. Далее картина симметрична описанной.

Полученные при данном моделировании результаты хорошо согласуются с экспериментальными данными. Фотография описанного в [4] эксперимента (рис. 2) показывает картину, похожую на движение около основания цилиндра

(

h

Рис. 7. Поле вектора скорости в поперечном сечении цилиндра в средней его части

Рис. 8. Поле вектора скорости в продольном

h

_d =30, максимальное значение скорости

сечении цилиндра ( _d =2, максимальное

| V ^r | = 1,8 ⋅ 10 ^{- 3} м/с )

значение скорости | V | = 0.8 ⋅ 10 ^{- 4} м/с)

(рис. 5). Действительно, симметричное движение около основания на малом расстоянии от него сменяется антисимметричным, похожим на канатное плетение.

Количественно интенсивность конвективного движения можно оценить, вычислив величину:

Q*=∫ρ⋅wr ⋅dS

S, где ρ – плотность, S – площадь поперечного сечения, w – вертикальная составляющая скорости.

В табл. 1 приводятся значения величины в зависимости от удлинения цилиндра. Видно, что эта величина немного увеличивается с ростом удлинения цилиндра.

В той же таблице представлена величина Δp , равная разности значения гидростатического давления покоящегося столба воды pстат и давления p , полученного при численном решении рассматриваемой задачи (в одной и той же точке на оси симметрии цилиндра), где pстат= p0+ρ0(1+β(T-T0)(h-h0)),

β – коэффициент теплового расширения, T – температура, p ₀ – давление в некоторой базисной точке, высота которой h ₀ , T ₀ – температура, при которой ρ = ρ ₀ . Видно, что увеличивается пропорционально удлинению цилиндра.

Также была проанализирована зависимость Q ^* от перепада температур между концами цилиндра (характер изменения температуры на боковой стенке тот же, что и ранее). Для удлинения 30 были просчитаны 5 случаев (см. табл. 2).

Установлено, что увеличение перепада температур усиливает конвекцию. Также с ростом Δ T увеличивается Δ p .

Величина Δ p изменяется в зависимости от координаты z монотонно, не испытывая каких-либо заметных пульсаций или отклонений от линейного закона.

Проведенное моделирование показало наличие заметного конвективного движения в вертикальном цилиндре. Это движение не обладает осевой симметрией и качественно сходно с данными экспериментов. Количественный анализ показал, что увеличение удлинения цилиндра приводит к росту интенсивности конвективного движения и росту отклонения значения давления около нижнего основания цилиндра от гидростатического давления. Такой же эффект наблюдается и при увеличении перепада температур между основаниями цилиндра. Установлено, что при удлинении, более 20, можно выделить течение в средней части, обладающее свойством антисимметрии. Полученные данные могут быть использованы для сравнения с приближенными методами решения основных уравнений и проверки адекватности предположений, упрощающих решение задачи.