Моделирование механических испытаний образца-сегмента композитного фланца кожуха авиадвигателя

Страумит Илья Сергеевич, инженер кафедры механики композиционных материалов и конструкций Гринев Михаил Анатольевич, заместитель начальника конструкторского отдела состояние, композиционный материал, стекло-жесткость прочностных расчетов с помощью математических моделей [4, 5].

Для подтверждения результатов расчетов проводятся эксперименты на образцах-сегментах, вырезанных из натурных корпусных деталей. Условия испытания образов-сегментов отличаются от условий нагружения корпусных деталей в процессе эксплуатации. Для подтверждения возможности переноса результатов испытаний на натурную деталь необходимо использовать математическую модель образца-сегмента, разработка которой и являлась целью настоящей работы.

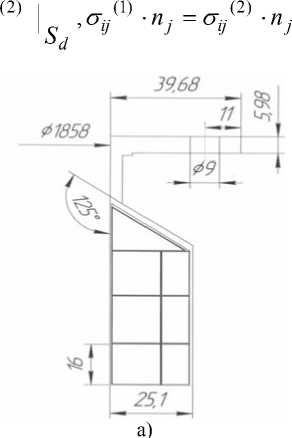
Постановка задачи. Объектом исследования являлся типичный многослойный торцевой фланец композитного кожуха авиационного двигателя (рис.1, а). Фланец изготовлен из стеклопластика на основе ткани с укладкой слоев вдоль образующей и в окружном направлении. Для проведения испытаний из корпусной детали вырезаются образцы-сегменты, включающие участок фланца и кожуха, состоящий из наружных и внутренних силовых слоев и резонансных ячеек треугольного и прямоугольного сечения. В модели учитывается анизотропия и схема укладки слоев, при этом слои, расположенные рядом друг с другом и имеющие одинаковое направление укладки, объединены в один сплошной объем для уменьшения размера конечно-элементной модели. На торцевом участке фланца расположены отверстия диаметром 9 мм под крепежные болты. Для более точного описания экспериментальных условий нагружения в расчетную модель был введен жесткий торцевой элемент, имитирующий участок образца в испытательной оснастке.

Для моделирования нагружения образца при механических испытаниях к нижней части жесткого торцевого элемента прикладывалась равномерно распределенная растягивающая нагрузка. Образец нагружался распределенным давлением 1 КПа по торцу жесткого элемента площадью 2.887∙10^-3 м². Общее усилие нагружение составляет F=2,887 Н. На боковых поверхностях жесткого элемента задавались условия шарнирного опирания, что определяло прямолинейное перемещение нагружающего устройства, имитирующего ход траверсы испытательной машины. Ширина площадки опирания по внутренней поверхности фланца, имитирующей условия крепления в болтовом соединении, задавалась равной δ ш =9 мм, что соответствовало шайбе диаметром Ø ш =18 мм.

Ставится задача определить напряженно-деформированное состояние образца-сегмента при механических испытаниях, провести анализ полей напряжений в слоях образца, оценить его статическую прочность и сравнить с результатами лабораторных испытаний.

Математическая постановка. Математическая постановка пространственной задачи теории упругости для неоднородного анизотропного тела в вариационной формулировке описывается следующей системой уравнений [4, 5]. Вариация функционала Лагранжа при отсутствии массовых сил имеет вид:

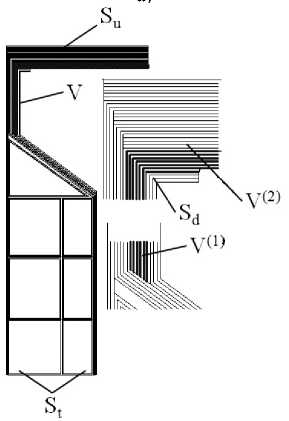
δJu = ∫εijCijklδεkldV -∫pi ⋅δuidS,(1) V st где εij и δεij – тензор и вариация тензора деформаций, Cijkl – тензор упругих модулей, δui – вариация вектора перемещений, рi – вектор внешних сил, действующих на площадке St. Исследуемая конструкция соответствует многосвязной области V, которая имеет внешнюю границу S=Su1+Su2++Su3+St+St0 и состоит из подобластей V(p), соответствующих слоям стеклопластика различной ориентации, с межслойной границей Sd (рис. 1,б). Дополнительными условиями для функционала (1) являются известные геометрические уравнения Коши и кинематические граничные условия на поверхностях Su1, Su2 и Su3, на участке шарнирного опирания:

u_z = 0

S u x = 0 S u 1

S u 2

u

я

=0 I

S u 3

и условия идеального контакта на межслойной границе S d

u_i   = u_i

S^d .(3)

б)

Рис. 1. Геометрическая модель и расчетная схема

На поверхности S t0 внешние силы отсутствуют. Для каждого ортотропного слоя V ^(p) ( p ) компоненты тензора модулей упругости C ijkl зависят от ориентации слоя относительно глобальной системы координат. Компоненты тен- ( p )

зора C_ijkl можно определить в локальной системе координат слоя через технические упругие постоянные по известным соотношениям. Свойства стеклопластика в проведенных расчетах принимались в соответствии с техническим паспортом изделия. Преобразование компонент тензора C _i ⁽ _jk ^p _l ⁾ из локальной системы координат слоя в глобальную систему координат

выполнялось по известным формулам тензорного преобразования. В рассматриваемой конструкции композитного фланца имело место несколько различных вариантов ориентации слоев тканого стеклопластика относительно глобальной системы координат конструкции.

а)

б)

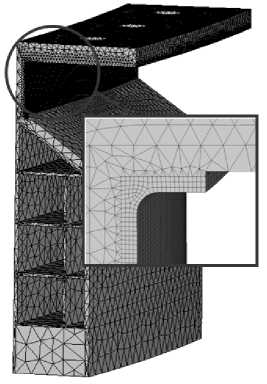
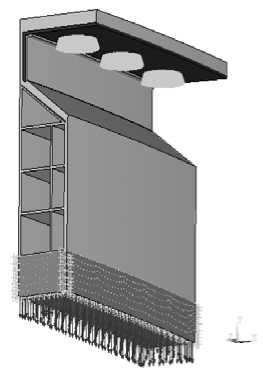
Рис. 2. Конечно-элементная модель (а) и граничные условия (б) для моделирования нагружения образца-сегмента композитного фланца при механических испытаниях

Компьютерная модель. Поставленная задача численно решалась в пакете ANSYS. Дискретизация модели проводилась с использованием пространственных гексаэдрических 20-узловых конечных элементов SOLID95 с нелинейной аппроксимацией функции перемещений [6]. Схема дискретизации образца и граничные условия для моделирования нагружения образца-сегмента при механических испытаниях показаны на рис. 2. Расчеты проводились при единичном значении нагрузки р=1 КПа, равномерно распределенной по поверхности St, что позволило качественно проанализировать распределение напряжений в слоях конструкции и определить наиболее нагруженные зоны. Вследствие линейной зависимости напряжений в слоях конструкции от внешней прикладываемой нагрузки, справедливой для рассматриваемой задачи, сравнение полученных напряжений с пределами прочности материала позволило оценить и критическое значение распределенной нагрузки р, соответствующее потере несущей способности конструкции.

Анализ результатов расчетов. В результате проведенных расчетов получены поля напряжений и деформаций в исследуемом образце. В качестве примера на рис. 3, а показано поле осевых напряжений σ zz (Sy) и деформированное состояние образца при данном нагружении. Анализ полей напряжений показал, что наиболее нагруженной зоной образца-сегмента фланца является участок перегиба армирующих слоев при переходе с цилиндрической на торцевую часть фланца (зона №1) между первым и вторым слоем вблизи зоны перегиба слоев (рис. 3). Этот вывод совпадает с полученными ранее результатами расчетов полноразмерного фланца при эксплуатационных нагрузках, проведенного в осесимметричной постановке [5]. Однако расчеты полноразмерного фланца [5] показывают наличие в конструкции второго нагруженного участка, также в зоне перегиба слоев, при переходе с цилиндрического участка фланца на оболочку кожуха (зона №2 на рис. 3,а.) Данная зона при эксплуатационных нагрузках подвергается значительному изгибу, и в армирующих слоях возникают значительные межслойные напряжения, сопоставимые с напряжениями на торцевом участке. Результаты моделирования механических испытаний образца-сегмента показывают, что при растяжении образца-сегмента второй участок образца (зона №2) сравнительно мало нагружен, межслойные напряжения в данной области в 1,5 раза ниже, чем в наиболее нагруженной зоне №1, рис.3,а. Это связано с тем, что нагружающее устройство испытательной машины обеспечивает, практически, линейное перемещение цилиндрической части образца-сегмента фланца и изгиб рассматриваемого участка отсутствует. При эксплуатационной нагрузке возникает изгибающий момент, который и обеспечивает отличие НДС образца и натурной детали.

Таким образом, качественно нагружение образца-сегмента в лабораторных условиях не полностью моделирует нагружение фланца в реальных условиях эксплуатации. Однако поскольку результаты расчетов полноразмерной конструкции фланца показали, что при эксплуатационной нагрузке межслойные напряжения в зоне №1 и в зоне №2 отличаются незначительно (не более 7%), приближенная оценка прочности конструкции фланца может быть получена по результатам испытаний образцов-сегментов.

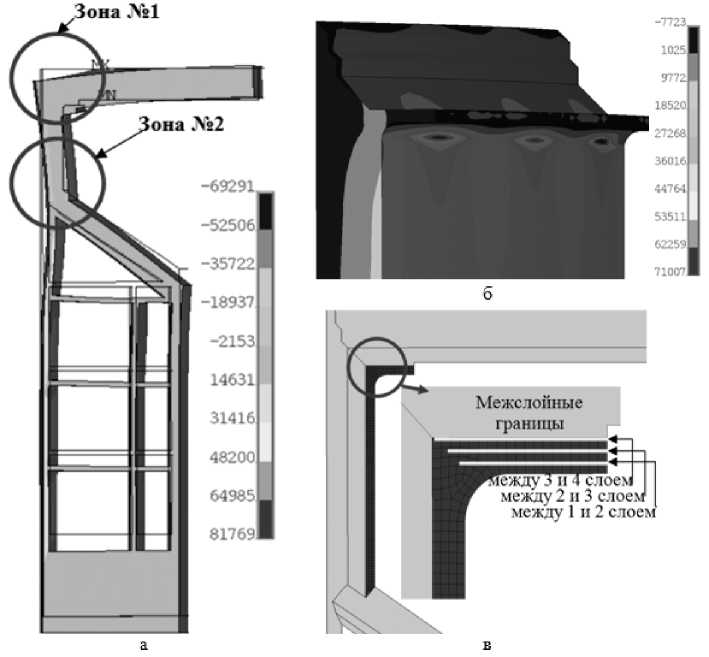
Рис. 3. Осевые напряжения σ zz (Sy) (Па) полного образца-сегмента (а) и его наиболее нагруженного участка (б)

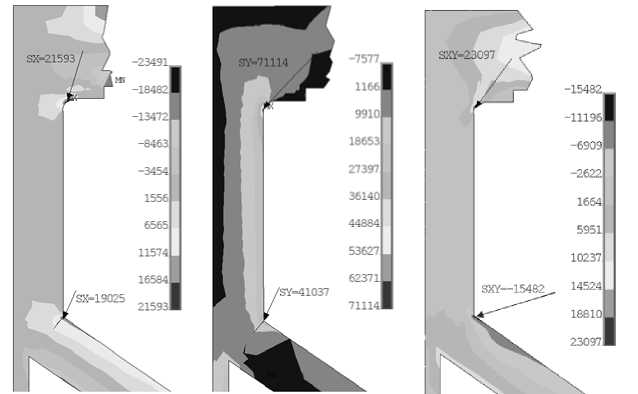
Рис. 4. Поля напряжений (Па) σ rr (Sx), σ zz (Sy) и σ rz (Sxy), в сечении, проходящем через центр отверстия

По результатам предыдущих исследований наиболее опасными, определяющими запас статической прочности фланца, являются межслойные напряжения, возникающие в зонах перегиба слоев внутри конструкции. Анализ межслойных напряжений проведен на основе полей осевых напряжений σzz(Sy), построенных в различных продольных сечениях образца-сегмента. Исследование показало, что наибольшие значения межслойные напряжения достигают в сечении, проходящем через центр отверстия (рис. 3). Максимальные напряжения возникают на границе между 1 и 2 слоями вблизи точки перегиба слоев в зоне №1. В качестве примера на рис. 4 показаны поля осевых, радиальных и радиально-осевых напряжений, построенные в сечении, проходящем через центр отверстия. Данные напряжения эквивалентны нормальным и касательным межслойным напряжениям для торцевого и цилиндрического участков фланца соответственно. На рис. 5 приведены эпюры межслойных напряжений между первым и вторым, а также вторым и третьим слоями (расположение границ показано на рис.3, в).

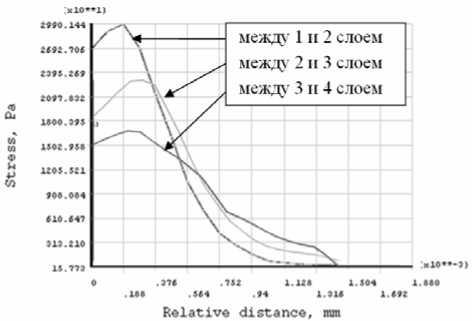
а

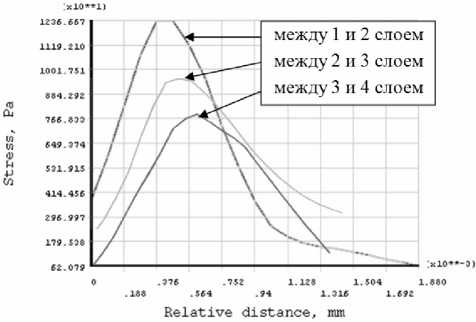
б

Рис. 5. Эпюры межслойных напряжений (Па) σzz(Sy) (а) и σrz(Sxy) (б) в сечении, проходящем через центр отверстия

Для оценки прочности фланца использовался критерий максимальных напряжений для трех возможных механизмов разрушения: разрыв вдоль основы и утка, расслоение от межслойного сдвига и расслоение вследствие нормальных напряжений отрыва слоев. Пределы прочности материала [4], максимальные напряжения в образце при единичной нагрузке и оценки предельной нагрузки для образца, соответствующей различным механизмам разрушения, приведены в таблице 1. Анализ результатов расчетов показывает, что усилие нагружения, вызывающее расслоения образца-сегмента, определяется напряжениями поперечного межслойного отрыва и равняется 4300 Н для образца.

Для проверки результатов расчетов были проведены сравнения с результатами испытаний на растяжение пяти образцов-сегментов, проведенных в лаборатории Института механики сплошных сред УрО РАН. Испытания показали, что образцы разрушаются по механизму расслоения. Зона расслоения приблизительно соответствует расчетной, на рис 6, а, б показан характерный вид расслоения одного образца. После начала расслоения наблюдалось падение нагружающего усилия до полного разрыва армирующих слоев (рис. 6, в). Таким образом, предельная несущая способность исследуемого образца может оцениваться по нагрузке, соответствующей началу расслоения. Значение разрушающей нагрузки для образцов характеризовалось значительным разбросом в диапазоне 3066-6978 Н. При этом все образцы имели технологические дефекты структуры материала: складки слоев, смоляные карманы, расслоения.

Таблица 1. Оценка прочности образца-сегмента по результатам численного моделирования

Вид предполагаемого разрушения	Предел прочности материала, МПа	Максимальные расчетные напряжения, МПа	Предельная нагрузка, Н
разрыв вдоль осно-вы/утка	600/300	71,114∙10-3 (в зоне перегиба слоев)	24 000/12 000
расслоение от межслоевого сдвига	45	12,237∙10-3 (в зоне перегиба слоев)	10 500
расслоение от напряжений отрыва	45	29,901∙10-3(в зоне перегиба слоев)	4 300

Кроме того, образцы имели ряд отклонений по толщине слоев, а также нарушения плоскостности опорных поверхностей. Для корректировки последнего отклонения при установке образца в испытательную оснастку применялась затяжка болтов, что приводило к дополнительному нагружению образца и дополнительному отличию получаемых в эксперименте полей напряжений и деформаций от расчетных значений. Эти обстоятельства, по-видимому, и обуславливают большой разброс предельной нагрузки, получаемой при испытании образцов. Однако среднее значение предельной нагрузки для образца - 4700 Н отличается от расчетного значения менее чем на 10%.

а)

в

Рис. 6 . Фото зоны разрушения первого образца-сегмента при механических испытаниях

Выводы: сравнение результатов моделирования с данными натурных испытаний образцов-сегментов показывает, что математическая модель позволяет достаточно точно определить наиболее опасную зону, механизм разрушения фланца – расслоения вследствие высоких растягивающих напряжений, а также среднее значение предельной нагрузки для образца. Для уточнения предельной нагрузки возможна корректировка разработанной расчетной модели с учетом дефектов структуры материала и геометрии образца, а также его предварительного нагружения, возникающего при затяжке болтов. Однако следует отметить, что напряженное состояние образца-сегмента при испытаниях несколько отличается от напряженного состояния полноразмерной конструкции кожуха при эксплуатационных нагрузках. Для окончательного подтверждения её несущей способности необходимо проведение аналогичного расчета и анализа напряженно-деформированного состояния с выявлением в конструкции областей наибольших межслойных напряжений и оценкой запасов прочности по критериям, апробированным в настоящей работе.