Моделирование механического взаимодействия полимерной нанопленки с наноиндентором
Автор: Гаришин О.К., Лебедев С.Н.
Статья в выпуске: 15, 2007 года.
Бесплатный доступ
В работе предлагается способ определения упругих констант полимерных нанопленок на основе данных, полученных с помощью атомно-силовой микроскопии. При расчетах предполагали что исследуемый "образец" представляет собой высокоэластичный чисто упругий материал. Известно, что при внедрении наноиндентора в образец, деформации вблизи контакта могут достигать десятков и даже сотен процентов. Поэтому, в первом приближении было принято, что механические свойства материала описываются Нео-Гуковым упругим потенциалом. Более сложные свойства, такие как пластичность и вязкоупругость в данной работе не рассматривались. Получены расчетные зависимости между силой действующей на индентор, глубиной его проникновения в пленку, толщиной пленки и ее механическими константами. Эти результаты представлены в виде эмпирических аппроксимационных формул (с точностью 90%). С их помощью, зная толщину нанопленки и получив с помощью атомно-силовой микроскопии зависимость между силой и глубиной внедрения можно рассчитать упругие свойства материала.
Короткий адрес: https://sciup.org/146211298
IDR: 146211298 | УДК: 539.3
Текст научной статьи Моделирование механического взаимодействия полимерной нанопленки с наноиндентором
Numerical dependences between force applied to indenter, depth of its penetration into a film, thickness of a film and its mechanical constants are received. These results are submitted as empirical approximation formulas (with accuracy of 90 %). With their help, knowing nanofilm thickness and having received with the help of atomic-force microscopy dependence between force and depth of introduction it is possible to calculate elastic properties of a material.
В настоящее время экспериментально установлено, что в дисперсно наполненных полимерных композитах около частиц наполнителя существуют слои связующего с отличными от остальной матрицы механическими свойствами. Причем в случае нанодисперс-ного наполнителя объемная доля слоев достигает значений, соизмеримых с общим объемом связующего (из-за очень большой площади поверхностей раздела фаз). Именно эти слои в значительной степени определяют особенности механического поведения наноматериала, его упругость, деформации в момент разрушения, прочность. На границе полимера с внешней средой также имеются нанослои, которые активно участвуют в формировании сил поверхностного натяжения, адгезионных свойств при контактах с другими материалами, проницаемости границы в задачах тепло- и массообмена и т.д. Именно на границе с внешней средой интенсивно идет старение полимера и обычно начинается разрушение изделия. Этим объясняется актуальность проблемы исследования нанослоев, появляющихся на границах раздела фаз и на внешней поверхности композита.
Кроме того, современная техника и применение высоких технологий для модификации поверхностных слоев позволяют формировать пленки и покрытия, в том числе наноразмерные, которые обладают уникальным сочетанием свойств, принципиально отличающимся от сочетания свойств материалов, обработанных традиционными методами. Внедрение нанотехнологий требует измерения физических и механических свойств применяемых материалов на субмикронном и нанометровом уровне.
Методы наноиндентации - анализ механического отклика поверхности образца на вдавливание наносенсора атомно-силового микроскопа (АСМ) - широко применяются в настоящее время для определения механических свойств материала на малых масштабах измерения [1-6], а также для непосредственного наблюдения таких явлений, как появление дислокаций, возникновение сдвиговой нестабильности, фазовых переходов и т.д. Эти технологии открывают новые горизонты для понимания тех структурных механических и физических процессов, которые происходят в материале на наноуровне.
Атомно-силовая микроскопия позволяет получать информацию о геометрии поверхности и механических свойствах материала, но для расшифровки получаемой в экспериментах информации необходимо строить математические модели. Одна из таких моделей и предлагается ниже.
Для того чтобы определить, какими механическими свойствами обладает исследуемый материал, надо знать связь между силой реакции на наносенсоре и глубиной его проникновения в поверхность. Имея решение соответствующей краевой задачи, можно по данной экспериментальной зависимости определить механические константы среды.
Контактную задачу о внедрении наносенсора (зонда) атомносилового микроскопа в полимерную пленку с неизвестными механическими свойствами решали в нелинейно-упругой осесимметричной постановке (рис. 1). При расчетах радиус вершины зонда R брали равным 10 и 20 нм, α = 20°. Модельные образцы представляли в виде круглых «таблеток» с одинаковым радиусом RL = 200 нм, но с разной толщиной H, которую варьировали от 5 до 100 нм.
Считали, что зонд является абсолютно жестким телом, а механическое поведение нанопленки можно описать с помощью Неогу-кового потенциала,
W = C ( tr B - 3 ) , (1)
где C 1 – половина начального модуля сдвига, B – левый тензор Коши– Грина в полярном разложении деформационного градиента среды. Сверху на индентор действовала сосредоточенная сила F z . На границе контакта зонда и образца выполнялось условие полного прилипания без проскальзывания в процессе нагружения. Нижняя граница образца находилась в полном контакте (без отрывов и проскальзывания) с абсолютно жесткой плоскостью. Задачу решали методом конечных элементов.
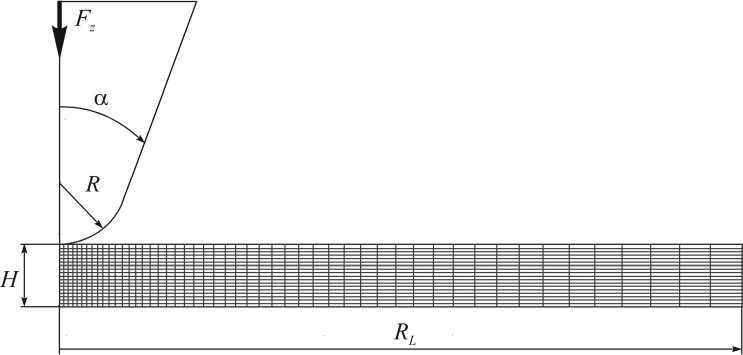
Рис. 1. Расчетная схема конечно-элементной осесимметричной задачи о внедрении наносенсора атомно-силового микроскопа в полимерный образец
В качестве иллюстрации расчетов на рис. 2 и 3 приведены распределения полей гидростатических напряжений и интенсивности напряжений (все отнесено к константе Трелоара C 1 ) для случая, когда толщина нанопленки равна 18 нм, а радиус вершины зонда – 20 нм.
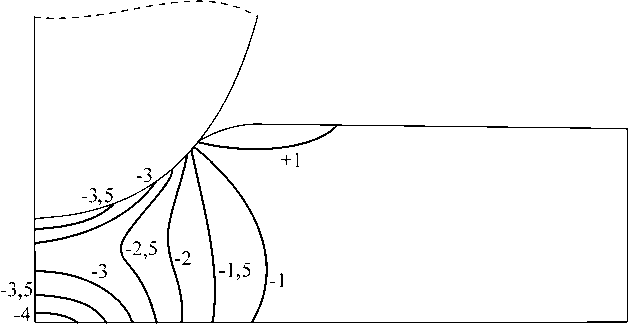
Рис. 2. Распределение гидростатических напряжений σ 0/ C 1 для случая H = 18 нм (индентор внедрен на 8,3 нм)
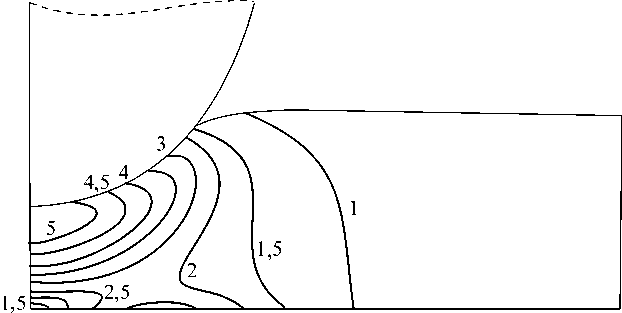
Рис. 3. Распределение интенсивности напряжений σ int / C 1 для случая H = 18 нм (индентор внедрен на 8,3 нм)
На рис. 4 представлены зависимости силы реакции F z , действующей на щуп от глубины его проникновения в материал u z . Приведены зависимости для образцов с различной толщиной Н . Из графиков видно, что чем больше значение Н , тем меньшие усилия требуются для внедрения индентора на одну и ту же величину.
Это и понятно, так как в более тонких образцах сильнее «чувствуется» влияние жесткой нижней границы, т.е. чем тоньше слой, тем более жесткой является рассчитываемая конструкция. Следует отметить, что на начальном этапе деформирования параметр Н практически не влияет на вид расчетных кривых – все они лежат поблизости друг от друга.
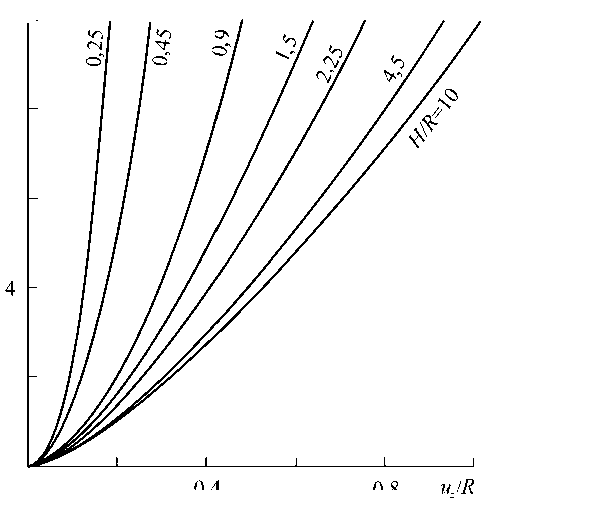
Рис. 4. Зависимости силы реакции Fz , действующей на щуп, от глубины его проникновения в материал uz : Н – толщина образца, R – радиус вершины щупа, С 1 – упругая константа потенциала Трелоара
Данные зависимости были аппроксимированы формулой (2) (с точностью, примерно, 90 %). Таким образом, зная толщину нанопленки и получив с помощью атомно-силовой микроскопии зависимость F z (u z ), можно достаточно просто определить упругий модуль материала,
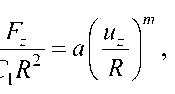
где
a = 4
m =
14,90 ( H/R )- 2,4 + 13,82,
20,45 ( H/R )- 1,525 + 9,00,
' 0,82 exp ( - 1,56 H/R + 0,29 ) + 1,448,
- 0,0129 H/R + 1,5085,
0,25 < H/R < 0,90,
0,90 < H/R < 10,0, 0,25 < H/R < 2,25, 2,25 < H/R < 10,0.
Работа выполнена при поддержке Российского фонда фундаментальных исследований и Министерства промышленности и природопользования Пермского края (Гранты № 07-08-96016-р_урал_a, № 07-08-96017-р_урал_a).


