Моделирование метано-водородного пламени на примере вихревой горелки

Выбрасываемые в атмосферу продукты сгорания углеводородных топлив, используемых в энергетических и транспортных установках, являются основным источником парниковых газов, приводящих к повышению температуры окружающей среды, что ведет к глобальному изменению климата на Земле. В связи с этим в последнее время в мире уделяется большое внимание вопросу снижения выбросов углекислого газа авиационными газотурбинными двигателями и промышленными газотурбинными установками.

Использование метано-водородного топлива позволяет в разы снизить эмиссию СО2 в атмосферу. При этом использование водорода в топливной смеси приводит к ряду дополнительных эффектов. Добавление водорода в топливно-воздушную смесь, с одной стороны, позволяет увеличить границу устойчивой работы двигателя, а, как известно, сжигание более «бедных» смесей приводит к снижению образования оксидов азота NOx. С другой стороны – при добав- лении водорода в топливо из-за его более высокого тепловыделения происходит возрастание температуры во фронте пламени и увеличение скорости его распространения, что увеличивает выбросы NOx и может привести к прогару элементов установки [1]. Поэтому при разработке горелочных устройств и камер сгорания необходимо детальное исследование различных режимов горения метано-водородных пламен.

В последние годы для решения задач горения широко используются методы вычислительной гидродинамики. Однако в настоящее время математические модели горения метановодородного топлива применительно к вихревым пламенам, реализуемым в камерах сгорания, недостаточно верифицированы.

В представленном исследовании для расчета закрученного турбулентного метановодородного пламени разработана комплексная численная методика, аккуратно учитывающая турбулентность, сложный теплообмен, в том числе радиационный, включающая модель горения с достаточно детальными кинетическими механизмами и адекватным учетом взаимодействия термохимических процессов с турбулентностью.

Богатый опыт авторов моделирования широкого класса пламен [2–5] позволил сразу остановиться на вихреразрешающей LES модели турбулентности для расчета структуры сильно закрученного потока, реализуемого в камерах сгорания модели дискретных ординат с WSSG для расчета радиационного переноса в высокотемпературных газовых пламенах.

В работе [6] авторов статьи проведен сравнительный расчетный анализ механизмов реагирования и моделей турбулентного горения на задаче струйного диффузионного горения метано-водородной смеси. В итоге, для закрученного метано-водородного пламени предложено использовать следующую математическую модель.

Математическая модель

Для многокомпонентных реагирующих течений необходимо решение уравнений сохранения массы, импульса, энергии, переноса газовых компонент и уравнений переноса для турбулентных характеристик потока:

^P + V- ( p v) = 0. d t

Выражение представляет собой общий вид уравнения сохранения массы и применимо как для несжимаемых, так и сжимаемых потоков.

Сохранение импульса в инерционной системе отсчета описывается уравнением

d .       ..                  ^ ^

— (pv) + V - (pvv) = -Vp + V - (t) + pg + F, dt где p - статическое давление; т - тензор напряжений, описанный ниже; а pg и F - соответственно сила гравитации и внешняя массовая сила.

Тензор напряжений имеет вид т = ц

( V . + V v T ) - 3 V- vI

где ц - молекулярная вязкость; I - единичный тензор. Второй член в правой части описывает эффект объемного расширения.

Для сильно закрученных турбулентных течений, которые реализуются в вихревых горелках, по оси факела формируются зоны обратных течений с прецессией вихревого ядра. Использование простых RANS моделей турбулентности для моделирования таких течений приводит к некорректным результатам, поэтому в работе при расчете турбулентных характеристик потока применялся метод крупных вихрей (LES), при котором крупные вихри разрешаются напрямую [6], а мелкие – моделируются с помощью модели подсеточной вязкости. Cоставляющие тензора подсеточных напряжений тij определяются из соотношения, похожего на соотношение Буссинеска для RANS моделей турбулентности,

^т j - 1 ^т kk b ij = 2 Ц t S,

здесь S_{i , j} – тензор скоростей деформации

S

¹j = 2

(д й дй.}

+ j д xj дxi)

Для вычисления подсеточной вязкости µ _t в ходе данной работы использовалась модель WALE (Wall-Adapting-Local-Eddy-Viscosity) [7]. Вихревая вязкость в этой модели вычисляется как

Ц т = Р Ls ²

( S i^d , j S i^d , j ) ^3/2

( S i, j S i,j)^5/2 + ( s ^ j + s ^ . ) ⁵/⁴’

где L_s и S_i ^d _{, j} определяются как

L s = min( kd , C w V ^1/3 ),

d ¹ / _2 , 2 \ ¹ e “² “ ^{д u}i

^Si ^, j = 2 ( ^gi ^, J ^{+ g}J ^, i ) 3 ^ i ^, J^gk , k ^gi , j = д X j ’

где k = 0,41 – это константа фон Кармана; C w = 0,325.

Для учета теплообмена решается уравнение сохранения энергии в следующем виде:

- ( p E ) + V- ( v ( p E + p )) = V-д t

(              ^

k eff V T - X h j J j + ( т- v ) + S h

j

где k eff – эффективный коэффициент теплопроводности ( k + k t ), где k t – коэффициент турбулентной теплопроводности, определяемый моделью турбулентности; J_j – диффузионный поток компоненты j . Первые три члена правой части уравнения описывают перенос энергии за счет теплопроводности, диффузии компонент и вязкой диссипации соответственно, S h – источник тепла за счет теплоты химических реакций и других механизмов.

Учет радиационного теплообмена осуществляется с использованием модели дискретных ординат (DO) [8]. Модель решает уравнение радиационного теплообмена для конечного числа дискретных телесных углов, каждый из которых связан с вектором направления s, фиксированным в глобальной декартовой системе (x, y, z). Модель позволяет контролировать точность угловой дискретизации, при этом решается количество уравнений переноса равное количеству заданных направлений. Метод решения идентичен тому, который используется для уравнений течения жидкости и энергии.

Выбор модели коэффициента поглощения среды для уравнения радиационного теплообмена является отдельной большой задачей при моделировании лучистого теплообмена. Моделей расчета коэффициента поглощения достаточно много, от детальных и трудоемких подходов до грубого приближения. Хорошо зарекомендовавшим подходом для задач турбулентного горения является метод взвешенной суммы серых газов (WSGGM) [9]. В этой модели спектральная зависимость коэффициента поглощения газа представляется в виде суммы взвешенных серых газов.

Для моделирования турбулентного горения в работе применялся подход частично перемешанного горения с моделью FGM (Flamelet Generated Manifolds) [10]. Достоинством такого метода является то, что он позволяет использовать кинетические механизмы реагирования с большим количеством реакций, время расчета при этом возрастает не столь значительно, как, например, при использовании модели Eddy Dissipation Concept (EDC). При нестационарных LES расчетах применение flamelet-методик на сегодняшний день единственная возможность применять детальные кинетические механизмы с приемлемыми вычислительными затратами, а модель FGM является одной из самых современных широко используемых моделей.

Модель ламинарных флэймлетов предполагает, что пламя – это ансамбль ламинарных флэймлетов, которые имеют внутреннюю структуру, существенно не меняющуюся под действием турбулентности. Эти ламинарные флэймлеты объединяются в турбулентное пламя с помощью статистического усреднения. Модель Flamelet Generated Manifolds (FGM) предполагает, что скалярная эволюция (т. е. реализованные траектории на термохимическом многообразии) в турбулентном пламени может быть аппроксимирована скалярной эволюцией в ламинарном пламени. И в модели ламинарных флэймлетов и модели FGM все компоненты и температура параметризуются несколькими переменными, такими как доля смеси, скалярная диссипация и/или прогресс реакции. Уравнения на эти переменные решаются в ходе трехмерного CFD расчета, а локальные значения температуры, компонентный состав смеси и ее свойства восстанавливаются, используя заранее насчитанные таблицы флэймлетов. Модель FGM фундаментально отличается от модели ламинарных флэймлетов. Например, поскольку ламинарные флэймлеты параметризуются деформацией, термохимия всегда стремится к химическому равновесию, та как скорость деформации уменьшается к выходу из камеры сгорания. В отличие от этого, модель FGM параметризуется переменной прогресса реакции и пламя может быть полностью погашено, например, путем добавления воздуха. FGM не делает никаких предположений о тонких и неповрежденных флэймлетах, и модель теоретически может быть применена к пределу перемешанного реактора, а также моделированию воспламенения и гашения.

Приведенные уравнения всех моделей решаются посредством численных методов, реализованных на основе метода контрольных объемов, использующего неструктурированные расчётные сетки. Расчетная сетка строится на базе детальной твердотельной CAD-модели, учитывающей реальную пространственную геометрию исследуемого объекта. Для связи поля скорости и давления используется метод SIMPLEC. Аппроксимация членов уравнений переноса производится с применением схем второго порядка точности по пространству и времени. Численная методика позволяет проводить распределенные вычисления с применением технологии MPI с хорошей эффективностью при распараллеливании на большое количество вычислительных ядер.

Моделирование закрученного метано-водородного пламени

В работе [11] сотрудниками кафедры теплотехники и тепловых двигателей Самарского национального исследовательский университета представлен обзор перспективных метановодородных кинетических моделей горения. Предложен вариант модифицированного химикокинетического механизма Wang 2018 (48 компонентов и 308 реакций [12]. Показано, что математическая модель горения метано-водородных смесей с удовлетворительной точностью предсказывает границы срыва и проскока пламени вверх по потоку, наблюдаемых в модельном горелочном устройстве, и может использоваться для определения границ устойчивой работы разрабатываемых камер сгорания газотурбинных установок при их переводе на водородосодержащие смеси.

В работе [13] специалистами Института химической кинетики и горения СО РАН на основе подробной модели AramcoMech 2.0 [14] представлены два сокращенных кинетических механизма с различными уровнями детализации для горения смесей CH 4 /H 2 : RMech1 (30 компонент и 70 реакций) и RMech2 (21 компонента и 31 реакция), которые хорошо описывают кинетику горения одномерных пламён в условиях характерных для камер сгорания.

Тестирование предложенных математических моделей и кинетических механизмов горения метано-водородной смеси ранее было выполнено авторами на задаче струйного диффузионного горения [6]. Показано хорошее соответствие результатов моделирования данным экспериментов, выполненных DLR (немецкий центр аэрокосмических исследований и технологий) [15–17].

В настоящей работе рассмотрено распространение закрученного пламени метановодородной смеси от вихревой горелки Sydney Swirl Burner. Схема данного горелочного устройства представлена на рис. 1.

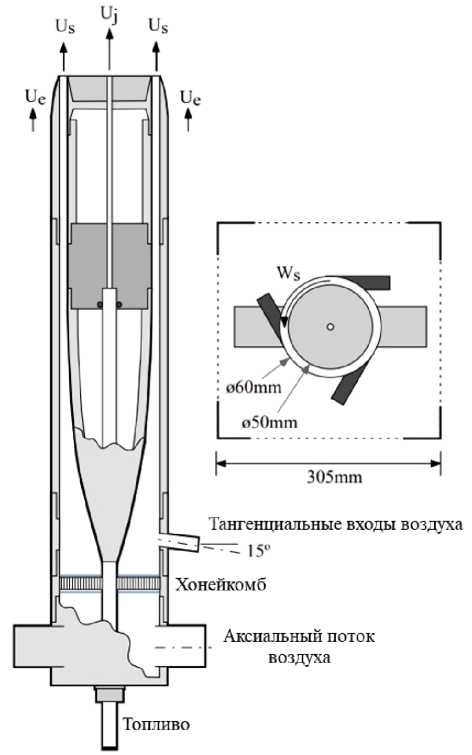
Рис. 1. Схема вихревого горелочного устройства Sydney Swirl Burner

Fig. 1. Schematic of the Sydney Swirl Burner

Устройство отличается простотой конструкции с чётко определёнными граничными условиями, но при этом создаёт сложные завихрённые потоки, мало чем отличающиеся от потоков, наблюдаемых в реальных камерах сгорания.

Данные экспериментов по данному горелочному устройству приведены в [18; 19].

На начальном этапе моделирования горелки был рассмотрен режим изотермического течения воздуха N29S054 со следующими параметрами:

• –    скорость центральной струи U j = 66 м/с;

• –    скорость закрученного коаксиального потока U s = 29,74 м/с, параметр крутки 0,54;

• –    скорость внешнего потока воздуха U e = 20 м/с.

Для задания аксиальной скорости центральной струи использовался турбулентный профиль, согласно степенному закону [20],

UU} = C o U j 1 -

1/7

1.01 • r ,

Рис. 2. Расчетная сетка в центральном сечении, 1,5 млн ячеек

где C 0 = 1,218 и r j = 1,8 мм. Для коаксиального канала аксиальная и тангенциальная компоненты скорости задавались с помощью аналогичного выражения.

Расчеты выполнялись в полной пространственной постановке, диаметр расчетной области 0,13 м, длина 0,35 м. Использовалось два вида неструктурированной расчетной сетки – базовая с 1,5 млн расчетных ячеек и более детальная сетка с 4,9 млн расчетных ячеек. На рис. 2 приведен пример расчетной сетки для варианта с 1,5 млн ячеек, а также показана линия среза горелки и линии на расстояниях 20 и 70 мм, для которых проводилось сравнение результатов расчета и экспериментальных данных. Расчеты выполнялись в нестационарной постановке с шагом по времени 5·10–5 с. Для получения осредненных полей в ходе расчета проводилось осреднение величин по времени в течение 1 с физического времени процесса.

На рис. 3 приведена картина течения, формируемая вихревой горелкой, показаны мгновенное и осредненное поля скорости. Видно, что в центральной области закрученного течения формируется сильное возвратное течение, которое будет способствовать интенсивному перемешиванию газов, хорошему воспламенению и устойчивому горению смеси. На рис. 4, 5 представлено сравнение результа

Fig. 2. Computational mesh in the central section, 1.5 million cells

тов расчета и данных эксперимента для компонент осредненной скорости и пульсаций скорости потока на разных расстояниях от среза горелки. Из рисунков видно, что используемая LES WALE модель турбулентности позволяет, даже на относительно грубой расчетной сетке получить хорошие результаты не только для средних характеристик течения, но и для пульсационных, что важно для моделирования процесса горения.

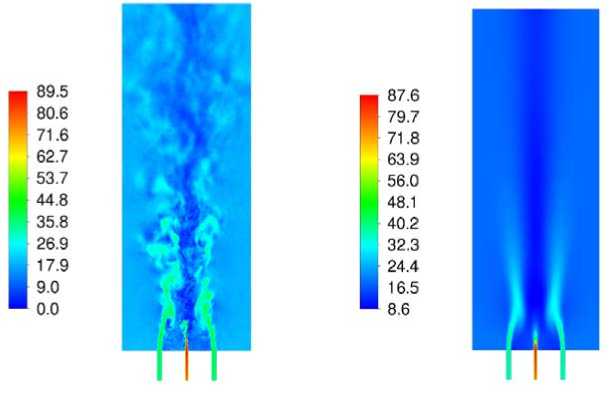
а                                  б

Рис. 3. Картина течения: а – мгновенное поле скорости, м/с; б – осредненное поле скорости, м/с

• Fig. 3.    Flow structure: a – instantaneous velocity field, m/s; б – mean velocity field, m/s

  
  
  
  
  
  
  

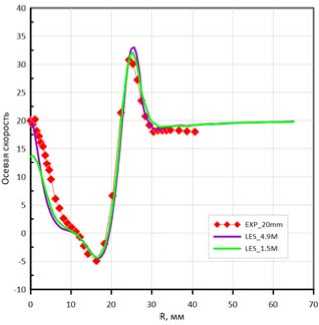
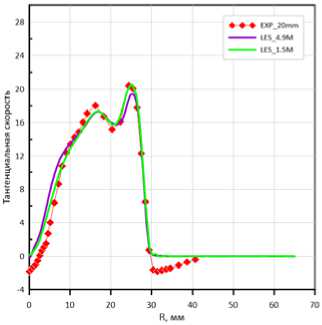
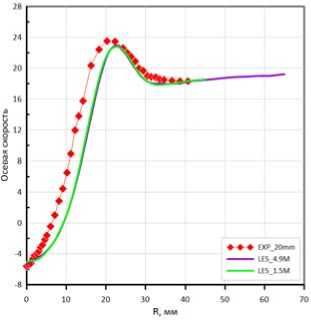
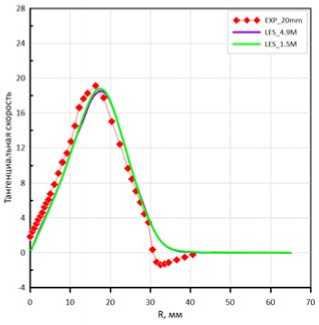
  Рис. 4. Компоненты скорости, м/с:

  
  
  
  
  

  б

  
  

  а – на расстоянии 20 мм

  
  

от среза горелки; б – на расстоянии 70 мм от среза горелки

• Fig. 4.    Velocity components, m/s: а – at a distance of 20 mm from the nozzle; б – at a distance of 70 mm from the nozzle

  
  
  
  

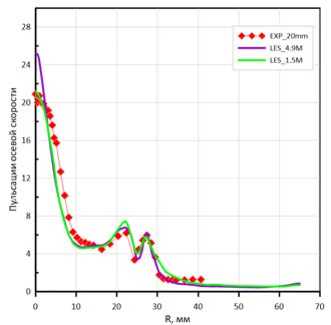
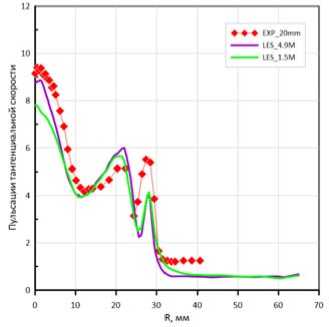
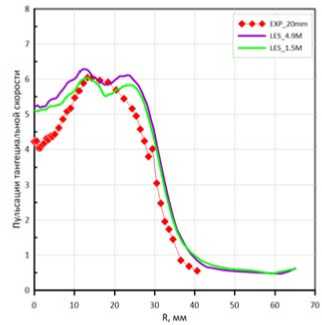
  Рис. 5. Компоненты пульсации скорости:

  а – на расстоянии 20 мм от среза горелки; б – на расстоянии 70 мм от среза горелки (Начало)

  
  

• Fig. 5.    Velocity pulsation components:

а – at a distance of 20 mm from the nozzle; б – at a distance of 70 mm from the nozzle (Beginning)

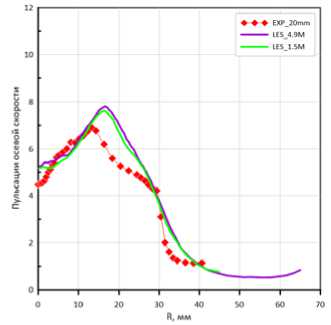
Рис. 5. Окончание

б

Fig. 5. Ending

б

д

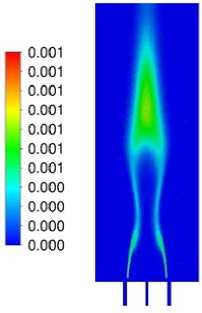
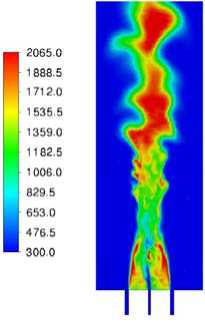
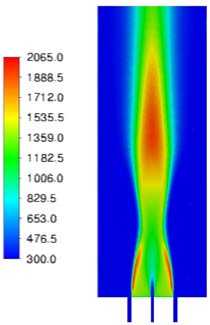
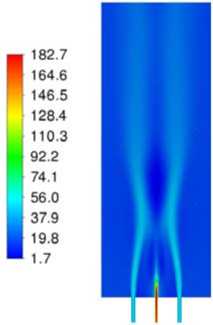
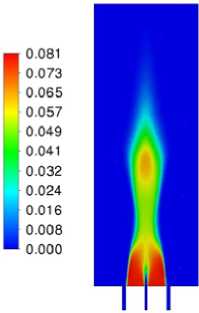
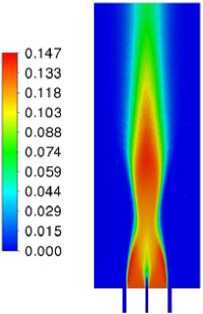
Рис. 6. Результаты моделирования горения метано-водородной смеси в вихревой горелке: а – мгновенное поле температуры, K; б – осредненное поле температуры, K; в – осредненное поле скорости м/с; г – осредненное поле массовой доли CO; д – осредненное поле массовой доли H 2 O; е – осредненное поле массовой доли OH

• Fig. 6.    Results of modeling the combustion of a methane-hydrogen mixture in a swril burner: а – instantaneous temperature field, K; б – mean temperature field, K; в – mean velocity magnitude m/s;

г – mean mass fraction of CO; д – mean mass fraction of H₂O; е – mean mass fraction of OH

Далее было проведено моделирование горения метано-водородной смеси (режим SMH1) для условий, заданных в эксперименте [14].

Соотношение метана к водороду в топливе 1:1.

Скорость топлива U j = 140,8 м/с.

Скорость закрученного коаксиального потока воздуха U s = 42,8 м/с, параметр крутки 0,32.

Скорость внешнего потока воздуха U_e = 20 м/c.

При моделировании турбулентного горения использовалась модель FGM c кинетическим механизмом RMech1.

Для задания граничных условий для скорости газов на входах использовались те же профили со степенным законом, что и для изотермической задачи.

Из-за высоких вычислительных затрат моделирование горения проводилось только на грубой расчетной сетке в 1,5 млн ячеек. Моделирование выполнялось на доступных вычислительных мощностях (44 расчетных ядра). Для расчета одного варианта с учетом осреднения требовалось около 100 ч машинного времени.

На рис. 6–8 представлены результаты моделирования.

На рис. 6 показаны характерные распределения температуры, скорости и массовых долей газовых компонент в пламени вихревой горелки.

Из графиков, представленных на рис. 7, 8, видно, что модель в целом качественно воспроизводит поля температуры и концентрации газовых компонент, что позволяет рекомендовать ее для использования при разработке и проектировании камер сгорания ориентированных на сжигание перспективных топлив на основе метано-водородных смесей.

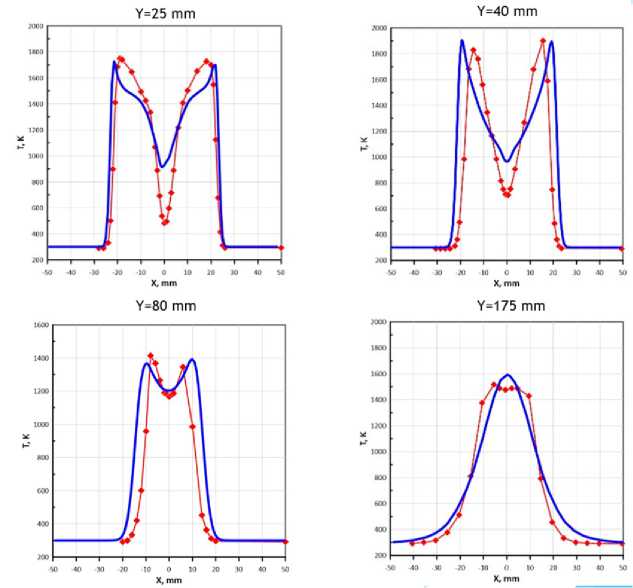
Рис. 7. Графики температуры на разном удалении от среза сопла, K. Красные точки – эксперимент, сплошная синяя линия – расчет

Fig. 7. Temperature at different distances from the nozzle, K.

Red dots – experiment, solid blue line – calculation

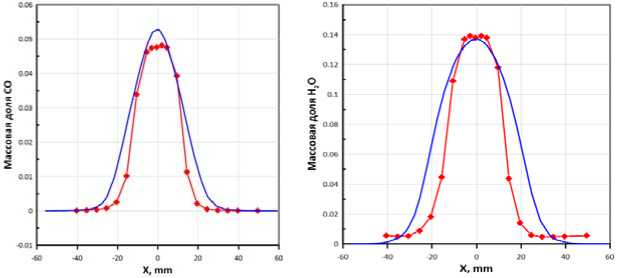
Рис. 8. Графики газовых компонент на расстоянии 175 мм от среза сопла. Красные точки – эксперимент, сплошная синяя линия – расчет

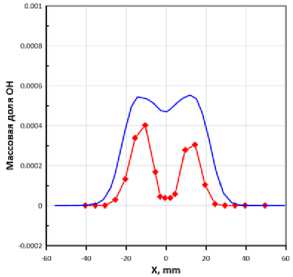
Fig. 8. Species mass fractions at 175 mm from the nozzle.

Red dots – experiment, solid blue line – calculation

Заключение

Представлена математическая модель для расчета закрученных метано-водородных пламен, основанная на использовании LES модели для описания турбулентности, FGM модели горения с кинетическим механизмом реагирования RMech1, DO модели радиационного переноса.

Сравнение результатов расчетов с экспериментальными данными показало, что выбранные математические модели процессов турбулентной аэродинамики, тепломассообмена и химического реагирования, а также алгоритмы расчета позволяют с достаточной для инженерной практики точностью моделировать горение метано-водородных смесей в закрученных потоках, формируемых вихревыми горелочными устройствами, широко используемыми в камерах сгорания газотурбинных установок.

Вычислительные затраты, необходимые для проведения подобных расчетов, являются относительно приемлемыми при использовании доступных кластерных систем.

Acknowledgements. This work was supported by the Ministry of Education and Science of Russian Federation, Agreement from 24.04.2024 № 075–15–2024–543.