Моделирование метода измерения диэлектрической проницаемости плоских образцов на основе кольцевых резонаторов

Измерение диэлектрической проницаемости является сложной и неоднозначной задачей. Рассмотрим один из методов основанный на кольцевом полосковом резонаторе на диэлектрической подложке [1]. Такой резонатор показан на рис.1.

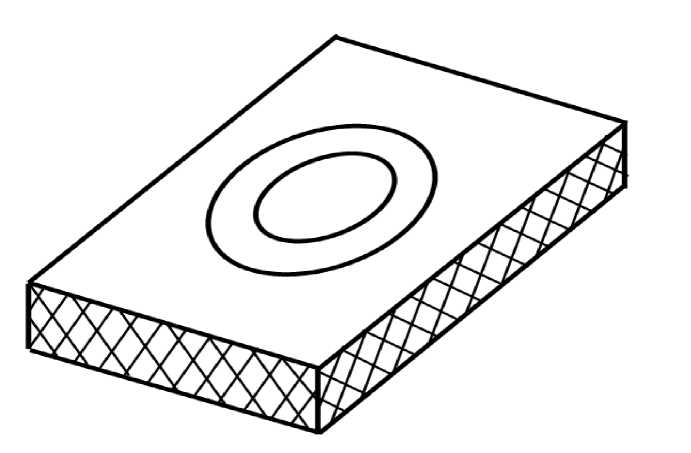
Рис. 1. Кольцевой полосковый резонатор

Предложенный метод измерения является неразрушающим методом контроля диэлектрических плоских (ДП) материалов в СВЧ диапазоне, основанный на измерении резонансной частоты кольцевого полоскового резонатора на несимметричной полосковой линии (НПЛ) при внесении в его поле рассматриваемого материала.

На рисунке 32показана схема устройства для измерения и контроля ДП предлагаемым методом. Расчет рассматриваемой схемы основан на известных соотношениях теории полосковых структур [1,2].

Эффективная диэлектрическая проницаемость несимметричной полосковой линии резонатора без вносимого диэлектрика определяется , с одной стороны, из условия резонанса, и для колебания E₁₁₀ находится по формуле [1,3]:

eэф

ц р 0 ^{Ч u} 11 ч_ч

ч

P dcp Ш

где d_ср ≈ 2R - средний диаметр резонатора.

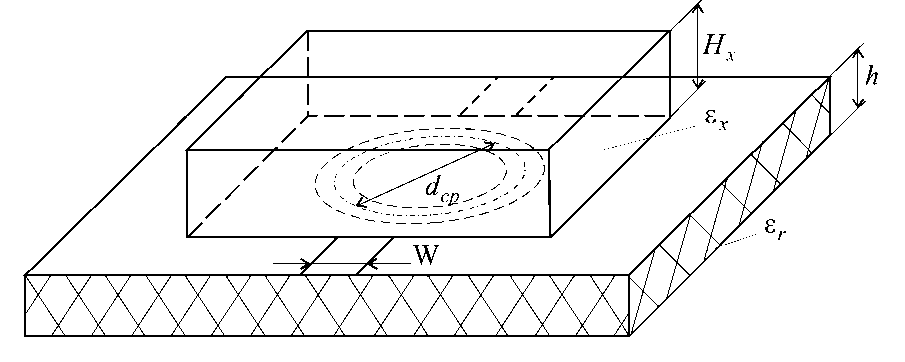
Рис.2. Устройство для измерения диэлектрической проницаемости подложки

А с другой стороны при равенстве толщины резонатора толщине подводящей линии W резонансную частоту приближенно можно посчитать по формуле [3]:

Те д — е + 1 + эф     r

e r -   ¹

M

где

M =

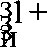
12 h ц 2

W чш.

Приравнивая правые части равенств (1) и (2) получаем соотношение для расчета диэлектрической проницаемости подложки резонатора

er

p 0

2 _u ц _{2 M} 11

p d_cp Ш M + 1 M + 1

.

Последнее соотношение справедливо для случая нулевой толщины проводников несимметричной полосковой линии.

Когда на поверхность резонатора помещается исследуемый материал, диэлектрическая проницаемость которого необходимо измерить, резонансная частота смещается. При этом значение эффективной диэлектрической проницаемости двухслойной линии передачи может быть вычислено из условий резонанса на новой длине волны λ = λ _p1

e эфф

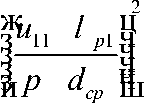
или, если известны значения ε _r и ε _x , то

e - e

^{2 е}эф = e r ⁺ e x ⁺ — •                   ⁽⁵⁾

Последняя формула справедлива для случая бесконечной толщины H исследуемого материала.

Разделим выражение (5) на (2), учитывая значение εэф из выражений

(1) и (4), соответственно, получим

2 жц зu11  lp1 ч зиp dcp ччш жц зu11 lp0чч

rx

г:

r

er + e M

er — ex

M

x

.

Учитывая, что X = с// , переходим от длин волн к частотам

2 p 0 ч ^ц

rx

r

e r - e x

M er - ex

M

,

где f - частота без образца, f - частота с образцом.

И, разрешая последнее уравнение относительно εx , получаем аналитическую зависимость, связывающую диэлектрическую проницаемость исследуемого материала с резонансными частотами устройства ex =(K

K  er ,

где

M + 1

K — ----

M - 1

На практике формулу (6) можно использовать для образцов конечной толщины вследствие экспоненциального затухания электромагнитной волны в направлении, перпендикулярном подложке. Минимальная толщина образца должна отвечать практически полному затуханию электромагнитной волны. Как показано в [2], это имеет место при условии, что толщина образца превышает толщину подложки не менее чем в пять раз. То есть H]h >  5 .

Процесс определения диэлектрической проницаемости состоит в измерении резонансной частоты кольцевого резонатора, вычислении диэлектрической проницаемости подложки e по формуле (3), измерении резонансной частоты f_p1 устройства при помещении на поверхность резонатора образца исследуемого материала и вычислении диэлектрической проницаемости этого материала по формуле (6). Экспериментальное исследование резонансных частот было проведено на панорамном измерителе ослаблений и КСВН Р2-61. Если известна e и h подложки кольцевого резонатора, то можно f p ₀ вычислить по формуле (6).

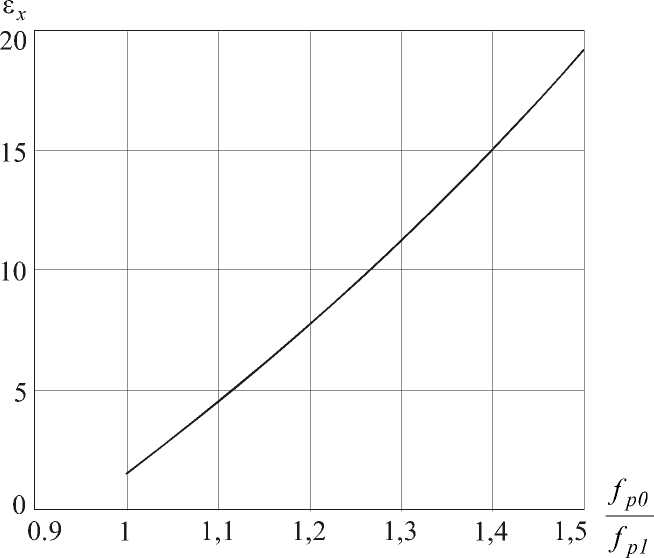
Рис. 3. Зависимость измеряемой диэлектрической проницаемости от относительного сдвига частоты

На рисунке 3 показана зависимость e от относительного сдвига f po I f_p1 при W = 3 мм , h = 1 мм ,  e_r = 5 .

Для практического определения резонансной частоты можно воспользоваться приближенной формулой:

где

рез

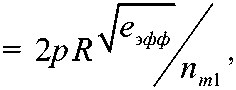
ж

R »0 . 875 b ^з з1+0 . 143 cos

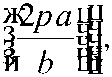
n - первый корень трансцендентного уравнения:

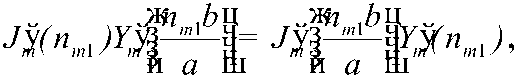
J ў( x )    и Y ў( x ) - производные функции Бесселя соответственно первого и второго рода m-го порядка.

a , b и ∆W - величины, показанные на рисунке 2

Из формулы (7) можно получить выражение для резонансной частоты:

f рез

Cnm1

2 pR e_эфф

где С -скорость света; R и ν m1 - определены выше.

Эффективную диэлектрическую проницаемость можно приближенно найти по формуле при W <

рез

ε

эф

й 1 к — КЕ_Г + 2 к ^r

ж      h ц 2 ъ

1 +(£r - W + 10 “8 ъ, зиwчшъ ъы

где h – высота подложки.

Была измерена диэлектрическая проницаемость подложки толщиной 4 мм и ε = 5 с помощью кольцевого резонатора по методике, описанной выше 3.1 – 1.2 на панорамном измерителе Р2-61.

Внутренний радиус кольцевого резонатора а =4мм, толщина кольца ∆W =3мм, толщина кольцевого резонатора h =1мм.

Измеряемая без подложки частота f_р0 равна 10.12ГГц, а резонансная частота резонатора f_р1 с измеряемым образцом равна 8.96.

Отношение ^р равно 1.16. По графику рисунка 3 находим, что этому ^fр1

значению соответствует диэлектрическая проницаемость e = 5 . 22 .

Измеренная диэлектрическая проницаемость ε = 5.12 отличается от номинальной ε_r = 5 на 6.4%.

Самой собой разумеется, что резонансы можно наблюдать по одному. Сначала, без образца, резонанс на частоте fр0  , а затем с образцом на частоте fр1 . Измерения проводились несколько раз и был выбран лучший результат.

Для подтверждения адекватности рассматриваемого метода было проведено моделирование установки в среде CST Microwave Studio. На рис. 4 показана установка для измерения проницаемости без образца.

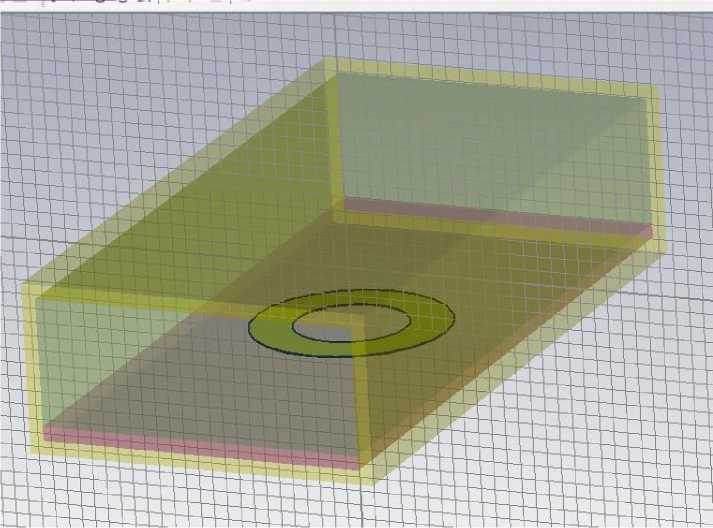
Рис. 4. Волновод с кольцевым резонатором на диэлектрической подложке

Определялся резонанс на кривой элемента матрицы рассеяния S 21 без образца и с образцом, как показано на рис.5.

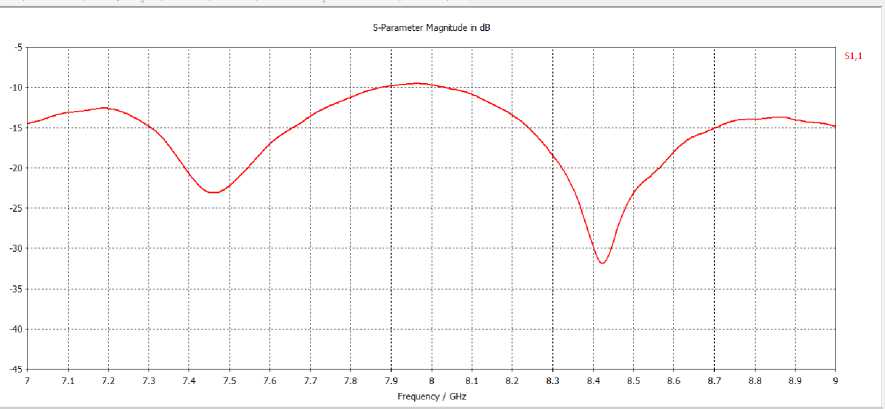
Рис. 5. Зависимость параметра S 21 от частоты кольцевого резонатора с измеряемой подложкой

Результаты моделирования системы с измеряемой подложкой были следующие: частота резонанса равна 9.3 ГГц. Отношение fo/fp1 для первой подложки = 1.13 (ε=5,) по графику рисунка 3 диэлектрическая проницаемость измеряемой подложки ε=4.91, что дает ошибку <5%.

Аналогично разместим над кольцевым резонатором диэлектрическую подложку с ε=12 и толщиной 4 мм. Проведем расчет составляющих матрицы рассеяния.

Резонансная частота сдвинется до 7.95 ГГц. Отношение fo/fp1 для второй подложки = 1.301 (ε=12,) по графику рисунка 3.3 главы 3 диэлектрическая проницаемость измеряемой подложки ε=12.1, что дает ошибку <5%.

Результаты моделирования достаточно хорошо согласуются с теоретическими и практическими результатами, полученными выше.