Моделирование методом Монте-Карло образования вторичных электронов в кристаллическом кремнии

Важной технической задачей в области электронно-лучевой литографии является определение разрешения экспонирования при заданной конфигурации системы. Конечное разрешение электронной литографии определяется не только размером сфокусированного пучка, а. также характером его взаимодействия с подложкой (слоем резиста). Столкновение электронов исходного пучка с атомами материала резиста приводит к выбиванию вторичных электронов. При этом некоторые вторичные электроны вылетают за. пределы подложки и экспонируют резист (так называемый эффект близости). В результате экспонированная область оказывается значительно больше по размеру относительно диаметра, электронного пучка.

Функция поглощённой энергии (PSF) может быть определена экспериментально [1, 2] по профилю экспонированного участка. Но точное решение задачи поиска коэффициентов аппроксимации исходной функции возможно только для представления функции двумя гауссианами. Тогда как при попытке достичь большой точности аппроксимации, используя три или более гауссианы, коэффициенты аппроксимации однозначно не определяются.

Для более глубокого изучения процессов, лежащих в основе эффекта близости, используется метод математического моделирования. Такие исследования актуальны для анализа эффективности современных и перспективных методик улучшения разрешения электронно-лучевой литографии, так как позволяют быстро и не затратно получить необходимую информацию о поглощенной веществом энергии. Для расчетов потерь энергии электрона при прохождении через вещество существуют модели, как использующие представления о непрерывном характере зависимости потерь энергии от пройденного пути [3, 4], так и комбинированные дискретно-континуальные модели [5].

При учёте процессов рассеяния электронов на атомах вещества необходимо знать значение рассеивающего параметра в формуле Резерфорда. Существуют различные способы оценки этого параметра, в частности, широко применяются модели Моллера [6], Ингами [7], Бишопа [8] и Томаса-Ферми [9]. Отдельно моделируется процесс генерации вторичных электронов, для которого первостепенную роль играет способ определения энергии, затраченной первичным электроном. Для решения этой задачи широко применяются модели, описанные в работах Моллера [10], Гризински [11], Лильеквиста [12] и других [13].

В настоящей работе предлагается учитывать потери энергии электронов на возбуждение и ионизацию атомов комбинированным методом, основанным на моделях Бете и Моллера. Использование приближений модели Моллера позволяет избежать переоценки вклада энергии первичных электронов в образование вторичных. Эта модель применима для электронов с энергиями в диапазоне 1-100 кэВ, т.е. для так называемых электронов средней энергии (middle-energy electrons), для которых можно пренебречь влиянием релятивистских эффектов.

2.    Модель взаимодействия электронного луча с веществом

Процессы упругого и неупругого рассеяния электрона на атомах вещества носят случайный характер, а их вероятность определяется дифференциальными сечениями. Используя выражения для этих сечений, по методу Монте-Карло возможно рассчитать ряд траекторий электронов. Количество рассчитанных траекторий определяет статистическую достоверность практически необходимых усреднённых физических характеристик процесса, таких как, например, коэффициент обратного рассеяния, пространственное распределение плотности выделенной энергии.

Приведём постановку численного эксперимента. Здесь исследуемый образец представляет собой бесконечный слой монокристаллического кремния с постоянной решётки а = 5.43 А. Луч электронов представляется в виде конечного числа независимо рассматриваемых электронов, соответствующего дозе экспонирования. Моделирование движения первичного электрона начинается с точки на поверхности кремния. Начальные координаты на плоскости (ж, у, z = 0) для этой точки разыгрываются согласно распределению Гаусса для полярного радиуса то:

j'e-beam(тo) = — exp (--),

7Г«о     \ «о2/ где je-beam — плотность тока, 1о — полный ток электронного луча, «о — «эффективный» радиус пучка, и для произвольного полярного угла уо:

ж = т о cos уо,      у = то sin Уо.

Исходное направление движения электронов перпендикулярно плоскости поверхности (z — 0) кремния. Начальная энергия для всех электронов принимается одинаковой и соответствующей энергии электронного луча.

Рассматриваются следующие процессы взаимодействия электронов с веществом: упругое рассеяние на атомах кремния, приводящее к отклонению электронов от первоначального направления движения; возбуждение атомов, сопровождающееся малыми потерями энергии электрона; ионизационные столкновения с появлением вторичного электрона; радиационное торможение в кулоновском поле атомов. Для учёта всех этих процессов применяется комбинированная дискретно-континуальная модель, в рамках которой предполагается, что электрон теряет энергию как непрерывно на протяжении всего пути, так и скачкообразно (только при образовании вторичного электрона) в точках, соответствующих изменению направления движения.

Средняя длина пробега электрона без изменения направления движения Atot определяется из соотношения

^A tot

— ^C^Bethe + ^{n Ze} Single — ^tot —

^A Bethe     ^A Single

После того как разыграна длина свободного пробега электрона, разыгрывается тип рассеяния, с выбиванием вторичного электрона (Single) или без выбивания (Bethe), согласно вероятностям:

Atot pBethe — X , ABethe pSingle —

^A tot

^A Single

где c — дифференциальное сечение рассеяния, n — концентрация атомов. A — длина пробега электрона между рассеиваниями на атомах решетки, р — вероятность столкновения данного типа.

В точке рассеяния электрон изменяет направление своего движения. Полярный угол рассеяния электрона является случайной величиной с плотностью вероятности [14]:

I (Ө) — 0.613Z2/3 a0G2(y), где ао — радиус Бора. Здесь используются следующие обозначения:

у — O.885ka o Z ^1/3 sin(0.5Ө),

G(y) — у ¹ / y($)sm(2y$)d$, 0

<Дж) — e^- 0 . 6& r.

Дифференциальное сечение упругого рассеяния (случай Бете) рассчитывается по формуле Резерфорда:

'                            de _         Z 2 Е 4

dQ   4Е2(1 - cos Ө + 2^n)2 , где Q — телесный угол, Ө — угол рассеяния, An — рассеивающий параметр Нигами [15]:

me⁴^ 2 Z ^2/3

^Л—    2Һ 2 Е ■

Общие потери энергии электрона в зависимости от прейдённого пути S рассчитываются по формуле Бете:

1    1 \ dS / Bethe — 2В ^К^г ln1^, 1 г АЕ 2яе4 (1) е — "Е, в — —, mv2 где Е — кинетическая энергия первичного электрона, е — перенаппая энергия (АЕ). нормированная по Е, Z — зарядовое число атома, mv2 — кинетическая энергия первичного электрона, It — энергия ионизации степени г.

Первичный электрон при выбивании вторичного электрона испытывает скачкообразную потерю в энергии, соответствующей сумме энергии, затраченной на разрыв связи с начальной энергией вторичного электрона. Но так как после ударной ионизации вторичный электрон физически не отличим от первичного, за первичный принимается электрон с большей энергией. Соответственно энергия вторичного электрона не должна быть больше 0.5 от энергии первичного электрона перед столкновением. Распределение этой энергии определяется дифференциальным сечением для неупругого рассеяния, рассчитываемым по модели Моллера [5]. Для нерелятивистских электронов уравнение для дифференциального сечения выглядит следующим образом:

-

s(1 — s) )*

⁽ da ⁾      В ⁽ 1       1

\ ds /м    Exs²^ (1 — s)²

Для того чтобы дважды не учитывать потери энергии на ионизацию, формула (1) для непрерывной потери энергии электрона приводится к следующему виду:

( dE )    ( dE )       ( dE )

dS/ = V dS 7 Bethe ⁺ XdS ) Single ’

(dE)    = NZ /1/2 Es(£) ds.

V dS ) Single         J_£c        \ ds ) M

Так как электроны низкой энергии не оказывают значительного влияния на итоговые значения поглощенной энергии, за нижний предел интегрирования здесь выбирается некоторое отличное от нуля значение критической минимальной энергии, в настоящей работе определённое как sc = 11 /Emax = 1.63 • 10^-4. Это допущение позволяет значительно упростить расчёты.

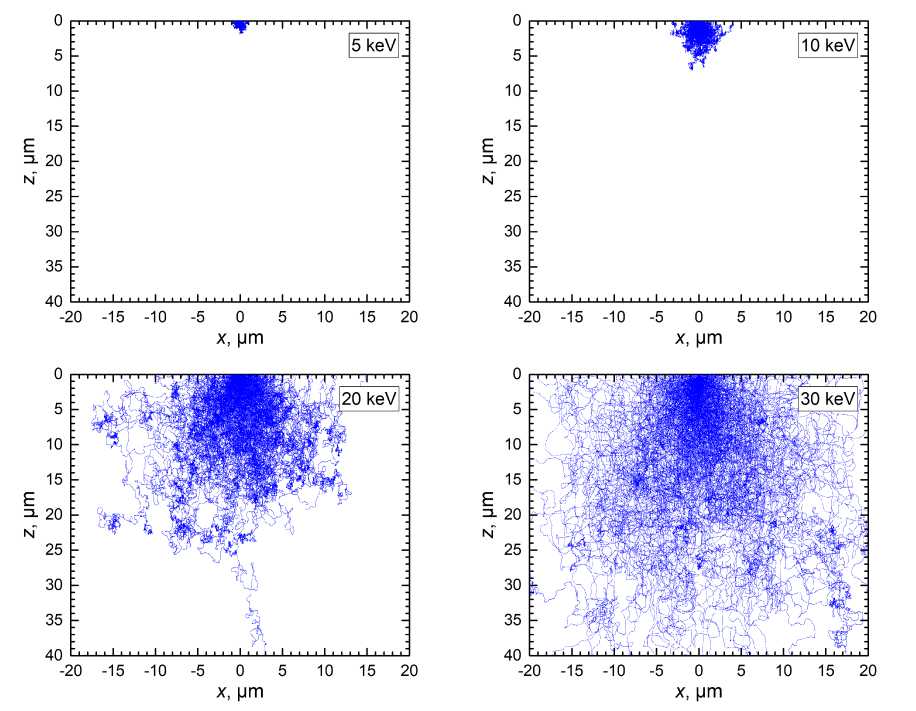
Рис. 1. Траектории электронов в монокристаллическом кремнии в проекции z-x Уу = 0) в зависимости от начальной энергии пучка: 10, 20, 30 и 40 кэВ. Количество электронов в пучке N = 300

Начальное значение энергии вторичного электрона E se определяется из следующего соотношения:

E se = E - E pe - h = [^Е Vd^E) dS,

0 \ dS ) Single где Epe — энергия первичного электрона после столкновения, ]Е А суммарный путь, пройденный первичным электроном без выбивания вторичного электрона. Согласно [16], вторичные электроны при образовании могут с равной вероятностью вылетать под любым углом относительно направления движения первичного электрона.

Рассмотрение движения электрона в среде прекращается, когда его энергия становится меньше энергии ионизации атома кремния hi. В этот момент рассматриваемый электрон становится неразличимым от электронов среды, а его энергия передаётся веществу.

3.    Результаты моделирования

Результаты расчетов случайных наборов траекторий электронов ( N = 300) в кремнии в зависимости от начальной энергии пучка представлены на рис. 1. Здесь показано качественное согласие результатов моделирования с наблюдаемым в экспериментах эффектом увелечения площади засветки поверхности с ростом энергии пучка. Вследствие этого, в промышленных литографах, в частности в многолучевом литографе MAPPER©, для увеличения конечного разрешения используются электронные пучки низких энергий. Но так как при снижении ускоряющего напряжения электронной пушки осложняется фокусировка луча, для работы с конкретной системой резист-подложка требуется предварительно подбирать оптимальные значения ускоряющего напряжения.

С ростом энергии пучка, кроме увеличения области засветки, также увеличивается и общая область распространения электронов пучка и выбиваемых ими вторичных электронов в толще вещества. На рис. 1 для энергий 20 и 30 кэВ хорошо различимы отдельные области повышенной концентрации электронов вдали от точки входа пучка в вещество. Их наличие объясняется поведением первичных электронов с относительно низкими энергиями, которые на небольших отрезках пути образуют множество вторичных электронов.

х, пт

б)

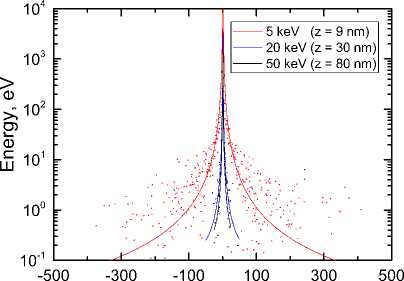
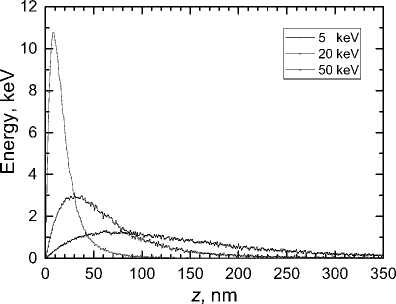
Рис. 2. Профиль поглощенной энергии в кремнии для начальной энергии пучка. 5 (красная кривая), 20 (синяя) и 50 кэВ (чёрная): а) распределение энергии по оси ж для фиксированного значения координаты у = 0 и для набор а координат z = 9. 30 и 80 им; б) распредслепие энергии по оси z на прямой ж = 0, у = 0. Количество электроиов в пучке N = 100 000

а)

Результаты расчёта характерных профилей поглощенной энергии в кремнии представлены на. рис. 2. Анализ полученных профилей показывает, что с увеличением энергии пучка область поглощенной энергии вытягивается вдоль направления хода пучка (по оси z) и сужается в перпендикулярной плоскости (ж-у). Наблюдаемое уширение области поглощенной энергии в плоскости ж-у называется ближним эффектом близости. Этот эффект связан с рассеянием первичных электронов в сторону поверхности. Для уменьшения влияния этого эффекта необходимо увеличивать энергию пучка. Но одновременно с этим увеличивается вероятность образования вторичных электронов, которые экспонируют резист в ещё большей области, на расстояниях порядка 10 мкм от места попадания пучка в вещество (дальний эффект близости).

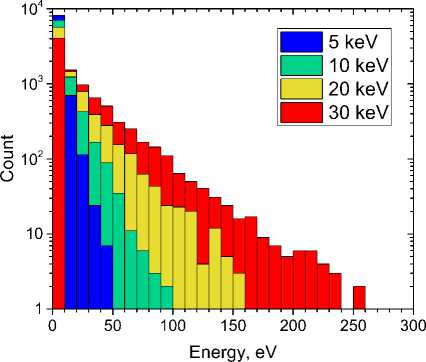
Рис. 3. Гистограммы для зависимости количества, вторичных электронов от их начальной энергии. Представлены гистограммы для пучков из N первичных электронов с начальными энергиями 5 (синие столбцы для N = 38 500), 10 (зелёные для N = 51700), 20 (жёлтые для N = 47 600) и 30 кэВ (красные для N = 8000)

Гистограмма распределения начальной энергии вторичных электронов в зависимости от начальной энергии электронов в падающем луче представлена на рис. 3. Для оценки характера, полученного распределения гистограмма, нормирована, на. количество вторичных электронов. Из полученного распределения следует, что меньшая энергия первичного пучка ведет в среднем к меньшей энергии вторичного электрона.

4.    Заключение

В работе была, предложена, дискретно-континуальная модель движения электронов в кристаллическом кремнии для оценки разрешающей способности электронно луча. Данная модель соответствует общефизическим представлениям о движении электронов в веществе и описывает основные зависимости для первичных и вторичных электронов в кремнии: профили поглощенной энергии, размеры областей распространения первичных и образования вторичных электронов, гистограмма, энергий образованных вторичных электронов. На основе предложенной модели проведено численное моделирование процесса, взаимодействия пучка, электронов с кремниевой подложкой для начальных энергий в диапазоне 5-50 кэВ. Расчеты, проведенные в настоящей работе, могут быть использованы для подбора, оптимальных значений ускоряющего напряжения электронно-лучевой литографии в системах с кремниевой подложкой.