Моделирование методом потоков течения в диффузорной части регулируемого сопла тормозного двигателя возвращаемого аппарата

Важным этапом возвращения космических аппаратов является посадка. Перспективные многоразовые космические возвращаемые аппараты капсульного типа с малым аэродинамическим качеством для обеспечения мягкой посадки используют посадочные двигательные установки с глубоким регулированием тяги [1]. Элементами конструкции таких двигателей могут быть регулируемые сопла. Режим работы таких сопел изменяется, как правило, путем несимметричного перекрытия части площади критического сечения сопла и изменения давления в камере сгорания, что, наряду с применением прямоугольного критического сечения, сильно усложняет картину течения в сопле. Эти особенности могут приводить к потере тяги, появлению дополнительных боковых сил и увеличению нестационарности течения, что необходимо учитывать при разработке системы. В работе [2] исследовалось влияние одностороннего изменения площади критического сечения при сохранении плоскости симметрии на характеристики течения в сопле с круглым поперечным сечением и кососрезанным выходным сечением. Обнаружено появление дополнительной неском-пенсированной нормальной силы.

В настоящей работе проводится численное исследование течений в соплах с косо-срезанным выходным сечением и прямоугольным критическим сечением при его несимметричном перекрытии на основе параллельных алгоритмов консервативного метода потоков с использованием модели вязкого теплопроводного газа.

Вычисления проведены в широком диапазоне изменения параметров, влияющих на характер и структуру потока внутри сопла, в частности, на отрыв потока внутри сопла. Такими параметрами являются отношение полного давления в конфузорной дозвуковой части сопла к полному давлению в окружающей среде и изменяемая площадь критического сечения сопла. Рассматривается влияние вышеуказанных параметров на положение отрыва потока, на поперечные силы, действующие на внутреннюю поверхность диффузорной части сопла. Приводятся поля газодинамических характеристик течения.

Постановка задачи. Численный метод

Рассматривается течение вязкого теплопроводного сжимаемого газа в диффузорной части сопла. Форма диффузорной части номинального сопла и связанная система координат OXYZ , используемые в расчетах, приведены на рис. 1.

Критическое сечение сопла имеет прямоугольную форму. Сразу за критическим сечением имеется небольшой участок сопла, в котором форма сечения постоянна и совпадает с формой критического сечения номинального сопла. Далее находится переходный участок, на котором форма сечения сопла меняется от прямоугольной до круглой. Далее диффузорная часть сопла состоит из состыкованных между собой участков, имеющих форму усеченных прямых конусов. В дальнейшем используются безразмерные единицы длины, в которых линейные размеры отнесены к величине радиуса окружности, описанной около прямоугольного критического сечения номинального сопла.

Центр принятой в работе правосторонней системы координат совпадает с центром критического сечения. Ось ОХ направлена вдоль оси сопла, ось ОY направлена вдоль большей стороны прямоугольника, образующего критическое сечение, а ось OZ — вдоль меньшей стороны критического сечения. Меридиональный угол θ отсчитывается в плоскости ОYZ от положительного направления оси OY в сторону положительного направления оси ОZ.

Размеры номинального критического сечения по осям ОУ и OZ составили 1 * = 1,557 и 1 * = 1,255, соответственно, а площадь критического сечения при этом равна s * = 1,954. Тринадцать угловых точек контура сопла определяют его геометрию. Угловые точки обозначены на рис. 1 точками и цифрами 1–13, а их координаты приведены в таблице.

Таблица

Координаты угловых точек, определяющих геометрию диффузорной части сопла

№ точки	x	y
1	0,000	–0,779
2	0,871	–0,779
3	1,938	–1,065
4	2,269	–1,228
5	4,131	–1,495
6	6,038	–1,762
7	7,944	–1,867
8	9,851	–1,967
9	11,758	–2,066
10	13,664	–2,167
11	15,571	–2,267
12	17,477	–2,367
13	19,079	–2,452

Плоскость среза сопла имеет вид Ax + By + D = 0, с коэффициентами, имеющими значения А = 0,318; В = 0,948; D = –3,733. Срез сопла расположен вдоль оси ОХ от значения х_{s 1} = 6,43 до значения х_{s 2} = 19,079. ^s

Кроме номинального сопла, описанного выше, рассматривались сопла, у которых при неизменной форме диффузорной части площадь критического сечения менялась, моделируя перекрытие критического сечения регулируемого сопла. Форма критического сечения оставалась прямоугольной, оно располагалось по оси y между значениями у = - 1_у */2 и у = 1 */2, по оси z между значениями z = z z и z = 1 */2 ( z_z — переменная z -координата края критического сечения). Переменная граница критического сечения изображена на рис. 1 пунктирной линией. Площадь критического сечения при этом равна s_z * = ( 1 */2 - z z ) 1 *.

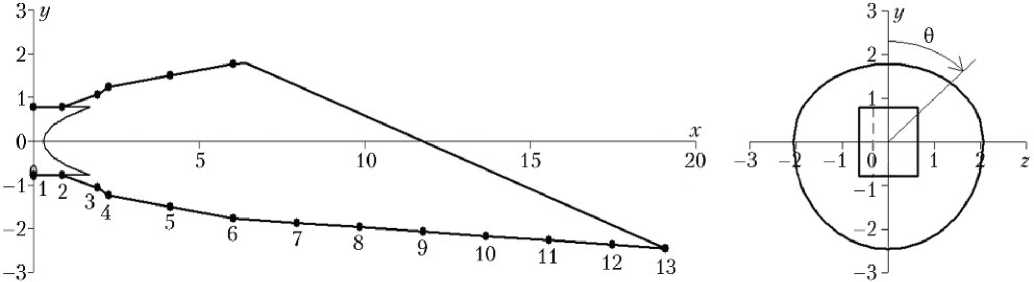
Рис. 1. Форма диффузорной части сопла: 1-13 — номера угловых точек контура сопла; 0 — меридиональный угол; — — — переменная граница критического сечения сопла

Примечание. Используются безразмерные переменные.

Отметим, что в случае номинального критического сечения рассматриваемая задача симметрична относительно плоскости OXY , и эта симметрия нарушается при изменении площади критического сечения.

Рассматриваемая среда — вязкий теплопроводный газ с отношением удельных теплоемкостей γ = 1,4.

Параметры газа в критическом сечении считаются заданными и постоянными. В дальнейшем используются безразмерные единицы, в которых плотность, скорость и температура отнесены к ρ*, V *, T * — плотности, скорости и температуре в критическом сечении. При таком выборе безразмерных единиц давление в критическом сечении р * = 1/γ = 0,714. Полное давление p ₀ = p *((γ + 1)/2)γ/(γ – 1) = 1,352.

Температура газа во внешней среде на бесконечности принималась равной Т_a = 0,135. Число Рейнольдса, вычисленное по параметрам и диаметру критического сечения, составляет Re = 2∙10⁶. В расчетах задавалось отношение полного давления адиабатически заторможенного потока к давлению внешней среды на бесконечности n = р ₀/ р_a .

Численные исследования осуществлялись на основе нестационарного варианта консервативного метода потоков [3, 4], основанного на конечно-разностной аппроксимации законов сохранения, записанных в интегральной форме для каждого конечного объема вычислительной сетки. Разработанные параллельные алгоритмы [5] реализованы на вычислительном комплексе кластерной архитектуры Межведомственного суперкомпьютерного центра Российской академии наук. В расчетах использовалось до 1 000 процессоров.

Расчетная область представляет собой цилиндр радиусом 25 и длиной 100 безразмерных единиц, расположенный вдоль оси ОХ от начала координат.

Вычисления проводились на вычислительных сетках, которые экспоненциально сгущались при приближении к стенкам сопла как внутри, так и снаружи сопла.

Используемые сетки обладают осевой симметрией, в которой ось симметрии совпадает с осью ОХ . Число разбиений сетки в расчетах достигало значений: 400 — по оси ОХ , 150 — по радиусу и 100 — по меридиональному углу θ. На рис. 2 для примера показан фрагмент вычислительной сетки в сечении x = const на переходном участке сопла.

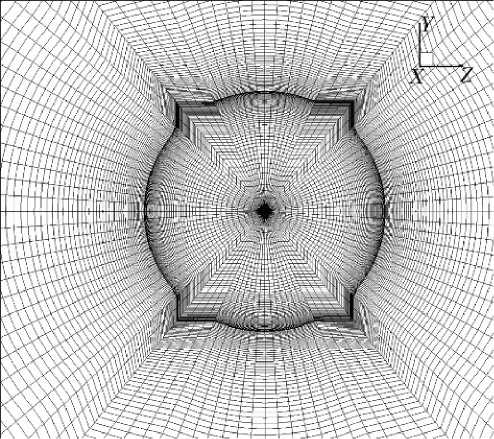
Рис. 2. Фрагмент сетки на переходном участке сопла

Результаты расчетов

В настоящем разделе приводятся результаты расчетов течения в сопле для значений параметра n = 80; 60; 40; 20 и относительной площади критического сечения сопла s* = ^s */ ^s о , изменяемой в интервале 1,0...0,5.

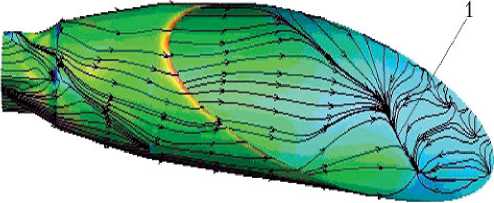
Особенностью получившихся численных решений является наличие отрыва потока на внутренней поверхности сопла. Для значений n = 80; 60; 40 линия первоначального отрыва находится в пределах среза сопла между значениями х = х_{s 1} и х = х_{s 2}. Для n = 20 линии первоначального отрыва находятся между критическим сечением и плоскостью х = х_{s 1}. На рис. 3 в качестве примера показаны линии тока, а цветом — значения V_t -проекций касательных скоростей на меридиональные плоскости скоростей в ближайших к внутренней поверхности сопла расчетных точках при от н осительной площади критического сечения = 0,8 для значений n = 80; 60; 40; 20. На рисунке хорошо видна первоначальная линия отрыва потока, которая сдвигается вглубь сопла при уменьшении n .

На рис. 4 показана зависимость координаты точки отрыва x_s на поверхности сопла от числа n для меридионального угла θ = π и отно с ительной площади критического сечения =1; 0,9; 0,8; 0,5.

Как и следовало ожидать, точка отрыва x_s сдвигается к критическому сечению при уменьшении n и .

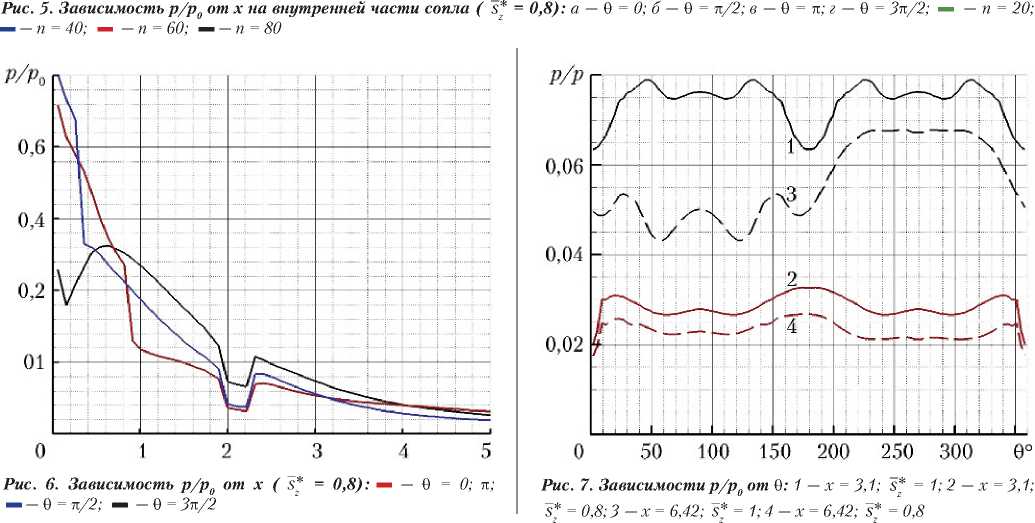
На рис. 5 показаны распределения отношения давлений р / р ₀ на внутренней поверхности сопла вдоль линий с постоянными значениями меридионального угла θ = 0; π/2; π; 3π/2 для о т носительной площади критического сечения = 0,8.

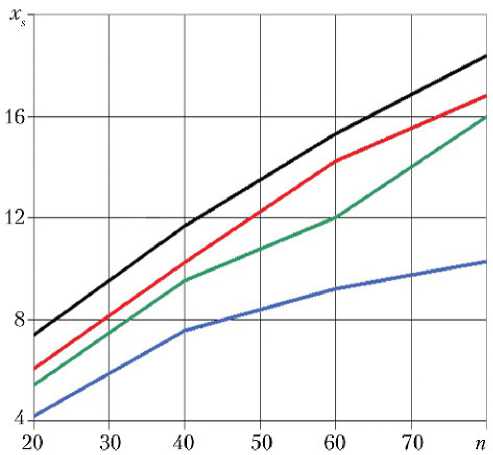
Рис. 4. Зависимость координаты точки отрыва x_s от n на поверхности сопла в меридиональной плоскости 0 = п :

— —   = 1; — —   = 0,9; — —   = 0,8; — —   = 0,5

Примечание. — относительная площадь критического сечения.

а)

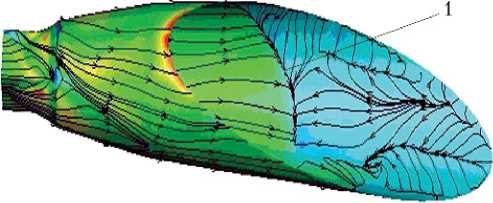
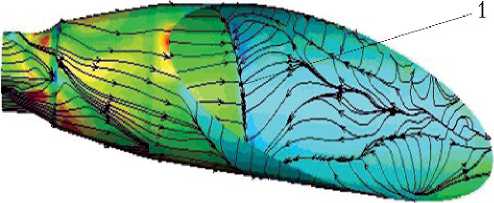
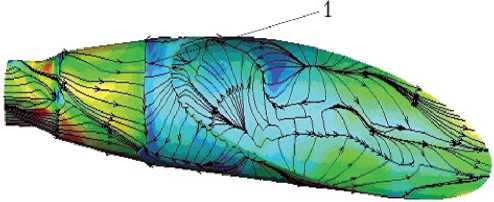
Рис. 3. Линии тока и значения скоростей в ближайших к поверхности сопла расчетных точках: а — n = 80; б — n = 60; в — n = 40; г — n = 20; 1 — линия отрыва

Примечание. V_t – значение проекции касательной составляющей скорости на меридиональную плоскость; n = р ₀ / р_a — отношение полного давления газа на входе в сопло к давлению внешней среды на бесконечности; относительная площадь критического сечения = 0,8. Масштаб в поперечных координатах увеличен.

в)

г)

Распределения давлений при n = 80; 60; 40; 20 совпадают до точек отрыва потока или до края сопла и далее принимают значения, близкие к атмосферному давлению, а точка отрыва потока смещается к критическому сечению при уменьшении n .

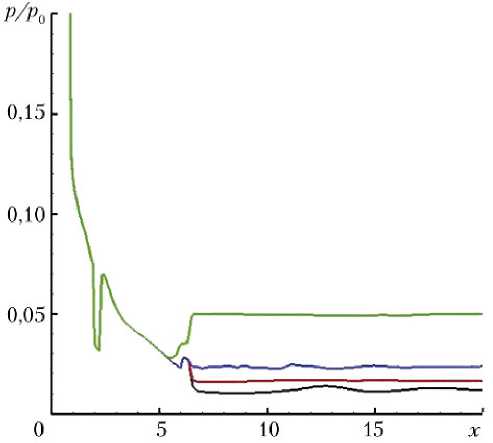
На рис. 6 для = 0,8 представлены зависимости р / р ₀ от х на стенке сопла в той его части, где для рассмотренных значений n еще нет отрыва потока. В этом случае результаты расчетов практически не зависят от n (с точностью до толщин линий на рис. 6). Приведены кривые, полученные в сечениях θ = 0; π/2; π; 3π/2. Данные в сечениях θ = 0; π практически совпадают и изображены одной кривой.

Видно, что в случае θ = 3π/2 сразу за критическим сечением образуется зона разрежения, которая при увеличении х сменяется зоной повышенного давления. Эта зона повышенного давления хорошо видна на рис. 7, где показаны зависимости р / р ₀ от азимутального угла θ в двух сечениях х = 3,1; 6,42 и для двух значений относительной площади критического сечения = 1; 0,8.

Возникающая несимметричность (относительно θ = π) зависимости р/р ₀ от θ в сечении х = 3,1 сглаживается по мере приближения к выходному сечению сопла. Отметим, что на рис. 7 кривые 1, 2 описывают зависимости для n = 80; 60; 40; 20, в то время как кривые 3, 4 описывают зависимости для n = 80; 60; 40, так как в случае n = 20 отрыв потока происходит до сечения х = 6,42.

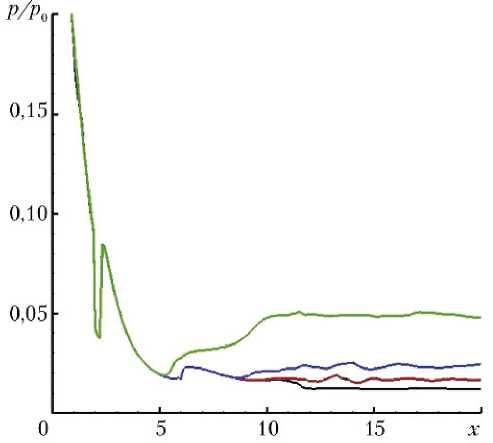
а)                                                       б)

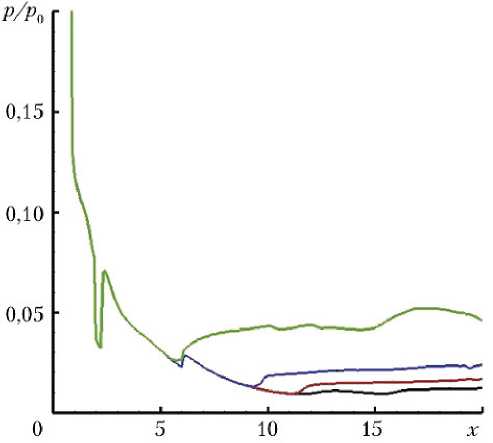
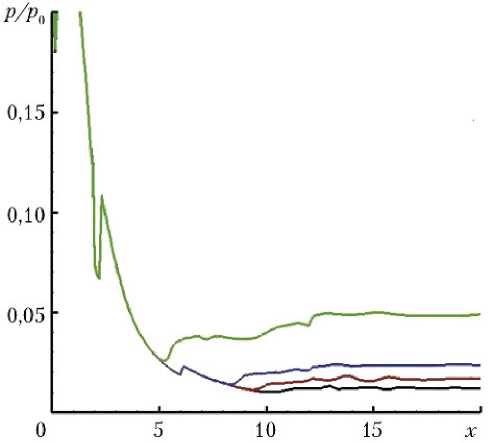
в)                                                                 г)

На рис. 8 показаны зависимости нормальной относительной силы = ( F_y–F_ay )/ I * от относительной площади критического сечения для значений n = 80; 60; 40.

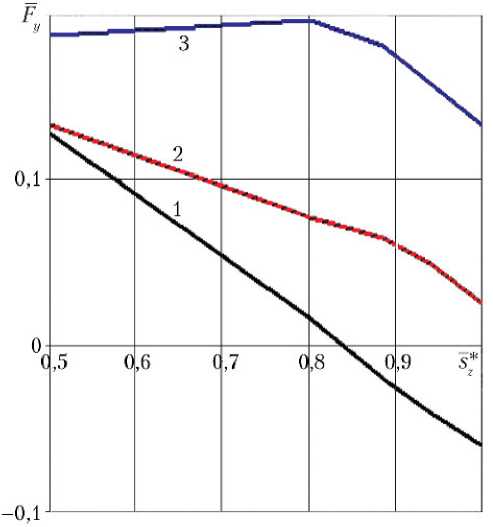
Рис. 8. Зависимость относительной силы от относи-

У тельной площади критического сечения : 1 — n = 80;

2 — n = 60; 3 — n = 40

Здесь — проекция на ось ОY газодинамических сил, действующих на внутреннюю боковую поверхность диффузорной части сопла; _a — y -составляющая газодинамической силы, действующей на внутреннюю диффузорную часть сопла, если считать, что давление внутри сопла постоянно и равно атмосферному p_a ; I *= ρ* V *² s_z * — импульс потока в критическом сечении. Положительные значения говорят о том, что струя вытекает из сопла отклоненной вниз, в сторону отрицательных значений у , и наоборот — отрицательные значения говорят об отклонении струи вверх, в сторону положительных значений у . Чем больше абсолютное значение | |, тем на больший угол отклоняется струя.

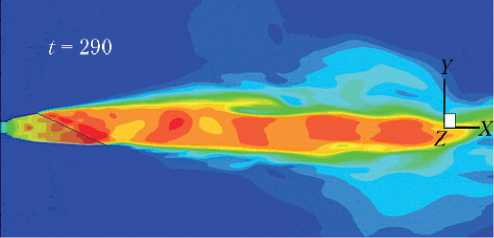
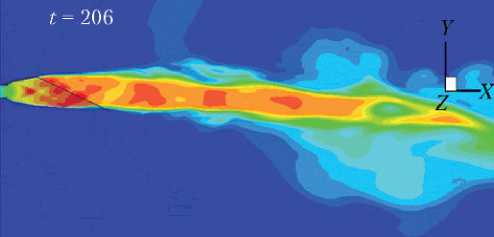
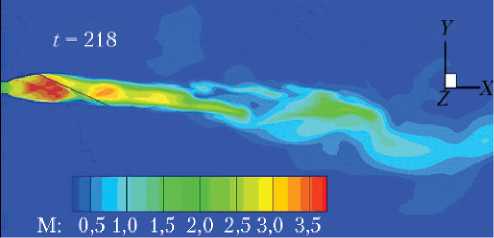
Иллюстрацией этого является рис. 9, на котором показаны поля чисел Маха в плоскости ОХY в случае n = 60 и значений = 1,0; 0,8; 0,5.

В соответствии с кривой на рис. 8 струя на рис. 9 незначительно отклоняется вниз при = 1, и с уменьшением это отклонение увеличивается.

На рис. 10 показаны зависимости коэффициента силы = F_z / I * от относительной площади критического сечения для значений n = 80; 60; 40; 20.

а)

б)

в)

Рис. 9. Поле локальных чисел Маха в плоскости OXY (n = 60): а —   = 1; б —   = 0,8; в —   = 0,5

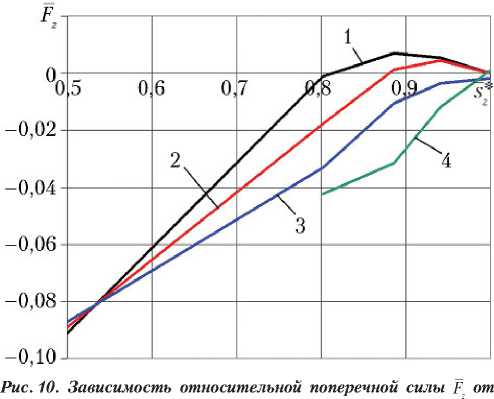
относительной площади критического сечения : 1 — n = 80;

2 — n = 60; 3 — n = 40; 4 — n = 20

• — проекция на ось ОZ поперечных газодинамических сил, действующих на внутреннюю боковую поверхность диффузорной части сопла. Положительные значения кривой говорят о том, что струя вытекает

из сопла отклоненной в сторону отрицательных значений z , и наоборот — отрицательные значения говорят об отклонении струи в сторону положительных значений z . Отметим, что значения по порядку величины значительно меньше, чем значения сил на рис. 8, и отклонение струи вдоль оси ОZ менее заметно, чем вдоль оси ОY .

а)

б)

в)

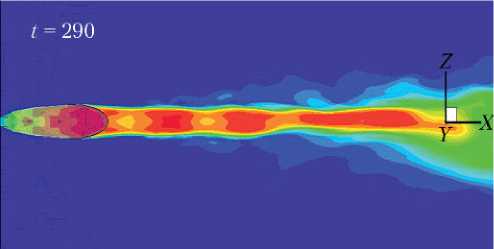
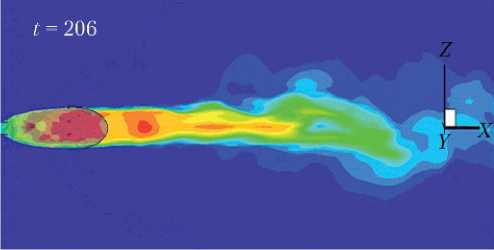
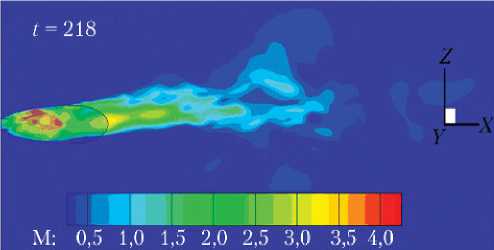
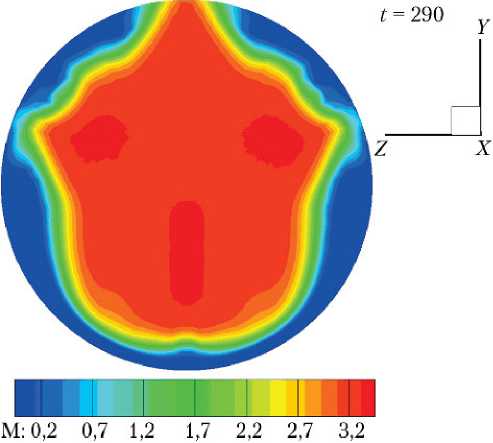
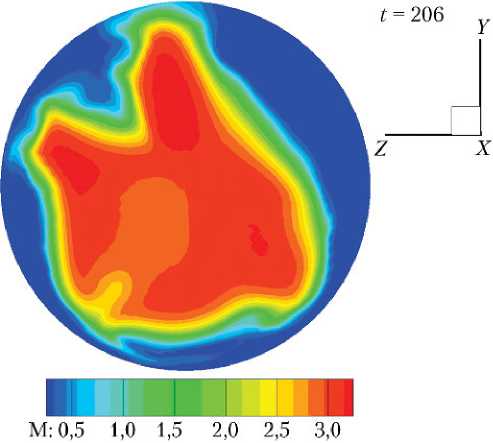
Рис. 11. Поле локальных чисел Маха в плоскости OXZ

а)

б)

(n = 60): а —   = 1; б —   = 0,8; в —   = 0,5

На рис. 11 показаны поля чисел Маха в плоскости ОХZ для n = 60 и значений = 1,0; 0,8; 0,5.

На этом рисунке отклонений струи в какую бы то ни было сторону не заметно при значениях = 1,0; 0,8. И только при = 0,5 струя заметно отклоняется в сторону положительных значений z , что находится в соответствии с поведением кривых на рис. 10.

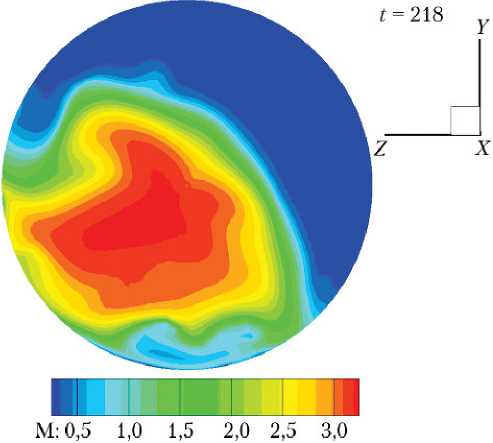
На рис. 12 показаны поля чисел Маха в плоскости х = x_{s 2}, проходящей через дальний край среза сопла для n = 60 и трех значений = 1,0; 0,8; 0,5.

в)

Рис. 12. Поля локальных чисел Маха в плоскости х

x s2

(n = 60): а —   = 1; б —   = 0,8; в —    = 0,5

Видно, что при уменьшении s* струя отклоняется вниз и в сторону отрицательных значений z .

Заключение

Проведены систематические расчеты течения воздуха в сверхзвуковом сопле сложного профиля с кососрезанным выходным сечением и прямоугольным критическим сечением при вариации отношения полного давления к давлению в окружающем пространстве и площади критического сечения.

Расчеты показали, что в рассмотренном диапазоне изменения параметров течения в сопле реализуется отрывное течение в зоне длинной образующей сопла, при этом образуется нормальная сила в плоскости симметрии сопла. Величина и направление этой силы зависят от нерасчетности истечения, вызванной как отношением давлений, так и изменением площади критического сечения.

Изменение площади прямоугольного критического сечения со смещением его центра относительно оси симметрии сопла приводит к образованию поперечной силы, перпендикулярной плоскости симметрии.