Моделирование многослойных углеродных нанотрубок

В последние годы в физике конденсированного состояния все более популярными становятся объекты нанометрового масштаба. Особый интерес проявляется к углеродным наноматериалам как из наиболее перспективным для применения в различных областях промышленности. К одной наиболее интересных полиморфных модификаций углерода относятся нанотрубки. Выделяют одно- и многослойные нанотрубки, среди которых, в свою очередь, также выделяются несколько подвидов [4], [8].

Модельно процесс формирования однослойной нанотрубки можно представить как сворачивание плоской графеновой сетки вокруг некоторого выбранного кристаллографического направления [3], [7], [8]. Данное направление сворачивания определяется так называемыми индексами хиральности ( n , m ), характеризующими вектор хиральности (сворачивания) C_h (рис. 1). Индексы хиральности [3], [7], [12] определяют количество элементарных трансляций вдоль двух направлений гексагональной графитовой сетки с параметром ячейки a = 2,46 Å (рис. 1).

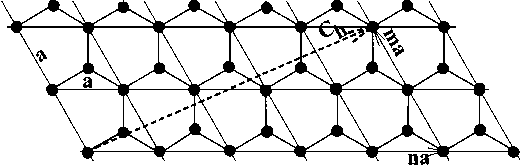
Рис. 1. Сворачивание графитовой сетки (1 слой) вдоль вектора Ch

Набор индексов хиральности ( n , m ) должен удовлетворять следующим условиям [3]:

n > 0, m > 0, n > 2m.(1)

Длина вектора хиральности определяет радиус формируемой нанотрубки [3], [7]:

Ch a П. 2"_

R =   = — nn — nm + m .(2)

П П

Кроме радиуса индексы хиральности также определяют так называемый трансляционный вектор, характеризующий минимальный шаг по длине нанотрубки (то есть вдоль ее оси) [3], [7]:

т   3a ^a Г^-     Z 2"         _m

T =------ nn — nm + m ,         (3)

2 n * d_R

R где dR = НОД(2n – m, 2m – n).

В качестве характеристики нанотрубки дополнительно вводят такой параметр, как степень хиральности [2]:

^m k =     .

Степень хиральности k меняется в пределах от 0 (нанотрубки типа «зиг-заг») до 0,5 (нанотрубки типа «кресло»). Эти два типа нанотрубок считаются прямыми (или ахиральными). Все остальные нанотрубки – хиральные, степень хиральности лежит в пределах 0 < k < 0,5 [2], [3], [7].

Таким образом, индексы хиральности полностью определяют геометрические размеры формируемой нанотрубки – минимальные радиус и длину. Для получения нанотрубок той же степени хиральности, но большего радиуса следует использовать соответствующие индексы, кратные минимальным. Для получения нанотрубок большей длины необходимо использовать длину, равную целому числу трансляционных векторов.

После определения геометрических характеристик нанотрубки рассчитываются все остальные параметры моделирования и находятся координаты всех атомов, образующих нанотрубку [3].

Многослойная нанотрубка состоит из нескольких определенным образом расположенных слоев. Наиболее часто многослойные нанотрубки подразделяются на 2 вида: типа «русская матрешка» и типа «свиток» (рис. 2) [2], [4], [8], [10], [13].

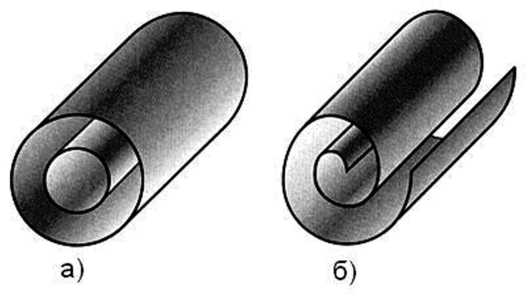
Рис. 2. Типы многослойных нанотрубок: а) «русская матрешка»; б) «свиток»

Иногда можно встретить описание многослойных нанотрубок, образованных в виде «шестигранных призм» [5]. В основании таких трубок лежит правильный шестиугольник. Таким образом, углы между любыми двумя смежными гранями равны по 120°. Но такие структуры встречаются крайне редко.

Многослойная нанотрубка типа «русская матрешка» – это структура, представляющая собой набор соосно расположенных однослойных нанотрубок на определенном расстоянии друг от друга. Каждая такая трубка определяется собственными индексами хиральности ( n, m ). Однако в данном случае радиусы слоев должны быть такими, чтобы межслоевое расстояние также находилось в допустимых для углеродных материалов пределах (3,354–3,600 Å). Средним для многослойных нанотрубок при этом считается расстояние, равное 3,444 Å [2], [13]. Таким образом, одна из главных задач при моделировании многослойных нанотрубок типа «русская матрешка» – это определение индексов хиральности всех «слоев» – однослойных нанотрубок, образующих данную структуру. На основании полученных индексов и заданной длины возможно моделирование каждого слоя в отдельности, аналогично моделированию однослойных нанотрубок [3], [7].

При формировании многослойных нанотрубок типа «русская матрешка» следует учитывать тот факт, что слои могут иметь как одинаковую степень хиральности, так и различную [2]. Поэтому общая хиральность многослойной нанотрубки определяется не так однозначно, как в случае однослойных нанотрубок. В случае же различной хиральности слоев следует учитывать, что величина трансляционного вектора для каждого слоя также будет различной [3], поэтому для такой трубки нельзя четко задать определенную длину.

Для начала рассмотрим случай, когда многослойная нанотрубка образована из слоев одинаковой степени хиральности. В данном случае степень хиральности многослойной нанотрубки будет такой же, как и хиральность отдельных однослойных нанотрубок, ее образующих. Поэтому величина межслоевого расстояния будет одинаковой в пределах многослойной нанотрубки определенной хиральности [2], [9].

С учетом (2) и (4) после преобразований можно прийти к следующему выражению для радиуса однослойной нанотрубки [2]:

R — a— n 1 - k + k² . (5) 2 n

Таким образом, межслоевое расстояние между двумя однослойными нанотрубками с одинаковой степенью хиральности k можно выразить следующим образом [2]:

d n — R-) — R — — V1 — k + k ( n_? — n .) —

R 2       1                                    2       1

2 n                         (6)

= a- V1 — k + k 2 *(nmm f) , 2n где n1, n2 – индексы n двух соседних трубок, nmin – минимальный индекс n для нанотрубок данной степени хиральности k, f – параметр, определяющий число периодических трансляций вдоль направления, задаваемого индексами (n, m) между двумя соседними нанотрубками (f = 1, 2, 3, …) [2].

Поскольку межслоевое расстояние – это величина, лежащая в некоторых пределах [2], [13], из всего множества индексов хиральности необходимо подобрать только те, для которых это условие будет выполняться. Путем компьютерного перебора [2] всевозможных индексов хиральности: n в диапазоне от 1 до 10 000 ( m , соответственно, в диапазоне от 0 до 5000 для соответствующих n ) было выявлено, что лишь 5 степеней хиральности дают требуемый результат (см. таблицу).

Степени хиральности, для которых возможно формирование многослойных нанотрубок одинаковой хиральности

n (min)	m (min)	k = m/n	f	dR , Ǻ
1	0	0,0	9	3,5237
5	1	0,2	2	3,5884
10	3	0,3	1	3,4799
5	2	0,4	2	3,4132
2	1	0,5	5	3,3907

Таким образом, исходя из заданных индексов хиральности внутреннего слоя на основании вышеприведенных рассуждений возможен расчет индексов хиральности всех слоев формируемой многослойной нанотрубки. Для этого производится:

• 1.    Ввод индексов хиральности ( n , m ) внутреннего слоя;

• 2.    Расчет степени хиральности по (4);

• 3.    Расчет внутреннего радиуса нанотрубки по (2) или (5);

• 4.    Расчет n_min для нанотрубок данной хиральности и определение параметра f согласно таблице;

• 5.    Ввод количества слоев и расчет межслоевого расстояния по (6);

• 6.    Последовательный расчет радиусов всех слоев на основании информации о радиусе предыдущего рассчитанного слоя и величины межслоевого расстояния;

• 7.    Исходя из радиусов слоев и степени хиральности – расчет соответствующих индексов n и m каждого слоя;

• 8.    Расчет трансляционного вектора по (3) и всей длины нанотрубки;

• 9.    Расчет координат атомов во всех слоях аналогично расчету однослойных нанотрубок [3].

В связи с одинаковой степенью хиральности как «исходных» трубок, образующих отдельные слои, так и итоговой многослойной величина трансляционных векторов и, соответственно, длина всех слоев будет одинаковой.

В случае, когда каждая нанотрубка, образующая отдельный слой, имеет свою степень хиральности, нельзя судить об итоговой хиральности получаемой таким образом многослойной нанотрубки. В данном случае указывается хиральность трубки, образующей внутренний слой. Далее путем перебора индексов ( n , m ) определяется хиральность каждого следующего слоя при условии того, что межслоевое расстояние должно лежать в указанных ранее пределах. Для этого производится перебор индексов хиральности: индекс n меняется начиная от индекса n предыдущего слоя; m – от нуля до n/2 (согласно условиям (1)). По причине того, что индекс n в большей степени отвечает за радиус нанотрубки, изменение n ограничено радиусом внешнего слоя (максимальным радиусом многослойной нанотрубки), который можно приблизительно оценить исходя из внутреннего радиуса трубки, максимально допустимого межслоевого расстояния и числа слоев.

В том случае, когда условие по межслоевому расстоянию выполняется для нескольких нанотрубок (с различными степенями хиральности), выбирается та, для которой величина межслоевого расстояния оказывается минимальной, попадающей в данный интервал, то есть наиболее близкой к межслоевому расстоянию в графите (3,354 Å) [2], [13]. Таким образом, индексы хиральности каждого следующего слоя рассчитываются исходя из индексов хиральнос- ти предыдущего. Очевидно, что в данном случае межслоевое расстояние не будет величиной постоянной: оно будет меняться от слоя к слою в зависимости от индексов хиральности соседних слоев [2], [9].

Как отмечалось ранее, в зависимости от индексов хиральности величина трансляционного вектора для разных слоев также будет различной (рис. 3). И может возникнуть ситуация, когда при заданной длине нанотрубки один слой будет иметь длину, намного превышающую заданную по причине большого значения трансляционного вектора (рис. 3).

Рис. 3. Различная длина слоев разной хиральности

В данном случае вначале рассчитываются величины трансляционных векторов всех слоев. Далее длина нанотрубки подбирается в соответствии со следующими условиями.

• 1.    Выбранная длина должна быть как можно ближе к требуемой. Если это невозможно, то в качестве длины выбирается величина самого большого трансляционного вектора.

• 2.    Длины всех слоев должны быть примерно одинаковыми. В случае более коротких слоев используется некоторое целое число трансляционных векторов. Тогда получаемая модель будет наиболее адекватной.

Последовательность действий при формировании моделей многослойных нанотрубок с различной степенью хиральности слоев будет следующей:

• 1.    Ввод индексов хиральности ( n , m ) и расчет радиуса внутреннего слоя;

• 2.    Ввод количества слоев и расчет максимально возможного радиуса внешнего слоя;

• 3.    Путем перебора индексов ( n , m ) расчет всевозможных радиусов следующего слоя;

• 4.    Из полученных радиусов (и соответствующих им индексов) выбор тех, которые:

• а)    дают межслоевое расстояние, попадающее в требуемые границы [2], [13];

• б)    дают наименьшее межслоевое расстояние;

• 5.    Получение индексов всех слоев аналогично п. 3–4;

• 6.    Задание предполагаемой длины нанотрубки;

• 7.    Расчет значений векторов трансляций всех слоев;

• 8.    Расчет длин всех слоев, соответствующих заданной длине;

• 9.    Выбор векторов трансляции для каждого слоя и пересчет длины согласно приведенным ранее требованиям;

• 10.    Расчет координат атомов во всех слоях аналогично расчету однослойных нанотрубок [3]. После того как определены индексы хиральности каждого слоя и выбрана длина формируемой нанотрубки, производится расчет координат атомов в каждом слое аналогично расчету отдельных однослойных нанотрубок.

При формировании нанотрубок типа «свиток» (рис. 2б) производится сворачивание одного графенового листа вокруг некоторого кристаллографического направления с непрерывным увеличением радиуса [10]. Таким образом, имеется некий внутренний радиус (начало свитка) и внешний. Нанотрубка при этом остается незамкнутой. Радиусы витков не могут быть абсолютно произвольными – они подчиняются тем же правилам, которые действуют для однослойных нанотрубок [3], [7], и также определяются индексами хиральности. К тому же межслоевое расстояние (между любыми двумя соседними витками) должно находиться в допустимых для углеродных материалов пределах [2], [13]. Поэтому должен иметься четкий механизм, согласно которому при построении каждого витка производилось бы плавное увеличение радиуса. Таким образом, при моделировании нанотрубок типа «свиток», при сворачивании графенового листа для расчета координат каждого следующего атома необходим пересчет радиуса (приращение на некоторую величину) [9], [11]. Так как межслоевое расстояние должно быть постоянным (для обеспечения плавности переходов от витка к витку), существует ограниченное число нанотрубок типа «свиток», которые могут быть построены. Это ограничение накладывается условием, что все витки, если бы их взяли по отдельности, должны иметь одинаковую степень хиральности. То есть возникает ситуация, схожая со случаем формирования многослойной нанотрубки типа «русская матрешка» со слоями одинаковой хиральности. Таким образом, возможно лишь 5 видов нанотрубок типа «свиток» (см. таблицу).

Более того, моделирование хиральных нанотрубок с переменным радиусом – задача далеко не тривиальная. Поэтому в данной работе произведено моделирование лишь «идеальных» (или ахиральных) нанотрубок типа «свиток».

Для иллюстрации того, что нанотрубки типа «свиток» и «русская матрешка» возможно отличить друг от друга, были смоделированы следующие многослойные нанотрубки:

• •    нанотрубка «русская матрешка» типа «зигзаг»; внутренний слой имеет индексы хиральности (9, 0), что соответствует радиусу ~3,5 Å,

число слоев равно 3, все слои имеют одинаковую хиральность, длина трубки ~20 Å;

• •    нанотрубка «свиток» типа «зиг-заг», внутренний виток имеет радиус ~3,5 Å, число витков равно 3, расстояние между витками ~3,35 Å, длина трубки ~20 Å.

Далее были рассчитаны теоретические дифракционные картины рассеяния от полученных моделей в FeKα излучении и в качестве наиболее контрастной для сравнения выбрана s-взвешенная интерференционная функция H(S) [1], [3], [6]. Результат сравнения полученных картин рассеяния от выбранных моделей нанотрубок (рис. 4) показал: положения пиков интенсивности в дан- ных моделях находятся примерно в одинаковых пределах величины дифракционного вектора [1], [6], но характер данных пиков отличается.

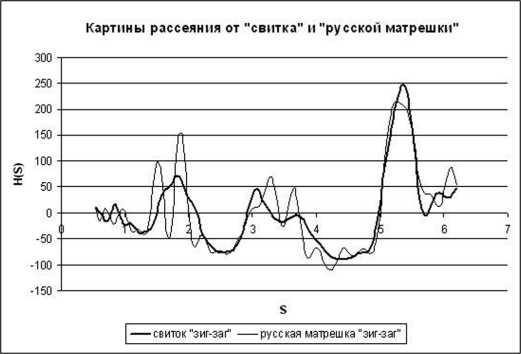
Рис. 4. Картины рассеяния от нанотрубок типа «свиток» и «русская матрешка»

На рис. 4 видно, что пики интенсивности рассеяния «русской матрешкой» более четкие, менее размытые, сформированы при определенных положениях модуля дифракционного вектора, в отличие от «свитка».

При моделировании многослойных нанотрубок типа «русская матрешка» других конфигураций с большим числом слоев картины рассеяния сохраняли характер в расположении пиков интенсивности, однако сами пики возрастали по величине и становились еще более четкими. Моделирование многослойных трубок «русская матрешка» других конфигураций (по длине, радиусу, числу слоев) и сопоставимых им нанотрубок типа «свиток» и сравнение картин рассеяния от полученных моделей дает аналогичный результат. Необходимо учитывать, что в нанотрубках типа «свиток» происходит постоянное увеличение радиуса при формировании каждого витка, соответственно, каждый такой виток имеет как внутренний радиус, так и внешний. При этом:

• •    внутренний радиус отличается от внешнего на величину межслоевого расстояния;

• •    внутренний радиус очередного витка равен внешнему предыдущего.

Таким образом, при построении многослойных нанотрубок типа «русская матрешка» и «свиток» с одинаковыми внешним и внутренним радиусами получается, что «свиток» будет иметь меньшее количество слоев. На рис. 5 видно, что нанотрубки «свиток» и «русская матрешка» имеют одинаковые внутренний и внешний радиусы. Однако у «свитка» всего 2 витка, а «русская матрешка» образована тремя слоями.

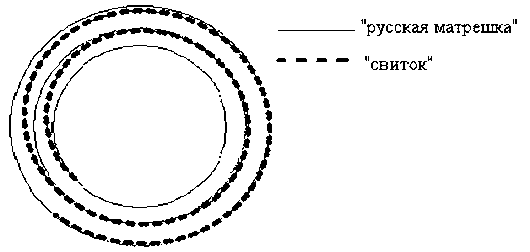
Рис. 5. Многослойные нанотрубки «свиток» и «русская матрешка» с одинаковыми внешним и внутренним радиусами

Соответственно, нанотрубка типа «свиток» из трех витков в результате будет иметь больший внешний радиус, чем трехслойная нанотрубка типа «русская матрешка». Также число атомов в данных моделях у «свитка» будет несколько большим. Это необходимо учитывать при моделировании и сравнении многослойных нанотрубок данных типов.

ВЫВОДЫ

В данной работе разработана методика и построен алгоритм формирования моделей, расчета координат атомов в многослойных углеродных нанотрубках типа «русская матрешка» различных конфигураций. Показаны ограничения, накладываемые на формируемые модели, связанные с геометрией и характеристиками нанотрубок, в связи с чем невозможно построить абсолютно произвольные многослойные трубки. Также разработан алгоритм формирования многослойных ахиральных («зиг-заг» и «кресло») нанотрубок типа «свиток» различных конфигураций.

Моделирование нанотрубок различных типов («русская матрешка» и «свиток») и последующий анализ теоретических дифракционных картин рассеяния, рассчитанных от полученных моделей, показали, что существует возможность (на основе рентгенографического эксперимента) идентификации нанотрубок, присутствующих в исследуемом образце.

Исследования проведены при поддержке Федеральной целевой программы «Научные и научно-педагогические кадры инновационной России» на 2009–2013 годы № П801 от 24 мая 2010 года.