Моделирование мультисервисной сети Центробанка РФ

Бахарева Н.Ф., Коннов А.Л.

В статье рассмотрена математическая модель неоднородного трафика одной мультисервисной сети. На основе этой модели с использованием методов уравнений баланса потоков в сети и двумерной диффузионной аппроксимации процессов функционирования СМО, а также системы моделирования GPSS World, получены основные показатели производительности сети.

Постановка задачи

С 2006 г. Центробанк РФ перешел на технологию коллективной обработки платежной информации (основной обрабатывающий центр для половины регионов России размещается в Санкт-Петербурге). При этом трафик существенно зависит от вида участника расчетов (учреждение Банка России (БР), клиент БР, участник электронного обмена) и типа платежа (внутри региональный электронный, межрегиональный электронный, почтовый). Так внутри региональный платеж РКЦ проходит (весьма укрупненно) следующие этапы: ввод, предварительная обработка в РКЦ, передача в РЦИ, предварительная обработка в РЦИ, передача в Санкт-Петербург, обработка, передача в РЦИ, обработка в РЦИ, передача в РКЦ - получатель, обработка в РКЦ и выдача. Каждый из этапов сопровождается обменом электронными служебными документами. Кроме того, существуют технологические операции: открытие/ закрытие счетов, модификации программного обеспечения, обновление нормативно-справочной информации и др. Среднее время осуществления такого платежа 20 мин.

Посылка формируется в РКЦ (у клиента) на этапе предварительной обработки. В посылке может быть как один, так и несколько тысяч документов. Время обработки в ЦОИ несопоставимо мало (мс) относительно суммарного времени предварительных обработок и транспорта информации. Для конечного пользователя среднее время обработки его документа составляет 20 мин. Трафик существенно зависит от вида отчета (их около 200). Среднее время формирования отчета (с учетом технологии параллельной обработки) составляет 10 мин.

Требуется промоделировать многопроцессорный сервер обработки данных с целью определе- ния его загрузки в зависимости от интенсивности входного потока, а также оптимального количества процессоров. Для проверки точности предложенной методики, на которой построена программная система PROBMOD, проведены также расчеты по программе GPSS World.

Решение задачи

Для решения поставленной задачи авторами использована методика приведения неоднородного потока заявок к однородному потоку так называемых «обобщенных» заявок и метод двумерной диффузионной аппроксимации процессов функционирования систем массового обслуживания (СМО). Для этого рассматриваются два типа трафика. Это в первую очередь платежи, где приходит порядка 45-50 тыс. документов в сутки (док/С). Получаем интенсивность поступления запросов первого типа трафика, равную X ^{( 1 )} = 0,5787 док/С, то есть через интервалы времени 1,728 С поступают заявки первого типа. Примем трудоемкость обслуживающего устройства за единицу. Интенсивность обработки платежа получим, исходя из времени его обработки – мС (среднее значение порядка 500 мС), то есть ц ⁽¹⁾ = 1/(0,500) = 2 док/С.

Второй тип трафика – это поток статистической отчетности. Всего существует 127 форм отчетности. При этом ежедневно поступают порядка 60 форм, причем примерно половина от кредитных организаций, а половина от расчетно-кассовых центров. Таким образом, имеем 7620 документов в сутки. Тогда интенсивность запросов второго типа X ^{( 2 )} = 0,088 док/С , то есть очередной отчет поступает через интервал времени в 11,3386 С. Интенсивность обработки запросов получим, исходя из времени обработки в мС (среднее значение порядка 450 мС), то есть ц ⁽²⁾ = 1/(0,45)=2,22 док/С.

Методика приведения неоднородного трафика к обобщенному состоит в следующем. Используем бесприоритетную дисциплину обслуживания FCFS (первым пришел – первым обслужен). Под неоднородностью трафика будем подразумевать многомерностьпотоказаявок и различиемаршру-тов движения для каждого типа заявок. Пусть от внешнего источника S0 в сеть (на вход i-ой СМО) поступает многомерный поток заявок с интенсивностями X0m) и дисперсиями D0m) для каждого типа заявок m (m = 1, 2 ... M; i = 1, 2 ... n). Рассмотрим случай, когда сетевая модель системы характеризуется одной общей матрицей вероятностей передач заявок для всех типов P={Pij} (i ;j = 1; 2 … n). Составим уравнения баланса интенсивностей потоков заявок для каждого типа m на входе и выходе каждой СМО сети.

n

^ i^{m )} = х om ⁾ + z p^ m'.       (1)

-i

Решением систем линейных алгебраических уравнений (1) определяем интенсивности потоков типа m на входе и выходе каждой СМО сети X(m). Так как коэффициент загрузки системы Si потоком типа m будет составлять р(m) = X(m)/р(m), где р(m) - интенсивность обслуживания заявки типа m в системе Si , то суммарная загрузка системы Si со стороны всех M потоков будет равна р Е = ^р (m) . Тогда условие существования стационарного режима представится в виде ρiΣ <1 (i = 1, 2 … n) и коэффициент простоя системы Si равен qi =1-ρiΣ .

Параметры потоков заявок из множества за-

т о ⁶ = (X ⁽¹⁾ /ц ⁽¹⁾ )/X ^об + (X ⁽²⁾ /ц ⁽²⁾ )/X ^об =

= (0,5787/2)/0,6667 + (0,088/2,22)/0,6667 =

=0,4934 С.

Используя выражения (2) и (3), получим, что коэффициент загрузки i-ой СМО потоком обобщен-об ных заявок ρi составит

„ об об —об       ( m ) ( m )

Р i = X i •^тLi /Рi = P i s ,       (4)

а в нашем случае pоб = xоб .тоб = 0,6667-0,4934=0,3289.

С другой стороны р=X(1) /р(1) + X(2) /р(2) = 0,3289 .

Следовательно, однородный поток обобщенных заявок создает ту же нагрузку, что и неоднородный поток.

Тогда уравнения баланса интенсивностей однородного потока и дисперсий времени между соседними обобщенными заявками на входе и выходе каждой СМО сети можно записать

n хоб = хоб+2pjAj,         (5)

j = 1

M где XОб = 2 XО”) .

m=1

Уравнения равновесия длядисперсийбудут иметь вид

явок типа m усредним с целью приведения неоднородного потока к однородному. Эти параметры будут описывать так называемую «обобщенную» заявку. При этом должно соблюдаться условие, чтобы однородный поток заявок на обслуживание обобщенной заявки создавал такую же нагрузку на каждую СМО сети, как и неоднородный поток. Поэтому параметры потока обобщенных заявок определим посредством усреднения параметров потока типа m по интенсивностям поступления X ^{( m )} . Тогда интенсивность поступления потока обобщенных заявок на вход i -ой СМО

M

X об = Z X ( ^{m )} ,                (2)

m= 1

об вх

+ ∑ ^⎜

об 3

X^^

⎜ об ⎟

V ^X i J

об

^X j p ji

∑ _⎜ ^⎜

V X об J

( x (m ) ) ³

⎜ об ⎟

V ^X 0 i J

( m )

^D 0 i

+

. (6)

—(D.™ j p ji

+

1 - p ji

(X об ) ² p ji

)

В выражении (6) значения выходных дисперсий D _в ^о _ы ^б _{х j} будут определяться по методу двумерной диффузионной аппроксимации [1], но дисперсия времени обслуживания обобщенной заявки будет равна

а для нашей задачи х об = X(1) + X(2) =0,5787+0,088=0,6667 док/С, а среднее время обслуживания обобщенной заяв ки

M тоб = 5»im)/ц !” )/х Г,       (3)

* = 1

где р ^{( m )} = 1/т^ ) ( i = 1, 2 ... n ).

Для нашей задачи это время равно

nF          ( m )                      ( m )

D ^об = У D^(m) ^ i +(т^(т)-т^оН ^ i

Dμi =∑⎢ Dμi   об + τμi τμi об ⎥ , j=1⎢⎣         λi                          λi ⎥⎦ где T^mm) и D^”) - среднее и дисперсия времени обслуживания заявки типа m в i-ой СМО.

В нашем случае маршруты движения в сети для заявок из разных потоков различны и описываются матрицами вероятностей передач P ^{( m} )= { p j ) } , в формуле (1) вместо значений p ji

( m )

нужно брать p j_i , а в формулах (5) и (6) вмес-

об M (m) ^(m)             .

то pji – значения p = ∑ p       обобщенной m=1     λоб матрицы вероятностей передач, что следует из условия нормировки в матрице вероятностей передач для потока обобщенных заявок.

При вышеприведенных исходных данных с помощью программной системы GPSS получаем загрузку обслуживающего устройства, равную 0,289. В то время как, при помощи программной системы PROBMOD, разработанной авторами, получаем результат 0,290 (см. результаты на рис.1-2).

START TIME	END TIME	ELOCKS	FACILITIES	STORAGES
0 . DOO	86400.000	9	1	0

MAME	VALUE
CHAN	10001.000
QCHAN	10000.000

LABEL	LOC	BLOCK TYPE	ENTRY COUNT CURRENT COUNT RETRY
	1	GENERATE	49999	0	0
	2	QUEUE	49999	0	0
	3	SEIZE	49999	0	0
	4	DEPART	49999	0	0
	5	ADVANCE	49999	0	0
	6	RELEASE	49999	0	0
	7	TERMINATE	49999	0	0
	Ei	GENERATE	1	0	0
	9	TERMINATE	1	0	0

FACILITY	ENTRIES	UTIL .	AVE .	TIME AVAIL.	OWNER	PEND	INTER	RETRY	DELAY
CHAN	49999	0.2 89		0.500  1	0	0	0	0	0

QUEUE	MAX CONT.	ENTRY ENTRY(0)	AVE.CONT.	AVE.TIME	AVE.(-0)	RETRY
QCHAN	1     0	49999  49999	0.000	0.000	0.000	0

Рис. 1 . Результаты моделирования в программной системе GPSS World

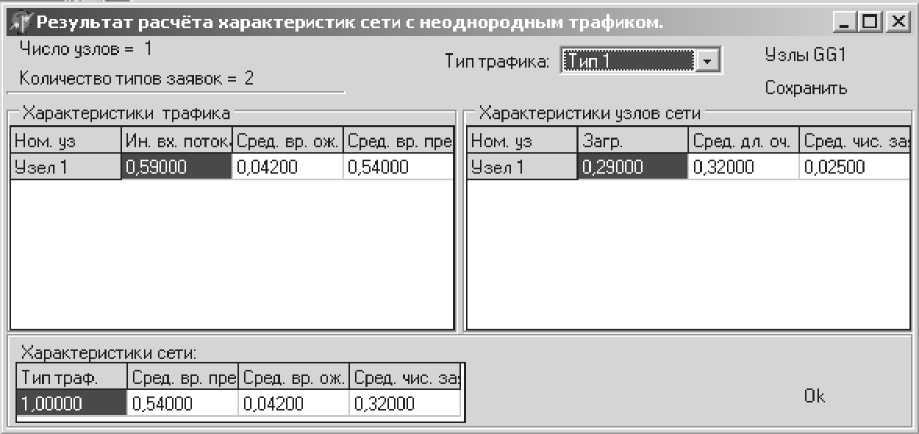
Рис. 2. Результаты моделирования в программной системе PROBMOD

При помощи пакета GPSS получаем загрузку обслуживающего устройства равную 0,04. При помощи программной системы PROBMOD получаем точно такой же результат.

Полученные результаты, а именно загрузка обслуживающего устройства, говорят о том, что при имеющихся интенсивностях поступления заявок на обработку (0,289 + 0,04) устройство загружено на 33% (см. рис. 1-2, таблицу 1). В реальных системах такая загрузка является хорошим показателем, так как в этом случае имеем 67% запас производительности.

Таблица 1. Результаты моделирования для 2-го типа трафика (1 вариант)

Программная система	Интенсивность вх. потока λ док/с	Загрузка ρ
PROBMOD	0,088	0,04
GPSS World	0,088	0,04

Рассчитаем интенсивность входного потока таким образом, чтобы загрузка устройства была на уровне 70%. Из формулы (4) имеем:

λiоб =ρiоб/τμобi =0,7/0,4934=1,418 док/С.

Откуда получим интенсивности входных пото-ковзаявок: X ⁽¹⁾ = 1,228 док/Си X ⁽²⁾ = 0,187 док/С. Проверим полученные результаты при помощи систем моделирования (см. таблицу 2).

Таблица 2. Результаты моделирования для 1-го типа трафика

Программная система	Интенсивность вх. потока λ док/с	Загрузка ρ
PROBMOD	1,20	0,610
GPSS World	1,20	0,614

Для второго типа трафика получаем следующие результаты (см. таблицу 3).

Таблица 3. Результаты моделирования для 2-го типа трафика (2 вариант)

Программная система	Интенсивность вх. потока λ док/с	Загрузка ρ
PROBMOD	0,19	0,085
GPSS World	0,19	0,084

Рассчитаем среднее время обслуживания обобщенной заявки для новых интенсивностей поступления заявок.

т об = (X(1)/ц(1) )/Х об + (X(2)/ц(2) )/Х об =

=(1,228/2)/1,418+(0,187/2,22)/1,418=0,492 С.

роб = хоб • Тоб =1,418-0,492=0,697 .

Таким образом, получаем требуемую загрузку обслуживающего устройства – 70%.

Примечание. Загрузка обслуживающего устройства рассчитана для случая, когда интервалы времени между поступлением заявок распределены по равномерному закону. Аналогично распределены интервалы времени между обслуживанием заявок.

Теперь проведем расчеты загрузки устройства в предположении пуассоновского входного потока с тем же средним интервалом 1,728 С. Время обработки заявки распределено по экспоненциальному закону со средним интервалом 0,5 С. При помощи пакета GPSS получаем значение за- грузки обслуживающего устройства равное 0,291 для первого типа трафика.

Рассчитаем загрузку устройства для второго типа трафика для случая, когда на входе имеем пуассоновский поток со средним интервалом 11,339 С. Время обработки заявки распределено по экспоненциальному закону со средним интервалом 0,45 С.

При помощи пакета GPSS получаем значение обслуживающего устройства равное 0,04 для второго типа трафика.

Полученные результаты внедрены и используются в Отделе информатизации ЦБ РФ по Оренбургской области.

Выводы

• 1.    Данные результаты получены для пяти обрабатывающих процессоров и интенсивности обработки поступающих запросов порядка мс. Такое количество процессоров обеспечивает загрузку обрабатывающего сервера на 33% при вышеуказанной интенсивности входного трафика. Таким образом, остается приличный запас ресурсов сервера для увеличения интенсивности входного трафика.

• 2.    Количество процессоров сервера зависит от поступающей нагрузки и поэтому может динамически меняться согласно проведенным расчетам. Такой подход позволяет прогнозировать и выбирать оптимальное число процессоров многопроцессорного сервера.

• 3.    Аналогичным образом можно решить задачу определения оптимального количества рабочих станций, необходимых для обработки поступающего потока заявок, при условии, что каждая рабочая станция располагает одним процессором.

• 4.    Законы распределений входного трафика и времени обслуживания при моделировании почти не влияют на такую характеристику как загрузка, но влияют на другие характеристики: среднее время ожидания, среднюю длину очереди и т.д.