Моделирование нагрева системы «покрытие подложка» при плазменной порошковой наплавке Stellite 190 сканирующей дугой

эффективный радиус пучка принимался R эфф =1,4 R c =1,4 мм. Были реализованы модели неподвижного источника и со сканированием пучка и движением детали. Расчеты проводились в пакете Mathcad 14.

В расчетах плотность и теплоемкость наплавляемого слоя считали аддитивными величинами с учетом процентного содержания компонентов в смеси, а теплопроводность приближенно оценивалась из соотношения [1].

m pi покр            i i=1                 (1)

где m – число компонентов в наплавляемом материале; A I - теплопроводность отдельного элемента; p i – относительная объемная концентрация элемента.

Теплофизические свойства элементов наплавляемого материала и матрицы взяты при температуре 1850 К. При данной температуре плавятся почти все компоненты Stellite 190 (см. табл. 1) кроме вольфрама. Однако растворение хрома и вольфрама в кобальте приводит к образованию эвтектика с температурой плавления 1573-1810 К [5]. Рассчитанные значения теплофизических свойств наплавляемого материала и подложки приведены в табл. 2, 3. Общая толщина наплавленного покрытия разбивалась на промежуточные слои равной толщины, каждый из которых наносится за промежуток времени t n . Рассматривая покрытие и подложку как единое целое, состоящее из заготовки и слоев, наносимых за время t n , для теплофизических расчетов можно воспользоваться понятием эквивалентной теплопроводности для многослойной системы [1].

Таблица 1. Химический состав и процентное содержание компонентов Stellite190

Состав Stellite 190	Co	Ni	Fe	C	Cr	Mn	Si	W
содержание, %	основа	1	2,5	3,3	26	0,5	1	14
Т пл . К	1765	1728	1811	субл.	2150	1518	1688	3693
Т кип . К	3230	3073	3145		2946	2353	3573	5933

Таблица 2. Теплофизические свойства покрытия Stellite 190

Т пл , К	λ, Вт/м∙К	С , Дж/кг∙К	ρ, кг/м3*103	а , м2/с*10-6
1573-1810	72,4	687	8,82	12

Таблица 3. Теплофизические свойства стали 19ХГНМА

Т пл , К	Т кип, С	λ, Вт/ м∙К	С , Дж/ кг∙К	ρ, кг/м3∙103	а , м2/с∙10-6
1813	3142	35	780	7,4	6,01

X

экв

n

Zai i=1

n

Z ^X i = 1 ^X i

hподл + n • gn hподл        gn

--+ n •-------X . X подл          покр

где n - число слоев, Д - толщина отдельного i -го слоя, а X — его теплопроводность. В нашем случае первый слой – это толщина h подл подложки , а наплавленный слой состоит из n слоев толщиной g n . За время наплавки одного слоя матрица прогреется на толщину h nodn = V ⁴ • a подл" tn . Эквивалентные теплоемкость и плотность нашей многослойной системы определяются по формулам:

В данном случае масса подслоя определяется через его плотность и объем:

V пок р = S кр g ( t )= πR эфф ² g ( t ), где g ( t ) – толщина наплавляемого слоя, зависящая от времени. За время наплавки одного подслоя масса прогретой зоны матрицы определяется через ее плотность (сталь 19ХГНМА) и объем прогретого материала ^ подл = ^П ^ фф • -j ⁴ • ^а подл • t . Тогда температуропроводность системы «по^кР^{ытие-по}д^ложка»      ^а экв = Л _Эк_в /⁽ С ^ • Р экв )

.

Пренебрегая потерями порошка при наплавке, толщина наплавленного слоя определяется как:

g (t ) =

G

порошка

t

т с +т . с . покр покр подл подл

;               (3)

^-покр ^{+ -}подл

5 кр Р

покр

^-покр Р 'покр ^{+ —}подл ' подл

Р экв = —-— ---------; (4)

^—покр ^{+ -}подл

где G порошка – массовый расход порошка; t – время воздействия, р _покр - плотность наплавляемого покрытия.

где ^- покр , ^С покр , ' покр масса, теплоемкость и плотность наплавленного подслоя покрытия.

Расчеты температуры при моделировании проводились по формуле [2]:

_T(,„_zl\-^Pi ' ^Ё\ ¹ exn ^{( Х + v}«-t ) 2 ^+[ y — A • sin t ® ' ⁽ t- - t ^{) ]] 2} T ^{( Х} , ^y , z ’ t - ) = 4 П5 Н J T Z t ; exp I                4 • a • ( t + 1 0 )

to

1 + 2 •Z cos i=1

f ^iz) IH )

• exp

-

V

n г

•

at

H ²

H

Ý 0

^i^d^ dt + To

H ^{5      0}

(6),

где P_Э= η⋅ P – эффективная мощность плазменной дуги; η = η ₁∙ η ₂, η ₁ – эффективный к.п.д. дуги, который в большинстве случаев можно принять равным 60%, η 2=0,7; H – толщина плоского слоя; t n – время нагрева, равное времени нанесения одного слоя покрытия; v_дв – скорость движения заготовки; ω =2 π /T_скан – частота сканирования дуги; T скан – период сканирования; амплитуда сканирования A = D /2; D – размах колебаний; t ₀ = R _эфф J 4 ⋅ a ; T 0 – начальная температура; q 1 ( ζ ) – функция интенсивности источника теплоты по толщине.

Будем считать, что источник нагрева поверхностный и согласно [3] для такого источника интеграл под суммой равен PЭ. При этом мощность дуги определяется через ток и напряжение дуги PД=IДUД; UД=С+0,03IД, где С=22 В для дуги прямой полярности. Кроме того, при температурах выше 2500 К следует учитывать потери за счет теплового переизлу-чения. Это можно учесть введением коэффициента К. Как показали расчеты его можно принять равным 0,8-0,9. Если же учесть протекание возможных экзотермических реакций в зоне наплавки при синтезе соединений, то он может принимать значения 1,0-1,1. Плоский слой H в (6) включает глубину прогрева подложки и толщину нанесенного слоя покрытия за время tn H = 4⋅a⋅tn +g(tn). Для сравнения процессов нагрева ниже приведены результаты расчетов неподвижной и сканирующей плазменной дугой.

Модель неподвижного источника нагрева. Пусть толщина покрытия 3 мм. Тогда из (5) при расходе порошка 8 г/мин время наплавки таким источником составит 1,5 с. Разобьем покрытие на равные слои и зададим время наплавки одного слоя. Считая, что слои равномерно накладываются друг на друга, примем толщину одного слоя равной «монослою», состоящему из частиц наплавляемого порошка одного диаметра 50 мкм. Тогда число слоев равно 60, а время наплавки одного слоя – t mm =0,01 с. Таким образом, толщина покрытия является дискретной величиной и зависит от времени наплавки одного слоя и количества слоев. Время воздействия в этом случае t n =t mm ⋅ n , где n – число нанесенных слоев. В нашем случае t n меняется от нуля до 1,5 с.

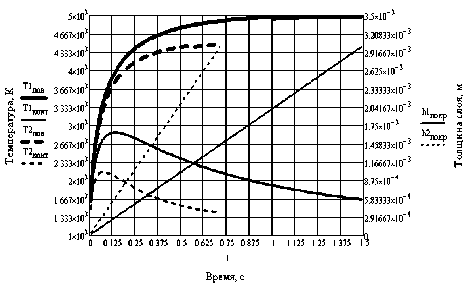
Рис. 1. Изменение температуры наплавляемого Stellite 190 и зоны контакта с подложкой при наплавке неподвижной дугой с I Д = 80А

На основе выражения (6) в Mathcad 14 была составлена программа, учитывающая рост плоского слоя H от времени t n , а также изменение эквивалентных теплофизических свойств системы «покрытие-подложка» после нанесения каждого слоя. Частота сканирования и скорость движения были равны нулю. На рис. 1 представлено изменение во времени температуры поверхности и на границе наплавляемого слоя с подложкой. Данные представлены с учетом роста толщины покрытия. Сплошные линии соответствуют расходу порошка 8 г/мин, а пунктирные линии – расходу 16 г/мин.

Из рис. 1 видно, что при расходе порошка 8 г/мин максимальная температура на поверхности заготовки равна 2880 К. При Т пл =1811 К расчетная глубина проплавления составила 0,8 мм при допустимом значении этой величины для наплавки на стали 0,1-0,3 мм. Повышение расхода порошка до 16 г/мин приводит к снижению температуры на границе с подложкой до 2160 К. Однако на поверхности практически через 0,1 с в обоих случаях температура становится выше температуры кипения основных компонентов материала наплавки (см. табл. 1) и дальнейший анализ процесса теряет смысл. Поэтому требуется включение режима с движением детали или сканированием пучка.

Модель источника со сканированием пучка. В этом режиме наплавки процесс нагрева в значительной степени определяется скоростью сканирования vскан и диаметром дуги. Вместе со скоростью движения детали vдв эти величины определяют время воздействия, период сканирования и коэффициент перекрытия, определяемые как tв=2Rэфф./νскан; Тскан=2D/νскан; КП=1–(νдвТскан/2Rэфф). Для данного режима также была составлена программа, учитывающая периодический рост покрытия в заданной области и изменение теплофизических свойств системы «покрытие-подложка» после нанесения каждого слоя и позволяющая определить глубину проплавления подложки. В расчетах менялся ток дуги, скорость движения детали и расход порошка при частоте сканирования 1,55 Гц (скорость сканирования 28 мм/с и размах колебаний 6 мм). Результаты расчетов представлены на рис. 2 и в табл. 4. Предполагалось, что рост покрытия начинается, когда на подложке достигается температура плавления. При токе дуги 80 А и скорости движения заготовки 2 мм/с плавление подложки начинается через 0.2 с, после чего начинается рост покрытия (рис. 2).

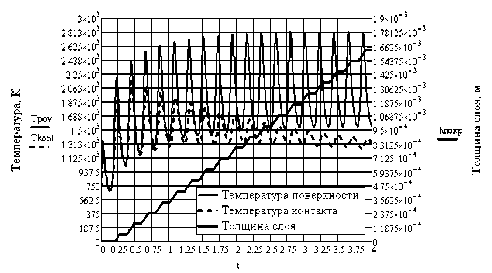
Время, с

Рис. 2. Изменение температуры наплавляемого Stellite 190 и зоны контакта с подложкой при наплавке сканирующей дугой: IД= 80 А, расход порошка 16 г/мин, частота сканирования 2,3 Гц, скорость движения 2 мм/с.

Введение сканирования дуги значительно меняет картину нагрева. Толщина покрытия увеличивается ступенчато – рост происходит за время воздействия дуги t в и затем прямая выходит на полку – плазменная дуга выходит за пределы заданной области. Процесс повторяется через каждые полпериода сканирования. Видно, что при токе дуги 80 А режим наплавки со сканированием становится оптимальным – при этом на поверхности для всех компонентов (кроме хрома) температура не достигает температуры кипения, а проплавление подложки происходит на допустимую глубину 0,15 мм. Максимальная глубина проплавления подложки рассчитывалась в момент достижения в зоне контакта с покрытием максимальной температуры. В таблице представлены результаты расчетов в зависимости от тока дуги, расхода порошка и скорости движения заготовки.

Таблица 4. Влияние тока дуги на глубину проплавления подложки

Расход порошка, г/мин	Ток дуги, А	S S § о R СР R с о к св я to	Скорость движения, мм/с
			2	4	6
16	60		-	-	0,091
	70		0,027	0,099	0,19
	80		0,15	0,19	0,29
	90		0,23	0,28	0,37
	100		0,32	0,36	0,46
	110		0,42	0,44	0,54
	120		0,50	0,52	0,62
32	60		-	-	0,024
	70		-	-	0,12
	80		-	0,054	0,21
	90		-	0,15	0,29
	100		0,078	0,24	0,37
	110		0,16	0,33	0,44
	120		0,23	0,41	0,52

Увеличение проплавления подложки с ростом скорости движения обусловлено снижением коэффициента перекрытия при сканировании и, следовательно, толщины наносимого слоя. Ранее проведенные эксперименты по наплавке Stellite 190 [6] при токах дуги 80-100А и расходе порошка 16 г/мин показали удовлетворительное качество наплавки и глубина проплавления заготовки составляла 0,10,3 мм, что вполне согласуется с данными в табл. 4.

Выводы:

• 1.    Предложено рассматривать процесс наплавки как нагрев многослойной системы с введением эквивалентных теплофизических свойств для системы «покрытие-подложка».

• 2.    В среде Mathcad 14 составлены программа для моделирования нагрева системы «покрытие-подложка» неподвижной и сканирующей дугой, позволяющая рассчитывать изменения температуры поверхности, зоны проплавления подложки, глубину проплавления подложки с учетом роста толщины покрытия.

  
  

  жимы наплавки.

  
  

• 3.    На основе моделирования показано 3. влияние тока и частоты сканирования плазменной дуги, скорости движения детали, расхода порошка на глубину проплавления подложки.

• 4.    Приведенные результаты моделирования позволяют определять оптимальные ре-    ^4.