Моделирование нагруженности лесохозяйственной машины в условиях нераскорчеванных вырубок

Основными препятствиями, затрудняющими работу лесокультурных агрегатов на вырубках, являются пни при количестве более 500 шт./га на избыточно увлажненных и более 600 шт./га на свежих и сухих почвах. В таежной зоне вырубки с количеством пней от 600 шт./га занимают свыше 55 % лесокультурного фонда, в том числе на Северо-Западе их более 80 % [1]. Кроме пней, помехи работе агрегатов создают порубочные остатки, валежник, оставленные растущие деревья, камни и корни [2].

Применение лесокультурных агрегатов сельскохозяйственного типа на вырубках в таежной зоне оказалось неэффективным вследствие отказов из-за поломок сошников, а также по показателям качества работы при встрече их с препятствиями в процессе непрерывного рабочего хода в почве [2].

Удаление препятствий (корчевка пней и проч.) в разы удорожает работы и ухудшает условия для развития леса, поэтому для условий таежной зоны оказалось целесообразным отказаться от непрерывного хода рабочих органов в пользу дискретной подготовки посадочных мест под лесные культуры. Работы в этом на

правлении были начаты в Ленинградской Лесотехнической академии под руководством профессора С. Ф. Орлова, наилучший эффект был получен при использовании динамических лун-кообразователей (ЛТУ–1, Л–2У и др.) [3].

Теоретическое обоснование проектных параметров для опытных образцов и опытных партий динамических лункообразователей типа Л–2У выполнено в работах профессора А. М. Цыпука [3 и др.], однако до настоящего времени не уделялось достаточного внимания вопросам нагружен-ности основных элементов этой машины (рычагов, опорных лыж).

При переходе от испытаний к производственной эксплуатации имели место непредвиденные поломки машин при взаимодействии с препятствиями (удары о камни, пни) на вырубках, что затрудняет внедрение лункообразователей в производство [4].

Кроме того, создание универсальной машины для лесовосстановления (рис. 1) на основе динамического лункообразователя типа Л–2У (для подготовки посадочных мест, посева и содействия естественному лесовозобновлению)

потребовало не только обоснования параметров высевающего приспособления, работоспособного в условиях нераскорчеванных вырубок, но также анализа нагруженности этого приспособления при встрече с препятствиями [4, 5].

В процессе работы такой универсальной машины для лесовосстановления в среде препятствий на вырубке возможны следующие неблагоприятные ситуации: удар рабочего органа (рычага) о пень, удар рычага о камень, удар опорной лыжи о пень, удар лыжи о камень после преодоления пня (т. е. падение с высоты пня), соударение опорно-приводного колеса высевающего приспособления с неподвижным препятствием (пнем), падение колеса с высоты пня и удар о камень. Во всех случаях должна обеспечиваться прочность узлов машины.

Следует заметить, что до настоящего времени теория работы лесохозяйственных машин в среде препятствий на вырубках в режиме разнообразных ударов разработана недостаточно, особенно для условий таежной зоны [2, 6].

а

б

Рис. 1. Универсальная машина на базе лункообразователя [9] а – подготовка посадочных мест; б – посев семян

Трудности в разработке теории имеют математическую и физическую природу. Математические трудности возникают при учете геометрических характеристик взаимодействующих тел, а физические – проистекают из естественного разброса свойств материала при ударах. Следствием этого является возникновение разнообразных упрощенных теорий удара [7, 8 и др.].

Правомерность упрощающих предположений проверяют, используя экспериментальные данные. Если и в случае применения упрощенной физической модели аналитическое решение задачи невозможно или чрезвычайно затруднено, используются численные методы [7]. Развитие информационных технологий создает предпо сылки для построения до ста-точно реалистичных моделей соударения численными методами [8].

Численные методы, допуская использование более сложных физических моделей, требуют проверки достоверности результатов математического моделирования. Такая проверка возможна двумя способами [7, 8, 10]:

• 1.    сравнение результатов расчетов с экспериментальными данными;

• 2.    сравнение результатов расчетов по данной модели с результатами расчетов, полученных с применением более точной математической модели. Первый метод представляется наиболее очевидным по известному критерию истины, которым является практика, но имеет недостатки:

• •    требует значительных затрат времени и ресурсов;

• •    требует точного соблюдения значений исследуемых параметров объекта в процессе эксперимента, что не всегда возможно;

• •    имеет неопределенность – к чему относить разницу между результатами расчетов и экспериментальными данными: к погрешности модели, погрешности измерения или влиянию каких-либо неучтенных в эксперименте факторов.

В лесной отрасли отмеченные недостатки усугубляются трудностью подбора однородных объектов для необходимой повторности опытов в эксперименте, т. к. эти объекты имеют природное происхождение, а также ограниченными возможностями варьирования величин факторов в эксперименте [11].

Второй метод требует применения более сложного, чем в проверяемой модели, математического аппарата, который обычно проявляется в необходимости решения систем дифференциальных уравнений с большим количеством элементов. Применение компьютеров облегчает этот процесс [7, 8, 10].

В настоящей работе представлена новая методика [5, 12, 13] моделирования соударения элементов универсальной машины на базе динамического лункообразователя типа Л-2У с препятствиями на вырубке, развивающая ранее выполненные исследования [3, 14].

Целью методики является определение для возможных вариантов соударений рабочих орга- нов машины с препятствиями коэффициентов динамичности, необходимых для проектных и конструкторских работ при создании и совершенствовании динамических лункообразовате-лей и машин на их базе.

Для создания методики использованы аналитические и численные методы, эффективность которых доказана применительно к объектам, работающим в условиях ударных нагрузок [7, 8, 10].

В методике [5, 12, 13] учитывается, что при посадке леса в среде препятствий на вырубке возможны следующие неблагоприятные с точки зрения нагруженности динамического лункооб-разователя ситуации: удар рычага о пень, удар иглой на конце рычага о камень, удар опорного устройства (лыжи) о пень, удар лыжи о камень после преодоления пня. Прочность узлов лунко-образователя должна гарантировать его надежное функционирование в среде естественных препятствий (пней, камней).

При ударе рабочего органа (рычага с иглой) о препятствие потенциальная энергия рабочего органа, накопленная путем напряжения пружины и подъема рычага, преобразуется в кинетическую энергию, которая частично рассеивается в металлоконструкции машины и может вызвать ее поломки (рис. 2).

Уменьшить величину потенциальной энергии можно, но нецелесообразно, т. к. ее величина должна соответствовать кинетической энергии, затрачиваемой на образование лунки. Численное ее значение применительно к различным условиям определено ранее и составляет 1…1,5 кДж [3, 14].

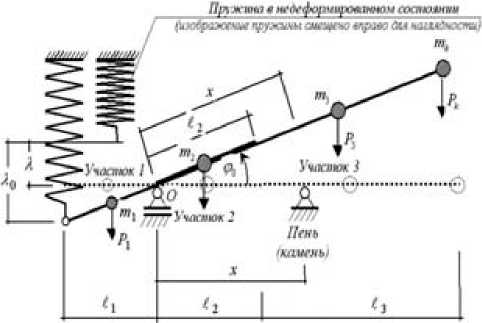
Рис. 2. Расчетная схема динамического лункообразователя

λ , λ 0 – текущее и начальное удлинение пружины, м; φ 0 – угол качания рычага, град.; m 1 , m 2 , m 3 – погонные массы участков рычага, кг/м; m k – масса иглы, кг

Поворот рычага с иглой вокруг оси О (см. рис. 2) под действием собственного веса и силы натяжения пружины можно описать выражением (1), где J – момент инерции рычага, кг·м²; ω – угловая скорость рычага, рад/с; с 0 – коэффициент жесткости пружины, Н/м. Проинтегрировав выражение (1), получим точную величину кинетической энергии E k рабочего органа. Дальнейшими преобразованиями определим угловую скоро сть ω и угловое ускорение ε рабочего органа.

li          ,             12          , f „      13 1,

Jtodto = mig ^ cospdp - m2 g — cospdp - m3 g 112 + — I cos pdp>

^---- m k g ( 1 2 + 1 3 ) cos p d p - c 0 ( Л ) - 1 i ( sin p o - sin p )) 1 i cos p d p ,

_ to2i

E k = J— = ( A - c q 1 i ( A o - 1 1 sin p o )) ( sin p - sin p o ) + 4 c o 1² ( cos ( 2 p ) - cos ( 2 p o )) ;

, li 12 f „

A = m i g "2" - m 2 g ~ - m 3 g 1 1 2 + —

2 Ek

® =      ; £ = ® —;

V Jd

£ = —

J

f m^

. V 2

^^^^^^^s

m 2 l 2 2

^^^^^^^s

f 13 ^                                                     iV12 + TI - mk(12 +13)|" g- co1i(^o - 1ip)] ■ cos p - 2jCo12 sin(2p);

m 3 1 1 2 + -3

I

h                  1 2                    1 2 + 1 3

J = j 5 ² ( m i ds ) + j s ² ( m 2 ds ) + j s ² ( m 3 ds ) + m k ( 1 2 + 1 3 ) 2 =

l 2

m i 1³ + m 2 1 2 + m 3 ( ( 1 2 + 1 3 ) 3 - 1 2 ) 3

+ m k ( 1 2 + 1 3 ) 2 .

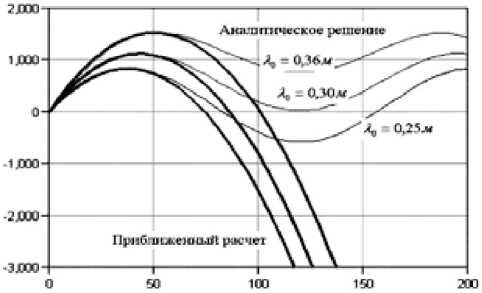
Рис. 3. Изменение кинетической энергии Ek

E k , Дж, в зависимости от угла поворота рычага φ = 0…200 ⁰ (система технологически пригодна, если λ0≥0,30 м, тогда 0k≤1500 Дж)

плоскостью и плоскостью лыжи, град.; Δ – перемещение лыжи при соударении с пнем, м, обусловлено деформацией пня; k din – коэффициент динамичности; N – сила контактного взаимодействия, Н; k s – приведенный коэффициент жесткости системы «лыжа-пень», Н/м (коэффициент жесткости пня определялся экспериментально – 18…46·106 Н/м).

Коэффициент динамичности получим, найдя положительный (с учетом физического смысла задачи) корень уравнения, выражаемого из равенства (6):

k din

mg cos у

N

1 +

V

k s v ²

¹ + 7 tg 2 Y mg ²

A

Результаты расчетов по формулам (2…5) в разработанной программе для ПЭВМ в среде «Maple» [15] для динамического лункообразователя Л-2У [3] показаны на рис. 3.

Проверка модели (2…5) осуществлялась последовательным выполнением приближенного и точного расчетов. Приближенный расчет обеспечил полную сходимость с аналитическим решением при угле поворота рычага до 600, в реальном диапазоне для динамического лункообразователя типа Л-2У (рис. 3).

Для исследования нагруженности рычага динамического лункообразователя при соударении с препятствием (пнем, камнем) рычаг моделируется балкой с пролетом х (рис. 2), материал которой подчиняется закону Гука.

Для исследования поведения балки при соударении с опорами использован метод конечных разностей, а для проверки его применимости к условиям задачи – метод конечных элементов, реализованные в программе для ПЭВМ в среде «Maple» [15].

Установлено, что при ударе иглой на конце рычага Л-2У о камень коэффициент динамичности равен 465, а напряжение изгиба 276 МПа. При ударе серединой рычага о пень коэффициент динамичности равен 103, а напряжение изгиба 265 МПа. Высокие значения коэффициентов динамичности показывают, что масса машины используется наилучшим образом для совершения работы, характеризуя ресурсосбережение при использовании динамического принципа образования лунок. Требования к качеству материалов при этом растут.

Уравнение баланса энергии при соударении опорного устройства (лыжи) лункообразователя с пнем (рис. 4) имеет вид:

Моделирование соударения лыжи с пнем в программе для ПЭВМ в среде «Maple» [16] выявило, что с увеличением угла наклона лыжи и скорости движения агрегата возрастают силы динамического взаимодействия (рис. 5). Рекомендуемый угол наклона лыжи составляет 33…570, при допустимой нагрузке в навесном устройстве трактора ЛХТ-55 или ЛХТ-100 не более 40 кН.

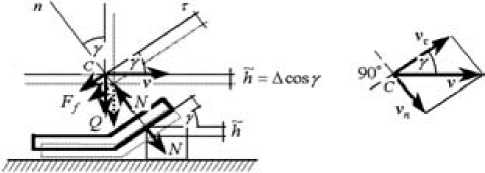
Рис. 4. Расчетная схема соударения лыжи с пнем

F f – сила трения, Н; Q – вес лыжи и части машины, Н; точка С находится в области контакта опорной лыжи с пнем

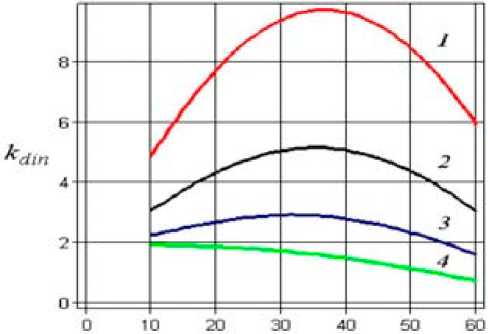
Угол наклона опорной лыжи в градусах

Рис. 5. Зависимость коэффициента динамичности от угла наклона лыжи и скорости агрегата

mv2 sin2 у     .,N

---- ----+ mgAkdin cos Y = — kdin,(6)

где m – масса лыжи и части машины, кг; v – скорость агрегата, м/с ; γ – угол, образованный горизонтальной

Кривые 1…4 построены для скорости агрегата равной 1,0; 0,5;

0,25 и 0,1 м/с соответственно

Завершающей стадией взаимодействия с неподвижным препятствием (пнем) является свободное падение лыжи с присоединенной частью массы лункообразователя с высоты пня Н на почву или камень. Уравнение баланса энергии в этой ситуации будет выглядеть так:

mv2 _ Ndin A din

где m – масса лыжи с присоединенной частью массы машины, кг; v – скорость свободного падения, м/с; N din – сила контактного взаимодействия, Н; Δ din – перемещение по направлению силы N din , м.

При упругом соударении сила N din и перемещение Δ din связаны так:

а.

N din _ k s A din ; N din _ v^mk s ,       (9)

где k s – коэффициент жесткости лыжи в вертикальном направлении (при падении лыжи на камень как абсолютно жесткое тело) или приведенный коэффициент жесткости системы «лыжа-почва» (при падении лыжи на почву).

Зная коэффициенты жесткости k s^лыжи и k s^почвы , найдем коэффициент динамичности k din при свободном падении лыжи и соударении с почвой или камнем:

v mk s k din —            ,

mg

Коэффициент k_s ^почвы получим, найдя положительный корень уравнения, выражаемого из соотношений (8) и (9), с учетом известного выражения [2] для определения силы сопротивления внедрения в почву деформатора произвольной формы:

кпочвы _

S b '[ 5 cm ] +

S b '[ 5 cm ]

2• v • ^Jm    vk 2' v'^m

V

2            У

I + P ' f '[ 5 CM ]

где S в – площадь верхнего основания деформатора (лыжи), м²; Р – периметр основания деформатора, м; f – коэффициент трения «сталь-почва».

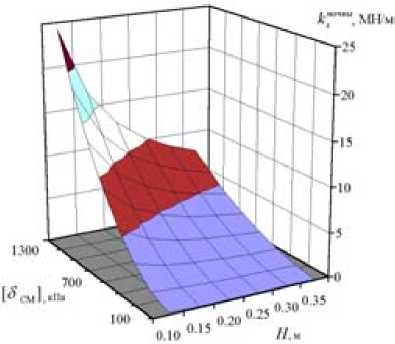
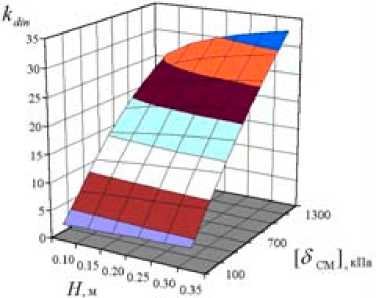
Расчеты по формулам (8…11) выполняются в «Mathcad». Результаты представлены на рис. 6.

При работе универсальной машины на базе лункообразователя в режиме посева возможны следующие неблагоприятные с точки зрения нагруженности ситуации: удар колеса о пень, падение колеса с высоты преодолеваемого пня.

Уравнение баланса энергии при соударении колеса высевающего приспособления с пнем (рис. 7) запишется аналогично (6):

mv2 cos2 a

---- ----+ mgAkdin sin a — — kdin , где m – масса высевающего приспособления, кг.

б.

Рис. 6. Параметры процесса падения лыжи с пня а – коэффициент жесткости почвы k s^почвы ; б – коэффициент динамичности k_din

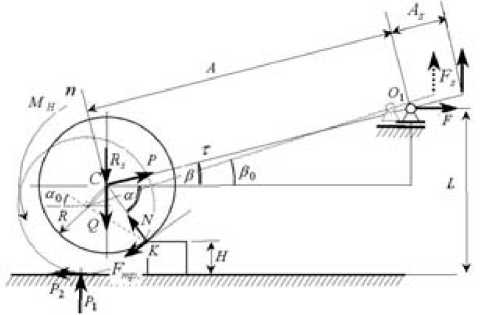
Рис. 7. Модель секции высевающего приспособления

H – высота пня, м; R – радиус жесткого опорно-приводного колеса, м; A и A s – длины звеньев рычага, м; F – сила тяги трактора, Н; P – продольная сила в звене CO 1 , Н; Q – вес, передаваемый на ось колеса, Н; F s – сила растяжения пружины, Н; k s – коэффициент жесткости пружины, Н/м; N – нормальная составляющая силы взаимодействия колеса с пнем, Н; F тр = f N – сила трения в области контакта колеса с пнем, Н; f – коэффициент трения скольжения в этой области; M H = μ N – момент трения качения, Н; μ – коэффициент трения качения; P 1 – реакция почвы, Н; P 2 – сила трения в области контакта с почвой, Н

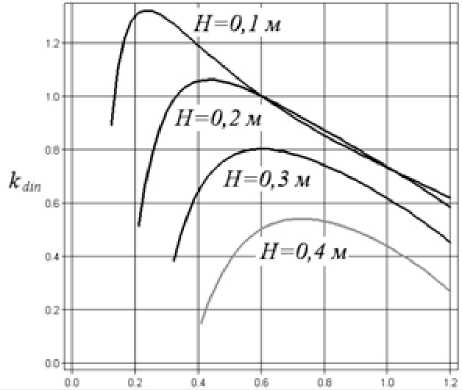
Рис. 8. Зависимость k _din от радиуса колеса R , м

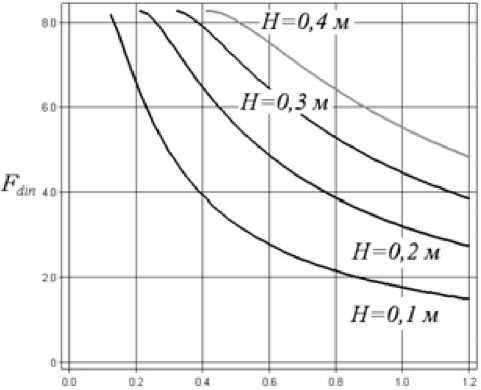
Рис. 9. Зависимость силы F _din , Н от радиуса колеса R , м

Коэффициент динамичности получим, найдя положительный корень уравнения, выражаемого из соотношения (12):

k s v ²

mg sin a k din —

N

¹⁺1^{1 +}     2 2    ,

\ mg2 tg 2a ,

к

Анализ расчетов в программе для ПЭВМ в среде «Maple» [17] показал, что коэффициент k din растет при уменьшении высоты пня (рис. 8 и 9). При этом теоретическая величина силы F dyn = F·k dyn также убывает; следовательно, для преодоления пня бóльшей высоты необходим трактор с бóльшей силой тяги, что соответствует практике.

Моделирование падения колеса высевающего приспособления с высоты преодолеваемого пня выполняется с помощью формул (8…10). Коэффициент же стко сти почвы k s^почвы определяется численно (в «Mathcad») из уравнения (14), где L p – ширина реборды колеса, м.

Масса m определяется выражением (15), где m пр – приведенная масса рычага и секции приспособления, кг; k s – коэффициент жесткости пружины рычага, Н/м; λ – перемещение пружины, соответствующее перемещению приведенной массы, м; S – остаточное натяжение пружины в позиции, когда колесо оперлось о почву (камень), м.

[ 5 cm ] ■

f I ² g ■ H ■ m

L p + 1

к У    к^ почвы

■ fv 2 2 R

2 g ■ H ■ m 2 g ■ H ■ m

^^^^^^»

m —

k_s почвы

k_s почвы

+ 2 L_p ■   ^{2 g} ■ H ■ m ■ f I - 4 2 g ■ H ■ m ■ к п' ^очвы — 0 ,⁽¹⁴⁾

р почвы ks             )

m пр

■ g ■ h + k s XA ^ + s

gH

; я —

H ■ A s

A

ВЫВОДЫ:

• 1.    Представленная методика рекомендуется для оптимального проектирования машины для лесовосстановления на базе лункообра-зователя типа Л–2У.

• 2.    Расчеты по представленной методике для машины на базе лункообразователя Л–2У

показали, что при работе на вырубке в диапазоне скоростей 1,8…3,6 км/ч возникают ударные нагрузки, которые характеризуются коэффициентами динамичности: от 1,1 (наезд колесом на пень) до 465 (удар рычагом о камень).