Моделирование нагрузки ленточного конвейера роторного экскаватора большой единичной мощности

При моделировании нагрузки конвейерной техники непрерывного действия следует учитывать большое количество различных факторов.

Распределенная нагрузка перемещаемой конвейером горной массы, а также вес самой ленты создают нагрузку на опорные ролики, определяющие возрастание усилия в ленте пропорционально длине нагруженного участка [1]. В данной статье рассматриваются факторы, влияющие на нагружение ленточного конвейера, и формулы, позволяющие моделировать эти факторы на этапе проектирования данной системы.

Математическое моделирование нагрузки конвейера роторного экскаватора

Следует учитывать, что если конвейер работает в наклонном положении, возникает составляющая силы веса, воспринимаемая лентой на данном участке конвейера. В этом случае удельное усилие в ленте на загруженном участке, связанное с действием весовой нагрузки (рис. 1), определяется следующим образом:

Fg( l ) = (g + g 0 ) (K оп ⋅ cos β KJI + sin β KJI ),                                (1)

где g – вес породы на 1 м ленты;

g0 – вес 1 м ленты;

K оп – коэффициент удельного сопротивления опорных устройств.

Величину g определяем из следующего соотношения:

g = Q T ⋅ ρ /3600V К ⋅ K p ,

где Q T – текущее значение производительности экскаватора;

VK – скорость движения ленты конвейера;

K p – коэффициент разрыхления горной массы.

Сопротивление, создаваемое очистительными устройствами, которые удаляют прилипшую на конвейере породу, определяем следующим образом:

F₀₄ = q₀₄ ⋅ β.                                                      (3)

Усилие, необходимое для перегиба ленты и преодоления трения в подшипниках барабана, получаем из следующего соотношения:

F = K из ⋅ β,

где Kиз – коэффициент, зависящий от ширины барабана.

Величину мощности для сообщения поступающей горной массе дополнительной кинетической энергии получим из выражения

Ркин = m (V - VЭ) /2,                                (5) где VK – скорость движения ленты конвейера;

V Э – скорость экскавации.

Определяем количество движения (импульс тела):

Суммарный выражения m^V22 -V2) FКИН =( 2VK ).                                       (6) момент сил статического сопротивления движению ленты определяем из м.. = ^^ «..                   (7) где FНБ – сила натяжения барабана;

F_СБ – сила скольжения барабана;

а _Б - диаметр барабана.

Величину суммарной расчетной мощности двигателей конвейера получим по формуле м, • W.

Р дкл = К 3 —-~

.             п р

Угловая скорость барабана конвейерной линии и линейная скорость конвейерной ленты связаны соотношением

W _S K КЛ

= 2 V K

^а Б

В данном случае коэффициент запаса К3 вводится для учета неравномерности распределения нагрузки между двигателями.

Угловые скорости приводных двигателей и барабана конвейера связаны между собой выражением

W₅ Kкл = W₈ кл • i ,                                       (10)

где i – передаточное отношение привода барабана.

Для моделирования срабатывания упругих муфт выполняется анализ

” 5 . кл — ''л . ллм"

Кроме того, в моменте сопротивления движению ленты необходимо учитывать момент от электромагнитных тормозов на быстроходных валах передач.

Приводы поворота и конвейерной линии разгрузочной консоли роторного экскаватора

В этом случае при работе механизмов поворота стрелы ротора и разгрузочной консоли при моделировании сил, моментов и скоростей описываются теми же уравнениями. Эти же соображения позволяют использовать для моделирования работы конвейерной линии разгрузочной консоли уравнения (1-10), записанные для ленточного конвейера ротора.

Механизмы привода хода экскаватора

Статическая нагрузка привода шагающе-рельсового хода при перемещении экскаватора определяется следующими имеющимися факторами: трением качения ходовых колес; трением в подшипниках ходовых колес; преодолением скатывающей силы при негоризонтальном положении (установке) лыжи; действием ветрового напора; сопротивлением горной массы при врезке роторного колеса подачей на забой [2].

Схема усилий механизма хода приведена на рис. 2 (одна из имеющихся четырех лыж роторного экскаватора).

В этом случае составляющая натяжения тягового каната от сил трения при допущении о равномерном распределении нагрузки на ходовые тележки из учета К П Д полиспаста определяется следующим образом:

G cos р 2 ц+а_ц • f к

,

1 Т • К • ТР       .    .           п ТР-ГР jr • in        Dk где jT – число ходовых тележек;

• i_n – кратность полиспаста;

• f к , μ – соответственно, коэффициенты трения качения и трения скольжения;

• α_Ц – диаметр цапфы подшипника;

D_k – диаметр ходового колеса.

Выводы

Уравнения, представленные в данной статье, позволяют моделировать факторы и нагрузки, влияющие на работу не только ленточного конвейера роторного экскаватора, но и разгру- – 339 –

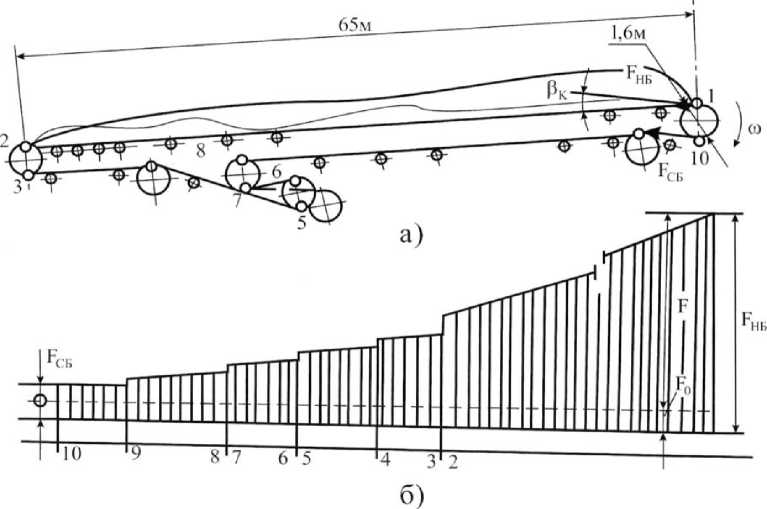
Рис. 1. Схема конвейера стрелы ротора

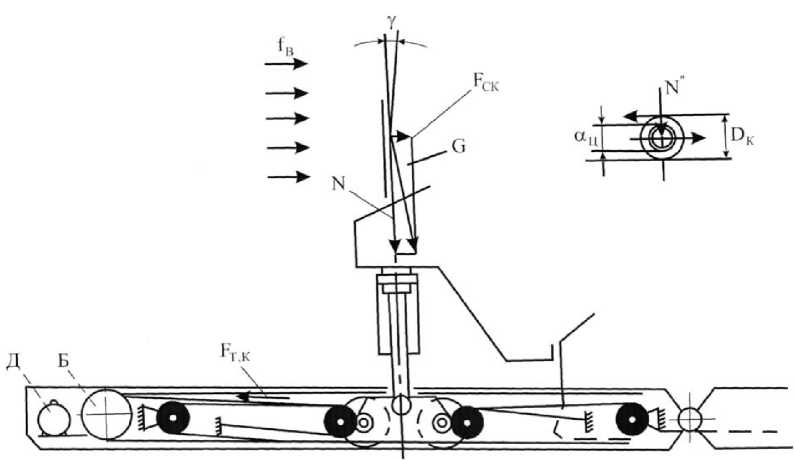
Рис. 2. Схема усилий механизма хода зочной консоли и поворота стрелы ротора, что, несомненно, упрощает процесс моделирования и проектирования систем роторных экскаваторов.