Моделирование напорной характеристики центробежной компрессорной ступени

Несмотря на быстрое развитие методов вычислительной газодинамики, инженерные методики проектирования и расчета центробежных компрессоров не теряют актуальности, а все более востребованы. Их совершенствованию уделяют внимание и отечественные, и зарубежные специалисты [17]. Важно иметь надежный математический аппарат для расчета газодинамических характеристик ступени с любой практически применимой проточной частью.

Формально задача не является сложной. Достаточна возможность рассчитать КПД и ко -эффициент внутреннего напора в зависимости от условного коэффициента расхода, которым пользуется Политехническая школа [4] и ряд зарубежных специалистов, или одним из физических коэффициентов расхода, который предпочитают другие. Однако практически решение представляется достаточно сложным. Например, авторы новых версий Метода универсального моделирования для расчета коэффициентов потерь используют более двух десятков алгебраических уравнений с 65 эмпирическими коэффициентами [8, 9]. Система алгебраических уравнений базируется на физической схеме течения, т.е. на нескольких экспериментально подтвержденных или построенных логически допущениях. Причинами потерь напора считается трение газа о поверхности проточной части и вихревые потери, возникающие при отрыве пограничного слоя на участках замедленного течения. На основе результатов визуализации принято, что вихревые потери в рабочем колесе могут появляться только на стороне разрежения рабочих лопаток, и т.д. Математические модели такого рода носят, по существу, произвольный характер, отражающий взгляды разработчика в тот или иной момент.

Следует отдать должное создателям упомянутых инженерных методов [17], преодолевших значительные трудности и с успехом применяющих компьютерные программы на базе математических моделей в проектной практике. Авторы настоящего текста полагают, что развитие прикладной математики и вычислительной техники сделало актуальным применение альтернативного способа расчета характеристик центробежных компрессорных ступеней. Программные пакеты для построения нейросетей дают возможность создания математических моделей, не прибегая к построению физических моделей и их математическому описанию. Попытки такого рода представлены в публикациях [10-12]. Характеристики КПД и коэффициента политропного напора большого количества разнообразных ступеней моделируются с точностью, соизмеримой с точностью экспериментального определения характеристик. Достаточно успешны и результаты моделирования параметра эффективности безлопаточных диффузоров. Нейронными сетями смоделированы характеристики коэффициента трения серии безлопаточ-ных диффузоров, определенные CFD-расчетами.

Можно полагать, что «нейронные» модели пригодны для решения прямой задачи газодинамики – расчет газодинамических характеристик центробежной ступени с заданными размерами при заданных начальных условиях. «Физические» математические модели решают и обратную задачу – позволяют найти оптимальную форму проточной части, при которой заданные расход и конечное давление будут получены при максимальном КПД. За счет быстродействия программы Метода универсального моделирования [4] выполняют эту работу перебором вариантов. Опыта успешного применения «нейронных» моделей для решения подобной задачи пока нет. Будущие исследования дадут ответ на этот вопрос. Настоящий текст посвящен более простой задаче – моделированию напорной характеристики центробежной компрессорной ступени.

В безразмерном виде по результатам испытания характеристики ступени удобно представлять как:

n >, = f(ф).

В соответствии с известными соотношениями между безразмерными и размерными па-

раметрами:

– массовый расход

p ^*     3,141

m = -5-0* ф ---D 2 u 2 ;

RT0    4

– отношение давлений

pM + ( k - 1 ) ^ i M U ) , p ^* ₀

где M u =

u₂ kRT 0^*

– мощность привода ступени

n,=m,д = ф^ p ^'d...                             (4)

RT0 4

Авторы разработали нейронную модель характеристики внутреннего напора у i = f ( Ф ) . Для идентификации (применительно к нейтронным сетям процесс называют обучением) использованы характеристики внутреннего напора центробежных компрессорных ступеней промежуточного типа РК+БЛД+ОНА. Обработаны результаты испытаний трех групп модельных ступеней:

• –    компании «Dresser&Clark» (США), лицензия на которые была приобретена в 1970-е гг.;

• –    проблемной лаборатории компрессоростроения ЛПИ [13, 14];

• –    Невского машиностроительного завода.

Проточная часть ступеней состоит из рабочего колеса с радиально расположенными лопатками цилиндрической формы, безлопаточного диффузора. На рис. 1 показана схема, общая для всех 39 ступеней, участвовавших в идентификации.

Соотношения размеров количество лопаток и лопаточные углы ступеней лежат в широком диапазоне. Границы изменения конструктивных параметров ступеней, выбранных для идентификации моделей, указаны в табл. 1.

Величина коэффициента напора определяется соотношениями размеров рабочего колеса, формой и количеством лопаток. В монографии [14] приведены экспериментальные данные, которые указывают на влияние формы диффузора на коэффициент напора. Имеет место влияние последующего элемента проточной части на работу предшествующего. Поэтому в таблице приведены геометрические соотношения всех элементов проточной части. В процессе идентификации соотношения размеров ОНА получили низкие весовые коэффициенты, поскольку этот элемент значительно удален от рабочего колеса и не оказывает на него влияния.

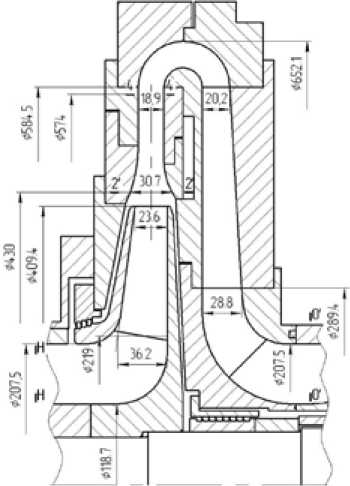
Рис. 1. Схема модельной ступени проблемной лаборатории компрессоростроения ЛПИ

Экспериментальные исследования ступеней при различных условных числах Маха в диапазоне Mu = 0,327-0,920 позволили получить данные по 101 газодинамической характеристике КПД и напора. В каждой из них внутренний напор измерялся в 46 точках по расходу. Таким образом, выборка исходных данных для идентификации модели составила 567 наборов значений.

Представленный выше набор ступеней, помимо широкого диапазона геометрических размеров, имеет достаточно плотную детализацию промежуточных значений. Внутри диапазонов геометрических параметров (табл. 1) содержится большое количество их значений, например:

• –    ряд чисел лопаток: 13; 15; 17; 18; 19; 20; 21;

• –    ряд выходных углов лопаток РК β Л2 = 22,5°; 27,8°; 35,01°; 37°; 40,5°; 8,49°; 52,1°; 56,9°;

о

,;

• –    ряд входных углов лопаток β Л1 = 24,39°; 28,6°; 29,4°; 33,45°; 34,4°; 37,39°; 37,41°; 37,47°; 37,61°;

• –    ряд условных чисел Маха M u = 0,327; 0,36; 0,589; 0,6; 0,601; 0,603; 0,604; 0,605; 0,648; 0,66; 0,785; 0,79; 0,791; 0,792; 0,793; 0,794; 0,795; 0,796; 0,798; 0,864; 0,917; 0,919; 0,92.

Условный коэффициент расхода Ф охватывает диапазон значений от 0,0024 до 0,126, распределенных достаточно равномерно. На область от 0,0024 до 0,05 приходится 421 из 567 точек характеристик.

Представленные в исходной выборке данные описывают ступени с политропным КПД η от 0,33 до 0,848 и коэффициентом политропного напора ψ i в диапазоне от 0,051 до 0,618.

В ходе работы была поставлена задача создать модель, рассчитывающую внутренний напор ψ i в виде зависимостей f (Ф ,M u ,,G ) от условного коэффициента расхода, условного числа Маха и совокупности параметров, описывающих геометрию проточной части (обозначены как G ).

Таблица 1. Диапазон значений геометрических параметров ступеней

Название параметра	Обозначение	Минимум	Максимум
Относительный диаметр втулки	D ВТ /D 2	0,25	0,3916
Относительный диаметр уплотнения	DУП/D2	0,436	0,592
Число лопаток РК	zРК	13	21
Относительная толщина лопатки РК	δ РК /D 2	0,007	0,017
Относительный диаметр в сечении ступени 0-0	D0/D2	0,425	0,573
Относительный диаметр на входе в РК	D 1 /D 2	0,502	0,668
Относительная высота лопатки на входе в РК	b 1 /D 2	0,0063	0,124
Относительная высота лопатки на выходе из РК	b 2 /D 2	0,0063	0,069
Угол установки лопатки β л1на входе в РК	β L1	24,39°	37,61°
Угол установки лопатки β л2 на выходе из РК	β Л2	22,5°	85,5°
Относительный радиус закругления основного диска РК	R S1 /D 2	0	0,128
Относительный радиус закругления покрывного диска РК	R S2 /D 2	0	0,0653
Относительный диаметр на входе в БЛД	D 3 /D 2	1,01	1,05
Относительный диаметр на выходе из БЛД	D 4 /D 2	1,41	1,56
Относительная ширина проточной части на входе в БЛД	b 3 /D 2	0,0056	0,069
Относительная ширина проточной части на выходе из БЛД	b 4 /D 2	0,0056	0,069
Относительный диаметр входа в лопаточную решетку ОНА	D 5 /D 2	1,41	1,56
Относительный диаметр выхода из лопаточной решетки ОНА	D 6 /D 2	0,577	0,818
Относительная ширина проточной части на входе ОНА	b 5 /D 2	0,033	0,085
Относительная ширина проточной части на выходе ОНА	b 6 /D 2	0,033	0,085
Относительный диаметр проточной части на выходе из ступени	D 0, /D 2	0,475	0,625
Относительный внешний радиус поворотного колена	R 3 /D 2	0,0716	0,159
Относительный внутренний радиус поворотного колена	R 4 /D 2	0,032	0,0739
Угол установки лопатки α Л5 (в градусах) на входе в ОНА	α Л5	8,6	37
Число лопаток ОНА	z ОНА	16	32
Относительная толщина лопаток ОНА	δ ОНА /D 2	0,028	0,057

На подготовительном этапе было создано несколько видов моделей с разной структурой нейронной сети и параметрами обучения. Из них были выбрана сеть с наименьшей средней квадратичной ошибкой.

Для моделирования значений внутреннего напора использовалась сеть, состоящая из двух слоев, 20 нейронов в первом слое и 1 нейрона – во втором. Функции активации слоев нейронов в моделях: logsig (логическая сигмоида) для первого слоя и pureline (линейная) для второго слоя.

При анализе результатов выяснилась специфическая особенность экспериментальных характеристик лицензионных и отечественных ступеней. Типичный пример характеристик η^*, ψ i = f(Ф) отечественной модельной ступени показан на рис. 2.

Графики демонстрируют минимальный разброс точек относительно линейной зависимости η^*, ψ i = f(Ф).

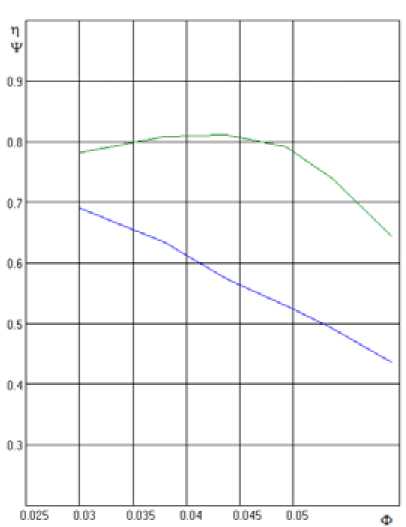
Рис. 2. Пример характеристикимодельной ступени в координатах n * , V i = f(Ф)

Характеристики лицензионных ступеней представлены в виде зависимостей n * , V i = f(Ф)■

Коэффициент политропного напора связан с коэффициентом внутреннего напора через КПД:

V i = *■ n

.

Для лицензионных ступеней внутренний напор получен из исходных данных отношением коэффициента напора к политропному КПД по соотношению (5). На значительный разброс точек на графиках КПД и коэффициента политропного напора некоторых сверхмалорасходных ступеней не обращали внимания, так как в целом зависимости не противоречили известным закономерностям. Но у этой части ступеней получился незакономерный и значительный разброс относительно линейной зависимости. Характерные примеры представлены на рис. 3.

На рис. 3 приведены характеристики двух близких по параметрам сверхмалорасходных ступеней с различным отклонением от линейной зависимости n * , V i = f(Ф). Трудности корректного измерения параметров потока при испытаниях сверхмалорасходных ступеней очевидны, но не исключают возможности корректных измерений. На рис. 4 показаны характеристики сверхмалорасходной ступени и среднерасходной ступени с корректно измеренной характеристикой n * , V i = ^(Ф).

Средняя ошибка по всем 567 входным векторам обучающей выборки расчётных значений внутреннего напора у i = f( G, Ф , M u ) составила 1,83 %. Если не учитывать крайние по расходу точки, то среднее отклонение расчётных значений внутреннего напора на оптимальных режимах не превышает 1,5 %. Без ступеней с некорректно измеренными коэффициентами напора

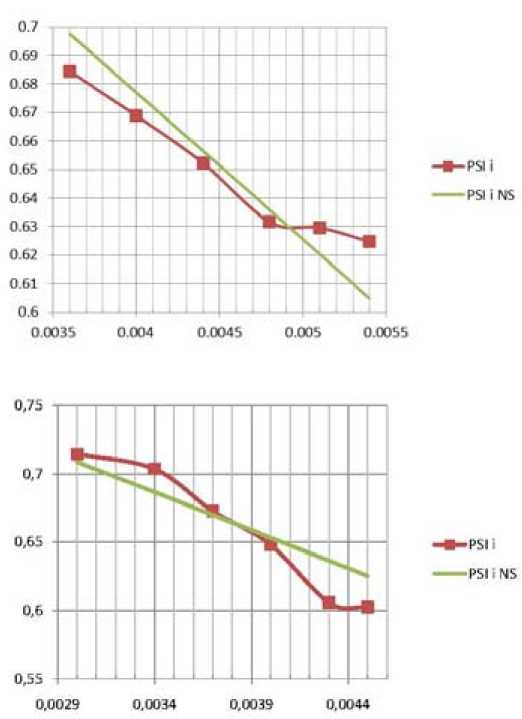
Рис. 3. Примеры измеренных с большой погрешностью характеристик n*, Vi = f(Ф) лицензионных ступеней фирмы Dresser-Clark и результат моделирования отклонение уменьшается до 0,7 %, что соизмеримо с погрешностью тщательно проведенных экспериментов.

Авторы обращают внимание разработчиков инженерных проектировочных программ на полученный результат. В работе [14] представлены результаты моделирования напорной характеристики коэффициента теоретического напора на основе «физической» модели. Сопоставление показывает следующее:

• –    нейронное моделирование обеспечило более высокую точность для гораздо большей количественно выборки ступеней и с гораздо большим диапазоном коэффициентов напора и расхода;

• –    технически получить результат при нейронном моделировании проще. Авторам работы [15] пришлось не только использовать результаты экспериментов с модельными ступенями, но также воспользоваться ранее проведенными численными экспериментами – расчетами напорных характеристик рабочих колес при невязком обтекании [16, 17].

Вместе с тем следует отметить определенную опасность некритичного использования математических методов без анализа физической сущности получаемых результатов. На рис. 5

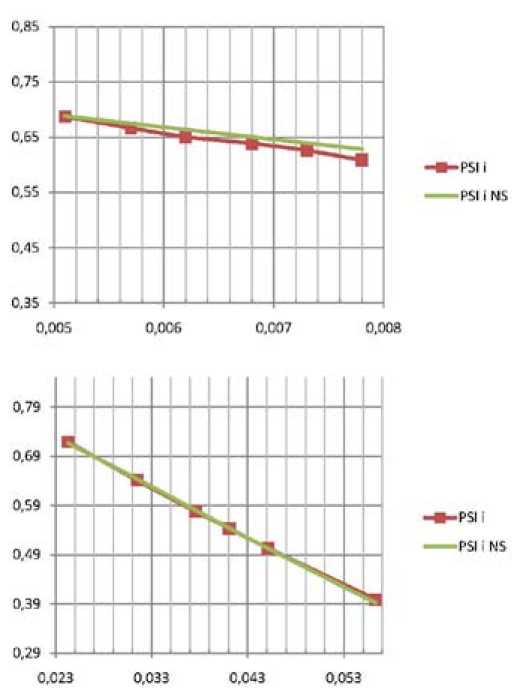
Рис. 4. Примеры корректно измеренных характеристик n * , V i = f(Ф) и результат моделирования

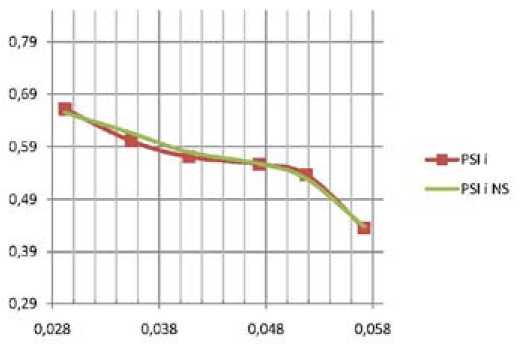
Рис. 5. Пример некорректно измеренной характеристики n*, Vi = f(Ф) среднерасходной ступени и результат моделирования приведена некорректно измеренная характеристика η*, ψi = f(Ф) среднерасходной ступени и результат моделирования.

Несмотря на явную ошибку измерений, нейронная модель точно повторила результаты ошибочного эксперимента. В данном случае ошибка измерений и моделирования очевидна, и виден путь предотвращения подобной ошибки. При моделировании характеристики КПД подобное труднее выявить и устранить. Нейронное моделирование газодинамических характеристик центробежных ступеней следует продолжить и тщательно проанализировать.

Исследование выполнено при финансовой поддержке Российского фонда фундаментальных исследований, Правительства Красноярского края, Красноярского краевого фонда поддержки научной и научно-технической деятельности в рамках научного проекта № 16-41-242156 р_офи_м