Моделирование напряженно-деформированного состояния при осадке высокой полосы (двухстороннее течение металла)

Процесс осадки высокой полосы в чистом виде при обработке металлов давлением встречается достаточно редко. Однако в ряде случаев при математическом моделировании путем замены переменных реальные процессы могут быть сведены к моделированию этого процесса. Например, с помощью конформного отображения Z = P e^{l Ф} декартова система координат может быть преобразована в цилиндрическую (здесь £ представляет собой круговую область; р и ф - цилиндрические координаты, рассматриваемые в декартовой системе координат; l - мнимая единица) [1]. В этом случае процесс высадки концов труб, применяемый при отделке труб нефтяного сортамента [2], может быть математически описан как процесс осадки высокой полосы.

Особенностью математического описания процесса осадки высокой полосы является то, что граница очага деформации заранее неизвестна. Наряду с этим следует отметить, что процесс осуществляется в горячем состоянии, а схема течения металла после конформного отображения представляет собой плоскопараллельное течение. Благодаря отмеченным особенностям для моделирования напряженно-деформированного состояния при осадке высокой полосы наиболее предпочтительным является метод линий скольжения [3].

Процесс высадки концов труб может осуще- ствляться как с двухсторонним, так и с односторонним течением металла в радиальном направлении. Соответственно, заменяя задачу анализа процесса высадки концов труб на задачу осадки высокой полосы, необходимо рассматривать две различные схемы течения металла. В данной работе рассмотрим более общий случай осадки с двусторонним течением, расчетная схема для которого и сетка линий скольжения представлены на рис. 1.

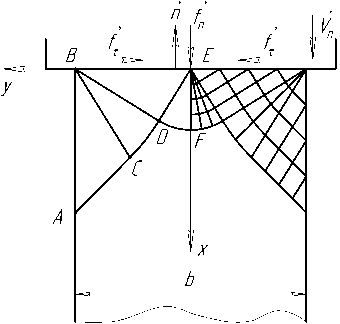
Рис. 1. Расчетная схема для моделирования процесса осадки высокой полосы

В связи с симметрией процесса рассмотрим половину очага деформации, ограниченную кон-

Выдрин А.В., Зинченко А.В., Баричко Б.В.

Моделирование напряженно-деформированного состояния при осадке высокой полосы (двухстороннее течение металла)

туром ABEFDCA . Сетку линий скольжения представим в виде прямоугольных треугольников ABC и BDE и двух центрированных вееров BCD и DEF .

Линиями скольжения семейства α будем считать линии BC , BD , DF . Соответственно линии AC , CD , DE , EF будут линиями семейства β.

Определение напряженно-деформированного

состояния начнем с рассмотрения треугольника ABC . В качестве граничных условий для области ABC рассмотрим условия контура АВ . Это поверхность свободная от внешних нагрузок, следова-

тельно, в соответствии с граничными условиями метода линий скольжения для всех точек М облас-

пряжение в которой определяется выражением (2). Это говорит о том, что значения напряжения σ по (2) и (3) можно приравнять друг к другу, в результате чего определится величина нормального напряжения fn =т5 {П — 1 + arccos(-^) — sin [arccos(-^)]j • (4)

Выражение (4) может быть использовано в технологических расчетах для определения нормального контактного напряжения в начальный момент процесса высадки. В качестве примера на рис. 2 показана зависимость нормального напряжения от величины коэффициента трения (τ s = 1).

ти АВС получим:

„          , 3

ф = const = -п

о = const = -т 5

∀ M ∈ Δ ABC .

Граничные условия в напряжениях также известны для контура ВЕ . На этой поверхности действует вектор нормального напряжения f_n и век-

тор касательного напряжения f _τ . Величина вектора f_n пока неизвестна и подлежит определению. Вектор касательного напряжения является вектором напряжения трения. Поскольку рассматриваемый процесс осадки осуществляется в горячем состоянии, модуль вектора напряжения трения можно определить по формуле Зибеля:

|Л|=—^Т5 , где µ – коэффициент трения; τs – сопротивление металла пластической деформации сдвига. Тогда угол φ для области BDE

ϕ = const =π- 12 arccos( -μ ) ∀ M ∈ BDE .

В свою очередь, среднее нормальное напряжение σ будет равно

σ = const = f_n +τ _s sin [ arccos( -μ ) ] ∀ M ∈ BDE . (2)

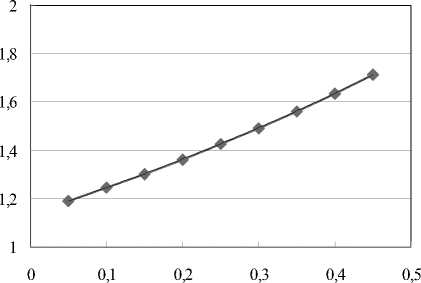
Коэффициент трения

Рис. 2. Влияние коэффициента трения на нормальное контактное напряжение

Для центрированного веера BCD имеем классическую вырожденную задачу Римана. В данном случае известны параметры σ и φ на луче ВС , которые определяются по выражениям (1), и угол раскрытия веера Δφ, равный разности углов φ для областей АВС и BDE :

Классическая выраженная задача Римана может быть решена для центрированного веера DEF . При этом известны параметры σ и φ на луче DE , поскольку он является стороной треугольника BDE . Из рис. 1 видно, что на луче EF значение угла φ равно π 2 , т. е.

ϕ=π 2 ∀ M ∈ EF .

С учетом этого из уравнений Генки при движении вдоль линии скольжения семейства α DF получим

σ=τ

s

2arccos( -μ ) -

π

∀ M ∈ EF .

π 1

Δϕ = 4 - 2arccos( -μ ) .

Выражение для σ на луче BD получаем с учетом уравнений Генки при переходе от луча ВС к лучу BD вдоль линии скольжения семейства β – CD . С учетом этого имеем

-τ + 2τ π = σ + 2τ ss4s

откуда

σ=τ

s

π- 2 arccos( -μ )

π

2 + arccos( -μ ) - 1

∀ M ∈ BD .

С другой стороны, луч BD является стороной треугольной области BDE , среднее нормальное на-

Таким образом, формулы (1)–(3), (5) определяют напряженное состояние при осадке высокой полосы с трением на контактной поверхности.

Рассмотрим кинематику течения металла в области, ограниченной контуром ABEFDCA . Для этой области с точки зрения кинематических граничных условий известно только то, что контактная поверхность пуансона перемещается в направлении оси ОХ с заданной скоростью V_n . С учетом этого в результате анализа сетки линий скольжения, представленной на рис. 1, можно отметить, что отрезок линии скольжения EF перемещается в направлении оси ОХ также со скоростью V_n . Поскольку отрезок EF представляет собой линию скольжения семейства β, можно отметить, что

Va = 0 | VM e EF.

V e = V n

Определим компоненты вектора скорости точки D. Для этого запишем в конечных разностях уравнение Гейрингер для перехода вдоль линии скольжения семейства α от точки F к точке D vF)-vD)-2 (vy)+с))И)-<и-о и уравнение Гейрингер для перехода вдоль линии скольжения семейства β от точки Е к точке D veE’ - <’+ | (v E)+va D’K’-r)-о.

Решая совместно эти два уравнения, получим:

V (D >=7Г     arCCos(-H) -K va       2v n             r                     ..2 ;

4 + 0,25 [ arccos( -p) - n ]

v ( ^D ) = v_w

1 - 0,0625 [ arccos( -^ ) - n ] ²

1 + 0,0625 [ arccos( -^ ) - n ] ²

Поскольку в области BDE линии скольжения приняты прямыми, т. е. область BDE перемещается как жесткое тело, формулы (6) и (7) определяют скорость перемещения любой частицы в области BDE , в том числе и на линии BD .

Следующим шагом определим компоненты вектора скорости точки С . По аналогии с рассмотренной выше методикой запишем в конечных разностях уравнение Гейрингер для перехода вдоль линии скольжения семейства α от точки В к точке С

v ( B ’ - v s C ’ - 1 ( V ’ + v C ¹ )( t ^{, b} ’ -v ' C ’ ) = 0

и уравнение Гейрингер для перехода вдоль линии скольжения семейства β от точки D к точке С vD) - v C) +1 (vD ’+vC) )(v'd )-V(C) )-0.

В результате совместного решения этих двух уравнений получим:

v(C) = v |     arccos(-H)-n     x a n [ 4 + 0,25[arccos(-H) - n]2

_x 2 - 0,5[0,25 n - 0,5 arccos( -^ )]² -

1 + 0,25[0,25 n - 0,5 arccos( -^ )]²

1 - 0,0625[arccos( -H ) -n ]² _x

1 + 0,0625[arccos( -H ) - n ]²

0,25n- 0,5arccos(-H) | x-----------------—---7 ^;(8)

1 + 0,25[0,25 n - 0,5 arccos( -^ )]²

vjC) - vn I-----arccos( "

[ 4 + 0,25[arccos( -H ) - n ]²

x       0,5n - arccos(-H)

1 + 0,25[0,25 n - 0,5 arccos( -ц )]²

₊ 1 - 0,0625[arccos( -H ) - n ]² _x

1 + 0,0625[arccos( -H ) - n ]²

x 1z0125[G125n-015arccos(-H)]21

1 + 0,25[0,25 n - 0,5 arccos( -^ )]² J ^.

В области АВС линии скольжения также при- няты прямыми. Поэтому формулы (8) и (9) определяют скорость перемещения любой частицы в области АВС.

Совокупность формул (6)–(9) позволяет определить формоизменения металла в начальный момент процесса высадки концов труб.

Полученные зависимости применимы до тех пор, пока отсутствует препятствие течению металла по контактной поверхности. В реальных условиях процесса высадки концов труб скольжение по контактной поверхности ограничивается либо внутренней поверхностью матрицы, в которой осуществляются высадки, либо поверхностью пуансона, определяющего внутренний диаметр высаженной части трубы.

Расчеты по формулам (6)–(9) показывают, что в момент касания стенок матрицы или поверхности пуансона сетка линий скольжения и форма высаженного конца будут иметь вид, представленный на рис. 3.

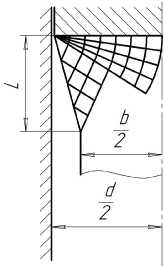
Рис. 3. Форма высаженного участка трубы и сетка линий скольжения в момент касания деформируемого металла стенки матрицы

Из рассмотрения геометрических соотноше- ний следует, что длина переходной зоны высадки L, изображенной на рис. 3, может быть определена по формуле

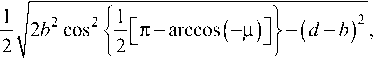
где d – зазор между пуансоном и матрицей.

Таким образом, теоретический анализ формоизменения при высадке концов труб показывает, что длина переходной зоны определяется толщиной стенки трубы b , величиной зазора между пуансоном и матрицей d и коэффициентом трения µ на контакте торца трубы и фланца пуансона.