Моделирование напряженно-деформированного состояния тонких композитных покрытий на основе решения плоской задачи градиентной теории упругости для слоя

В работе рассматривается задача о равновесии композитного бесконечного слоя, находящегося на жестком основании в рамках плоской постановки градиентной теории упругости. Исследование моделей градиентной теории упругости является одним из перспективных направлений развития современной механики [1-9]. Основной особенностью градиентных теорий является учет масштабных эффектов, которые могут быть связаны с материальным параметром или структурным параметром неоднородного материала. Этот параметр можно связывать и с протяженностью промежуточных межфазных зон в неоднородных материалах. Градиентные теории позволяют учесть нелокальные эффекты, обеспечивая более гладкий контакт различных фаз в окрестности границ за счет учета моментных факторов (бимоментных напряжений). В свою очередь, это приводит к повышению порядка разрешающих уравнений и переформулировке краевых задач в математической модели деформируемых сред. При решении практических задач градиентные модели оказываются эффективными для учета масштабных эффектов в материалах с характерным размером структуры, сопоставимым с протяженностью локальных градиентных полей. Примерами таких сред являются композиты с микро- и нановключениями, тонкослойные композитные покрытия, керамики с ультрадисперсной структурой и т.д. Такие материалы являются перспективными для применения в современной авиакосмической технике и требуют экспериментального и теоретического изучения. Задача, исследуемая в настоящей работе, связана с моделированием прочности элементов авиакосмических конструкций, на которые нанесены защитные композитные тонкослойные покрытия (керамические или металлокерамические).

Один из первых вариантов градиентной линейной теории упругости был предложен Тупиным [8]. В данной модели плотность потенциальной энергии изотропной среды может быть записана в виде

1U = С и и +D.., (1)

ijnm i, j n, m ijknmr i, jk n, ml, V / где Cijnm - модули упругости изотропного тела, j = Х5у5пт +

+ц ( 5 in 5 _jm +5 _jn 5 _im ); Х , ц - коэффициенты Ламе; 5 j - дельта Кронекера

(5j = 0, если i ^ j и 5ij = 1, если i = j); Dijknml - тензор модулей упругости, определяющий градиентные свойства среды (в общем случае для теории градиентной деформации градиентные свойства определяются двумя дополнительными параметрами, т.е. все компоненты тензора Dijknml характеризуются двумя модулями); ui - компоненты вектора перемещений, utj

д и ^д x j

и u j =

д ² U д x j д x_k

; принимается правило суммиро

вания по повторяющимся индексам, изменяющимся от 1 до 3.

Рассмотрим однородную область V , ограниченную поверхностью S . В отсутствие внешних сил лагранжиан, соответствующий деформированию рассматриваемого упругого тела, имеет вид L = — [ U d У . Найдем

г вариацию этого лагранжиана, используя интегрирование по частям.

Учитывая (1), получим

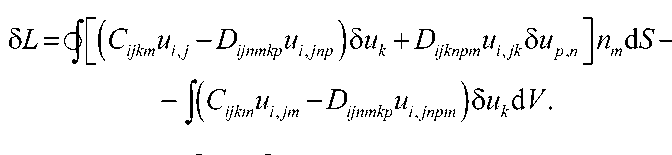
5L и •-D  uU ■ )5u, + D , u .JUи ijkm i, j       ijnmkp i,jnp )    k ijknpm i, jk    p,n

C-^u . — D , u .   15и,dV ijkm i, jm      ijnmkp i, jnpm J k

В выражении (2) 5 u_k , 5 u_pn являются вариациями вектора перемещений и вариациями градиента вектора перемещений соответственно; n - есть вектор внешней нормали к поверхности S . Равновесному состоянию рассматриваемой среды соответствует условие равенства нулю вариации лагранжиана (2), 5 L = 0. Учитывая (2), получим следующее уравнение Эйлера, являющееся уравнением равновесия рассматриваемой среды:

ijkm u i , jm      ijnmkp u i , jnpm

Уравнение обладает повышенными порядком по сравнению с классической теорией упругости. Для неоднородных сред с кусочнопостоянными свойствами уравнения Эйлера записываются отдельно для каждой из подобластей со своими тензорами модулей упругости C_iinm , D yknml • На поверхностях контакта подобластей I и II должны выполняться условия непрерывности, которые в данном случае имеют вид u i = Uj¹ и u | _k = u¹ ! . Для того чтобы выполнить условие 5 L = 0, в выражении для вариации лагранжиана (2) должны быть равны нулю статические множители, стоящие при 5 u_k и 5 u p _n на границе контакта подобластей:

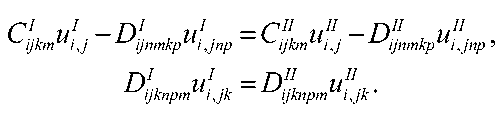
г u¹ _— п¹  U = г¹¹ u¹¹ _— п¹¹  u¹¹

jm'km^Ui , j   Jjynmkpi , jnp   Jijkuii , j   -Hynmkpi , jnp

D U = DI UI ijknpm u i, jk   ^-^ijlmpm u i, jk *

ций [10-11]. Для получения математической постановки модели рассмотрим лагранжиан модели типа модели Миндлина-Тупина:

^L = ^A - 2 Ul '

a R i a R_n s x j ^a x m

C     a2 Ri  a2 Rn ijknml axk axj axl axm

d V .

Введем гипотезы о пропорциональности когезионных модулей в (3):

C , - X C с , ijknml _C  ijrk^nmrl *

Таким образом, все многообразие когезионных свойств тел в рамках предлагаемой модели моделируется с помощью одного масштабного параметра C = р / l ². l - характерная длина, определяющая протяженность градиентных эффектов. В целом, модель определяет механические свойства сред с сохраняющимися полями дислокаций через четыре параметра среды: p , X , l .

Лагранжиан формулируемой теории приобретает вид

^L = ^А - 2 Hl C jnm

a R i a к_п ^a x j ^a x m

C ^ijrknmrmrl

a ² r a ² R_n a x_k a x j ax_t a x m

d V .

Вариационное уравнение, определяющее математическую поста новку модели, записывается в виде a 2(...)

⁵ L = W j " (

R r

- - C ,

C nmrl

R axlaxm J

+ РУ 5 R , d V +

i

i

+H P

5 R i d F -

—(

a ² R_n

rqnm axq axm

⁵ C^ p   d F = 0.

V       ^{a x}j J

Аналогичным образом может быть получена формулировка градиентной модели деформации, учитывающей адгезионные эффекты [12, 13].

2.    Постановка задачи о плоской деформации слоя в рамках градиентной теории упругости

Рассмотрим задачу о равновесии слоя, подверженного действию распределенный нормальной силы (рис. 1).

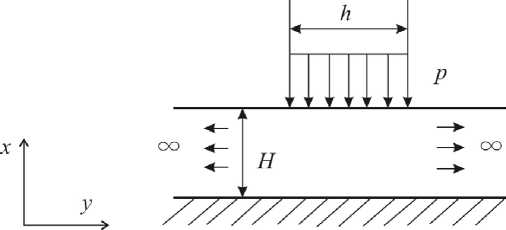
Рис. 1. К задаче о равновесии бесконечного слоя

Лагранжиан модели градиентной теории упругости в плоской постановке (плоская деформация) следует из общей формулировки модели (5) и имеет вид

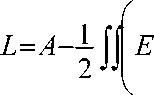
■ ^R/

₍ O x    O yy

+ G

^{a R} + ^K

(O y  O x

4 O R R'

O x O y

+

+

G ! l?M T c la y ² J (

^a x 7

+

R Y

(a x a y 7

f a ² R 1 2 _ ₂ a ² R a² r ₍a x a y 7 a x ² a x a y

2 R ^R J a y ² a x a y

+ E2.

C

'■ R

у ^a x ² 7

+& J (a y 7

+

f a ² r ,

- +

(a x a y 7 (a x a y 7

- + 2

a ² r , a² R 2 ₊ 2 a ² R 2 a ² r , a x ² a x a y a y ² a x a y

d x d y .

Вариационную постановку модели можно получить с помощью вариационного принципа Лагранжа, используя технику интегрирования по частям. Учтем, что модель следует записывать для бесконечного слоя (см. рис. 1), и поэтому из постановки будут исключены граничные условия на гранях, параллельных оси О х. Получаем следующую постановку плоской задачи градиентной теории упругости.

Уравнения равновесия

E 2 6 4 R _t G ² д ⁴ R 1 E ² + G ² а ⁴ R     а ² R

--у +---у +---;—;— E--;— с аx4   с ау4     с   аx2 ау2    аx2

g ^ R + E ² - G ² f s R +_^a4 ^R ^J- ( e _ g ) a R = о а у ²      с (а x 3 а у а x а у ³ )         а x а у

E ² а ⁴ R 2 g ² а ⁴ R 2 E ² + G ² а ⁴ r 2      а ² R

II E с а у ⁴    с а x ⁴ с а x 2 а у ²     а у у

G< R 2 + E ^{2 -} G² P R .+JL R LJ- ( E - G ) ^а А а x ²      с (а x 3 а у а x а у ³ )         а x 6 у

Граничные условия x = const:

E E	' а3 R 1 а 3 R 2	+ E 2 + G 2 а3 R i + E 2 - G2		а R F E	г а R 1 а R 2	а R + 2 G =
с	( а x 3 а у 3 J	с а x а у 2     с		а x2 а у	(а x а у )	а у
J G !	(а3 R 2 а 3 R 1 )	+ E 2 + G 2 а3 R 2 + E 2 - G 2		а3 R i Г G	' а R 1 а R 2	= о,
с	( а x 3 а у 3 J	с а x а у 2     с		а x2 а у	(а у а x )
E l	' а 2 R 1 + а 2 R 2	= о,    G 2	(а 2 R 2 а 2 R 1 )	= 0.
1 с	( а x 2 а x а у v	C	( а x 2 а x а у )

0,

Полученные уравнения равновесия соответствуют известному общему операторному представлению уравнений равновесия для моделей градиентной теории упругости, которое записывается в виде произведения оператора Ламе и оператора Гельмгольца:

LH ( R ) = 0,

Здесь L ( R ) = pV ² R + ( p+X ) V div R ; H ( R ) = R - L ( R )/ с ; R - вектор перемещений.

3.    Решение задачи о равновесии бесконечного слоя

Для решения задачи о равновесии бесконечного слоя применим интегральное преобразование Фурье:

Ri(x,у), R2(x,у)^Fi(x,го), F2(x,го), to

F( x, го)=;1 |*R1( x, у) e - iгоу dу, 2лЛ to

F 2 ( x , го ) = J R ( x , у ) e ^- i ^{го у} d у .

2л J

-да

В результате преобразования уравнения равновесия приводятся к следующему виду:

L 11 F + L 12 F 2 — 0,

L 21 F 1 + L 22 F 2 — 0.

Здесь введены следующие обозначения операторов:

L _— e ² a ⁴

¹¹ с a x ⁴

(E ^A GL _Ю 2 ₊ E J! + to 2 ( g ₊ G_ «Д

\ с           a xx ²      с с а

^L 12 ^— i to

L 21 — i to

E ² - G ² X 3 _- . с   ax³

e ² - g ² a ³ _ с    a x ³

(^{E G} to 2 + E - G XL

\ с              a xx

(^{E G} to 2 + E - G XL

\ с              a xx

_T _ g ² a ⁴ /e ²+ g ²-л. _r\a²          .e ² 2^

L_oo —--- —I------- to + G ——+ to E + to .

²² с ax ^{4 (} с           a ax^{2     (} с a

Преобразуем граничные условия модели:

E ² a ³ F с a x ³

E ² + G² 2 ^{a F}i _F ^a F i --------to-- E--- с      a x     a x

E ² C

i to ³ F ₂ +

E ² - G ²

C

i to

a ² f ₂ a x ²

- ( E - 2 G ) i to F₂ + K аФ

( E * ) 2

C

al - i to ³ Ф+

-'■'^Ф      0

a x J

G ^{2 a} 3 F 2 E ² + G² 2 ^a F 2

------to ---- с ax3     с     ax

₊ E ² - G g"

C

. a ² f i to —r a x ²

Gi to F 1

G LFk+^ito3 F + ax с 1

-—— a i to^^— 0, с       a x x

g ² a ² f g² ■ a f a FF о

——f-—ito—1 - в —2—0, с ax2   с   ax e2 a2f  e2 • af2   af  (E )  эф

^E --F+— i to—² - A —1+-—^а^ЕФ — 0

к с ax2   с   ax    ax    с

В случае наличия жесткого (в заделке) закрепления следует задавать следующие кинематические граничные условия:

R i —

a R 1 a x

— R 2

a^ — 0 a x

Для решения полученной системы уравнений (6) сведем его к уравнению восьмого порядка. Для этого введем потенциал ф ( x , to ) следующим образом:

F 2 =- L _ПФ, F = 2 ^ф.

Подставляя (8) в (7) получим, что первое уравнение равновесия удовлетворяется автоматически, а второе уравнение системы сводится к уравнению восьмого порядка относительно введенного потенциала:

L 11 А2 Ф + L ^" L ^) = ( L 11 L 12 - L 12 2 ^ = 0, ^L 21 ^L 12 ^ + ^L 22 ^{( -} А1 ф ) = ^L 21 ^L 12 ^^{- L} 22 А1 Ф = = ( L 21 L 12 - L 22 L ₁₁) ф = ( L ^ - L 22 L J - 0.

Полученное уравнение восьмого порядка имеет вид ( L - L 22 ДДф- 0.

Далее запишем данное операторное уравнение в координатной форме. Получаем

G ² E ² ^Ф , ----;г+ с с a x ⁸

+

E ² - G ²

C

•E ² - G ² •_ G ² f E ² + G ² i to----------- 1 to+ ----------

C C l C

to ² + E +

E ² + G ² m² p

------to + G l C

A

e ² la ⁶

Ф

7 с J a x ⁶

+

E ² - G ² —

C

i tof ^{E 2} C ^{G 2} i to ³ + ( E - G ) i to

EG i to 3 + ( E - G ) i to) EG i to- G f G ² to 4 + G to 2 с            7 с с l с

f E ² + G ² m² I F^f E ² + G ² m2 I f) f E ² _fn4 I 2 c E ) E ²

- -------to + G -------to + E - --to + E to -- a4^

⁺ a x ⁴

+

^{E 2 - G 2} i to ³ + ( E - G ) i to|| E²

C             7l

C

G ² i to ³ + ( E - G ) i to|+

, f E ² + G ² ,^2

+ ------to + G l C

—to ⁴ + G to ² |+| — to ⁴ + E to ² l с 7 l с

E ^+ G ² « 2 + E

C

E ² to ⁴ + E to 2

C

—to + G to |ф= 0.

, )la ² p

>Ja xx

Характеристическое уравнение выражения (9) содержит 4 корня второй кратности. Общий вид решения для потенциала может быть представлен в следующей форме:

/ C + G ю ²             i C + G ю ²           IC + G ю ²             IC + G to ²

. -----------x             —. -----------x             . -----------x             —. Ix

ф(x) = C1 e G  + C2e   G + C3e E  + C4e

+Ce юx + Cxe"юx + C7eюx + C.xeюx. 5   678

Это решение содержит в себе классическую часть - решение би-гармонического уравнения плоской задачи теории упругости (слагаемые с коэффициентами С5...С8). Запишем далее в операторной форме систему граничных условий. После преобразования Фурье имеем:

E ² 6 3 . E ² + G 6

E -⁶-

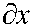
F +

---7 +--ю —

C 6 x ³     C     6 x

+

+

—i ю C

— E'¹' ( i ю ) ⁶ + ( E — 2 G )( i ю ) C      6 x

GL i ю 3 — EZ^GL ( i ю )

CC

G ² 6 3 . E ² + G _{( >}

---7+-- ю

C 6 x ³     C

—( i ю) — F +

C    ^xx J 1

. EE-6x ²

. 2 6

6 x

G ² 6 ²

_ C 6 x

F 2 = 0,

^{1 G (} i ^{ю ) F} 1 ⁺

^{+ G} К j ^F 2 ^{= 0}’ ■ ^B l x ] ^F 2 * ⁰’

E ² 6 ² _— . C 6x x

A ⁶L 6 x j

F + E ²( i ю ) E- F, = 0.

¹ L c     6 x J ²

Подставим в данной системе выражения для трансформант функций перемещений через введенный потенциал. Получаем l =- EL8 J EL±GL to2 + E 5L, 31 C 8x3 \ C

L 32 = C i to ³ - ECG ( i to ) 8L + ( E - 2 G )( i to ),

L ₄₁ = - ^{E - G} ( i to ) -⁵-:-+ G ( i to ) - —i to ³,

41 C      'xx2

G2 83 , /E2 + G2 2 ,

+         to + G ,

C 8x3 \ C

L 42

^L 51

L 61

G- ( i to ) ^, L ₅₂ = G 4 - B ^, C    ^xx   ⁵²    C 8 x ²     8 x

E ² 8 ²

C 8 x ²

A , l₆₂=EL _WLL.

8 x      C     8 x

Подстановка общего вида решения для введенного функционала в полученную систему граничных условий (с учетом дополнительных граничных условий в заделке) позволяет найти все неизвестные коэффициенты С 1... С 8. По потенциалу могут быть найдены трансформанты перемещений F 1 и F ₂. Далее требуется взять обратное преобразование Фурье для определения функций перемещений, возникающих в слое:

ю

ю

u ( x , у ) =— [ F ( x , to ) e i ^to x d to ; v ( x , y ) =— [ F ₂( x , to ) e i ^to x d to . 2л ^J                          2л ^J

-ю

-ю

При проведении численного моделирования это интегрирование проводилось численно, так как аналитическое решение для оригиналов не удается получить в короткой и удобной для вычислений форме. При этом проводился анализ сходимости процедуры численного вычисления обратного преобразования Фурье. Показана сходимость численной процедуры как при измельчении шага интегрирования, так и при увеличении интервала интегрирования (несобственный интеграл приближенно вычислялся на ограниченном интервале, с учетом условий затухания решения).

Возникающие в слое деформации определялись из классических соотношений Коши, которые остаются справедливыми и для градиентной модели [10]:

_{р =} ди _Р   d v _Р

Ь11    ~ , ъ22   ~ , ъ дx      ду

' 12

_ 1 f д и ! д v

Л

2 ^д у д x _v

.

Представление для полных напряжений в плоской задаче градиентной модели может быть получено из формул Грина, примененных к плотности потенциальной энергии деформаций. Эти напряжения по своей записи совпадают с представлением напряжений для классической задачи теории упругости в плоской постановке:

^ст x ^_ 2 ц

v

_ 1 - 2 v

( 9 1 + e ) +

д и

д x _ ,

ст у ^_ 2 ц

^v ( 9 + e ) ₊S v , 1 - 2 v ¹       д у _

^т xy ^_Ц

д и + 5 v _ду д x _

^ст _z ^_ 2 Ц

v

_ 1 - 2 v

9+ -ЬУ- e ¹ 1-2v .

Здесь

9 -5 u .+5 v _ l - 2 v ( ст +ст ) - 2 v e.

1          xy дx ду 2ц

• 4.    Моделирование двухслойного композитного покрытия

С точки зрения приложений и практического применения результатов моделирования представляется интересным рассмотрение задачи для двухслойного покрытия. В этом случае имеем два потенциала перемещений в каждом из рассматриваемых слоев, общий вид которых следующий:

IC + G to ²              IC + G to ²

1x             -

Ф 1 ( x ) _ A 1 e   G ¹    + A ₂ e ’ G ¹

C + G to ²             C + G to ²

11x -.

+ A3 e-  E1   + A4 e    E1+

+Ae-tox + Axe-tox + Aetox + Axetox. 5   678

IC, + G , to ²                ! C, + G , to ²              ! C, + G , to ²                ! C, + G , to ²

А —--2--x       - —--2--x        —--2--x       - —--2

ф2(x) _B1 e  G2   + B2e '  G2   + B3e’  E2   + B4e    E2

+Be tox + B6xe"tox + B7etox + B.xetox. 5   678

Граничные условия модели при заданной распределенной силе (через функции Хэвисайда) имеют вид

⁽ w w

La i [ ф ! ( x ) , Ф 2 ( x ) J x 0 = ----------- , La 2 [ Ф 1 ( x ) , Ф 2 ( x ) J x = 0 = 0,

< La 3 [ ф 1 ( x ) , Ф 2 ( x ) ] x 0 = 0, [ Ф 1 ⁽ x ⁾ , Ф 2 ⁽ x И x = h + H = ⁰.

^Lb 3 [ Ф 1 ⁽ x ) . Ф 2 ⁽ x ⁾ ] x . h + H = ⁰

La 4 [ ф 1 ( ^x ) . Ф 2 ( x ) ] x = 0 = ⁰ Lb 2 [ ф 1 ⁽ x ⁾ , Ф 2 ^{( x )} ] x = h + H = ⁰, Lb 4 [ ф 1 ⁽ x ⁾ , Ф 2 ^{( x} ) ] x = h x H = 0.

Контактные условия

Ф 11 ( x ) =Ф 21 ( x )| x = h , Ф 12 ( x ) = Ф 22 ( x )| x = h ,

71TФ 11 ' ( ^{x )}= 777 Ф 21Ч ^{x )}    ,

C ₁          C ₂

x = h

Фи( x ) = Ф 21 ' ( x

22 EE 777 Ф 12 ^{( x )}= 727 C ₁          C ₂

( x )   Фз'( x ) = Ф22'( x )   ,

x = h

x = h

Ф 22" ( x )    ,

x = h

E ²

^ 1 Ф 11 ^, ( ^x ) - 772 Ф 11" ( ^x ) = ^£ 2 Ф 21 ' ( ^x )

C ₁

E ттг Ф21 (x), C2

E ²

ДФ 12 ' ( x ) --^2Ф 12^ ( ^x ) = ^Е2 Ф 2^ ( x )

C ₁

Т7ГФ22 ^{( x )} -

C ₂

В приведенной постановке использованы обозначения

<

La 1 =

+

E 1 ²

La ₂ =

+

E ^ ²    +

C _i a x ³

C 1

f E i ² + G 1 ²

V

C 1

^ ro + - 1

a a x

F i +

G ²      2

—— i ro-^7

a x ²

- i² -

C 1

G ²

—— l ro

f                     ^

+ E^ i ro ³ + ( - i - 2 G i ) i ro F2,

V C i                    7_

F i +

a ² a x ²

+ G_ii ro

V

G ²

—— i ro ³

C 1

G i ² aL. +

C 1 a x ³

La 3 =

G

f E i ² + G 1 ²

A

V

a

C 1

^ro 2 ^{+ G} i 7" ^F2 , a x

La ₄ =

V Ci f EL aL

V c _i a x ²

1- iro^- F i +

a x _v

7 ^f GL aL. V C 1 a x ²

в ar F 2 ’ a x j

^    f F2     ^

A 7- F + - ¹- i roT- F .

a x _v

V C i    ^a x j

Lb₁ =

+

- 22 5 3

C ₂ 5 x ³

+

e₂ ² - G ².

——— i to

C 2

Lb ₂ =

+

Lb ₃

Lb 4

Г

V

E ² + G²

—----— to² + E,

C ₂

5² 5 x ²

+

E ² - G ₂² .

—---— i to

G dL C ₂ 5x ³

C 2

+

Г

V

А

5 x

F +

E ²                  7

i to ³ + ( E 2 - 2 G 2 ) i to F 2 ,

C 2                     j_

5 x ²

+ G₂i to V

E ₂ ² + G ₂ ²

G ² Л 1-- — i to ³

C 2    J

A _

F +

V 2

to ² + G 2 f F 2 , 5 x

f G 2 ²

V C 2

A

i to'    F +

5 x ₇

f G ■

V C ₂ 5 x x

B $ 5 x ₇

^F 2 ^,

f E 2L 5L

V C 2 5 x x

A

A   F i +

f E 2 ²

A

5 x ₇

i to-⁵- F ₂.

V c 2    5 x j

Граничные и контактные условия образуют линейную систему из 16 уравнений с 16 переменными; решая систему, находим постоянные A i^_{ = ₁ ^ 8 ) , B i ( i = ₁ ^ 8 ) и путем численного обратного интегрального преобразования Фурье находим перемещения в слоях, и далее по формулам (10) и (11) находим деформации и напряжения.

5.    Результаты численных вычислений

Задача о равновесии слоя, находящегося на жестком основании под действием нормальной силы, решалась на основе алгоритма, изложенного в предыдущем пункте с использованием системы символьных вычислений Mathematica. Для тестовых вычислений были взяты следующие параметры модели: модуль упругости Е = 1, модуль сдвига G = 0,35, градиентный параметр и толщина слоя задавались переменными. Ширина площадки действия силы задавалась единичной. На рис. 2 представлен характер распределения перемещений в направлении осей X и Y по толщине слоя.

Получаемое численное решение соответствует физическому смыслу задачи: наибольшие перемещения возникают в области приложения нагрузки, решение затухает на бесконечности, и в заделке перемещения отсутствуют. Деформации и напряжения, возникающие в слое, представлены на рис. 3 и 4.

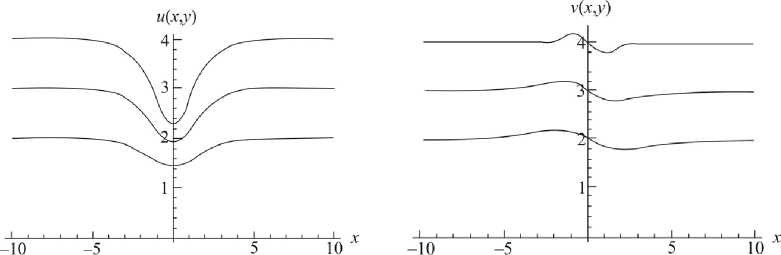
Рис. 2. Распределение перемещений по толщине слоя при действии нормальной силы

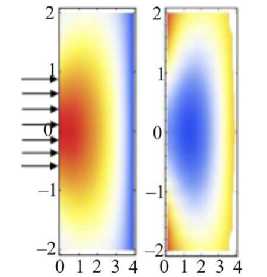
Рис. 3. Компоненты тензора деформаций 11 и 22, возникающие в слое под действием нормальной силы в градиентной модели

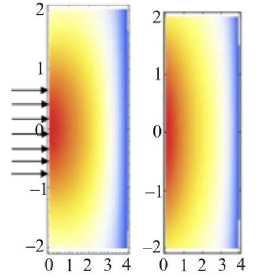
Рис. 4. Компоненты тензора напряжений 11 и 22, возникающие в слое под действием нормальной силы в градиентной модели

6.    Зависимость НДС от толщины слоя и градиентного параметра

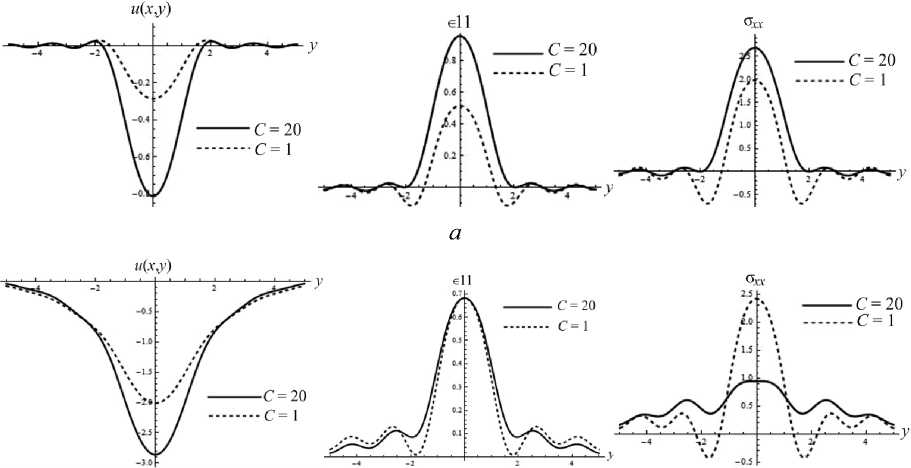
В рамках градиентной модели представляется важным исследование зависимости НДС покрытий различной толщины. Модель учитывает масштабный градиентный параметр l ( С ), характеризующий протяженность когезионных взаимодействий. Учет градиентных эффектов особенно интересен в области границ контакта. Для тестовых значений механических параметров задачи было исследовано изменение перемещений, напряжений и деформаций при изменении толщины покрытия в 5 раз. На рис. 5 показан характер изменения перемещений, деформаций и напряжений на верхней границе покрытия при увеличении толщины слоя (или при уменьшении градиентного). Видно, что максимальные нормальные перемещения увеличиваются для покрытий большей толщины. При этом для тонких покрытий уровень напряжений возрастает в 3 раза.

б

Рис. 5. Характер изменения нормальных перемещений, деформаций и напряжений на верхней границе покрытия при увеличении толщины слоя: а - h = 1 мкм; б - h = 5 мкм

а

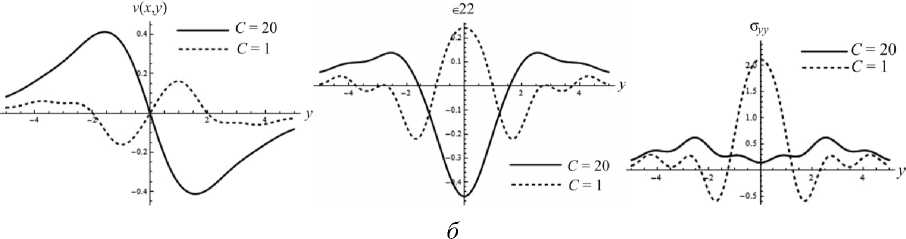
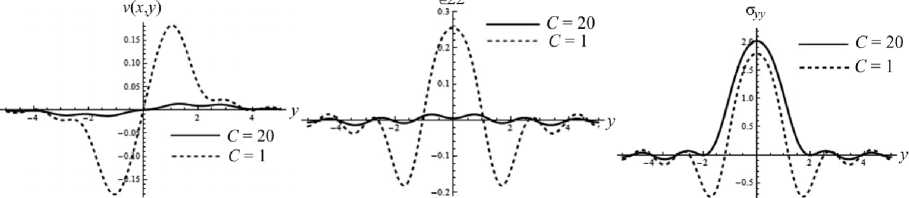
Рис. 6. Характер изменения перемещений, деформаций и напряжений в плоскости на верхней границе покрытия при увеличении толщины слоя: а - h = 1 мкм; б - h = 5 мкм

На рис. 6 показано, что при изменении масштабных параметров перемещения, деформации и напряжения в покрытии, в плоскости слоя, могут изменять знак. Таким образом, учет градиентных эффектов может кардинальным образом менять картину напряженно-деформированного состояния тонкослойных структур.

7.    Моделирование двухслойного покрытия

Для численного моделирования двухслойного покрытия было принято, что свойства подложки в десять раз отличаются от свойства верхнего слоя покрытия: Е ₁/ Е ₂ = 0,1, G ₁/ G ₂ = 0,1. Перемещения, возникающие в двухслойном покрытии под действием распределенной силы на площадке шириной {-1,1}, представлены на рис. 7.

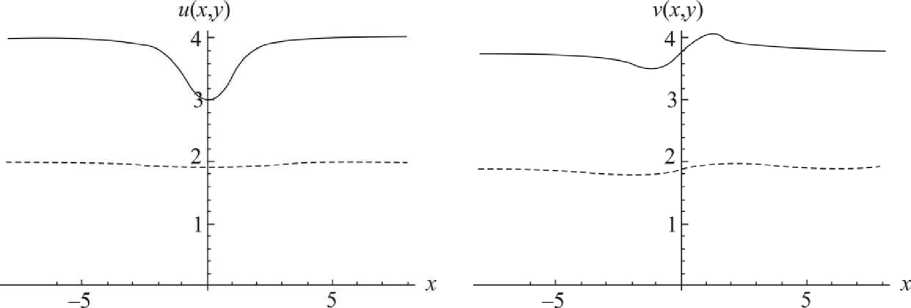
Рис. 7. Перемещения в подложке (пунктир) и в верхнем слое (сплошная линия) покрытия, возникающие под действием распределенной силы

На рис. 8 представлены соответствующие напряжения и деформации, возникающие в двухслойной задаче.

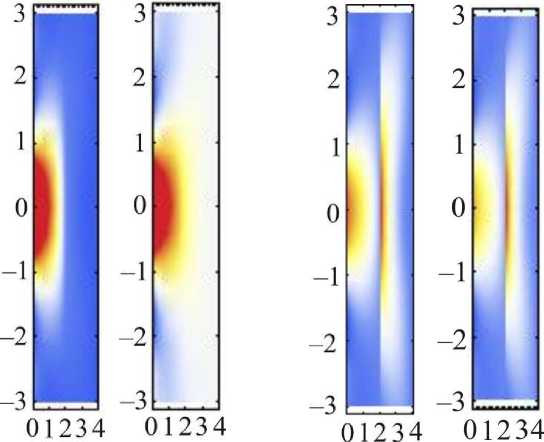
£ 1 , £ ₂                          ^ 1 , ^

Рис. 8. Деформации и напряжения, возникающие в двухслойном покрытии под действием силы

Из рис. 8 видно, что основная концентрация деформаций и напряжений происходит в более мягком поверхностном слое, однако на границе двух материалов возникает дополнительная концентрация напряжений, связанная с различием коэффициентов Пуассона материалов и влиянием градиентных эффектов.

Заключение

В работе исследована плоская задача градиентной теории упругости. Построено численное решение задачи о равновесии бесконечного композитного слоя, находящегося на жестком основании, при действии распределенной нормальной силы. Решение задачи проводилось с использованием интегрального преобразования Фурье, однако для вычисления обратного преобразования потребовалась реализация алгоритма численных вычислений. Исследована зависимость напряженно-деформированного состояния композитного слоя в зависимости от толщины слоев и градиентного параметра модели. Прикладное значение решенной задачи связано с возможностью достоверного моделирования и оптимизации микроструктурного строения ультратонких защитных композитных покрытий, применяемых в различных отраслях промышленности.

Работа выполнена при поддержке РФФИ, проект №12-01-00273-а, №12-01-31220/12 и ФЦП «Научные и научно-педагогические кадры инновационной России на 2009-2013 г.», ГК № 14.740.11.0995, соглашение №8221 и соглашение №14.В3 7.21.2060.