Моделирование неадамаровского квантового блуждания для решеток высших размерностей

Модель квантового случайного блуждания активно изучается в последнее десятилетие в связи с возможным применением ее результатов в теории квантовых вычислений и ускорении алгоритмов, основанных на случайном блуждании. Более того, указанная модель имеет неожиданные приложения в теории прямых и обратных задач рассеяния [1].

Одномерное квантовое случайное блуждание. Прежде чем определить дискретное квантовое блуждание, опишем классический случай [2]. Симметричное классическое блуждание может быть реализовано следующим образом. Частица начинает движение, например, из начала координат, на каждом шагу подбрасывая монетку, она равновероятно выбирает направление движения. Затем она делает один шаг в выбранном направлении и т. д.

В более общем случае, когда частица выбирает направление не равновероятно, а с вероятностями p и q = 1 - p , вероятность нахождения классической блуждающей частицы в момент времени t + 1 в ячейке с номером n выглядит следующим образом:

P ( t + 1) = pP +1( t ) + qP -1( t ). (1)

Y ( n , t + 1) =

f 0

V N 2

0 ) --1 V 2 J

Y ( n - 1, t ) +

f 1

V2

V 0

1'

V2 Y ( n + 1, t ) = 0 J

= M _ ^ ( n - 1, t ) + M Д n + 1, t ).

Вероятность нахождения квантовой частицы в узле с номером n в момент времени t выражается следующей формулой:

P ( n , t ) = | v l ( n , t )|² +1 v r ( n , t )|².

Если частица начинает свое движение из начала

координат с исходным состоянием «влево», то начальные условия будут выглядеть следующим образом:

^ (0,0) = 1 ₀ I , ^ ( n ,0) = 1 ₀ I , n * 0,

Тем самым, задав распределение вероятностей нахождения классической блуждающей частицы в начальный момент времени, можно вычислить распределение вероятностей для любого наперед заданного момента времени t .

Квантовое обобщение случайного блуждания [3] рассматривает квантовую частицу, обладающую дополнительной степенью свободы, и характеризуется двукомпонентной волновой функцией

и адамаровское квантовое случайное блуждание станет сводиться к решению двумерной системы уравнений в конечных разностях.

В общем случае характеристики квантового случайного блуждания (унитарного преобразования над волновой функцией) зависят от четырех параметров. Однако, как было отмечено в [3], достаточно рассмотреть зависимость от одного параметра, характеризующего семейства блужданий. Таким образом, общее случайное блуждание может быть описано следующим преобразованием:

^ ( n , t ) =

V L ⁽ n , t )

V R ( n , t )

M ( 9 ) = T ° ( I ® U ₆), где U ₉ = e ⁹” y .

Оператор M ( 9 ) описывает эволюцию блуждания:

T ( t + 1) = M ( 9 ) ^ ( t ). Адамаровское случайное блуждание соответствует значению параметра 9 = п / 2:

амплитуд в ячейке с номером n во время t . Поведение во времени функции T ( n , t ) задается унитарным преобразованием.

Определение 1. Адамаровское случайное блуждание – это случайное блуждание, задаваемое правилом

f 1       1 )

1 f l 1 )=_/ -■   ⁰V2 V2

V2 V1 -1J    V0 -1J - _L _L

V Л V2 J

i ^п^

-e ²zU п,

где дополнительное вращение может быть нивелировано подходящим переопределением фазы состояния.

*Работа поддержана Российским фондом фундаментальных исследований (грант № 08-01-00312).

В более удобном для использования виде эволюция квантового блуждания может быть записана как

( о

V ( n , t + 1) =

+

к

к

А cos

sin ⁰

—

0 1

о V ( n — 1, t ) + cos⁰

2 7

Sin ⁰

2 ^ ( n + 1, t ).

0 7

Используя выражение для волновой функции (2), можно вычислить распределение вероятностей нахождения квантовой частицы для различных начальных состояний частицы и различных значений параметра 0 .

Результаты расчетов для вероятности возвращения квантовой частицы даже для не очень большого числа шагов, приведенные на рис. 1, позволяют сделать вывод, что распределение вероятностей нахождения квантовой частицы в заданной точке достаточно сильно зависит как от начального состояния частицы, так и от параметра 0.

Здесь и далее нас будет интересовать такая характеристика, как вероятность возвращения квантовой блуждающей частицы в исходную точку за t шагов по времени, а также асимптотические свойства этой характеристики. Интерес к данному показателю обусловлен связью вероятности возвращения и свойства локализации [1].

Возвратные марковские цепи. Локализация в модели квантового блуждания. В теории классических цепей Маркова большое внимание уделяется возвратным состояниям. Рассмотрим цепь Маркова { Xn } ”=о- Если в n -м испытании реализовалось событие Ej , то будем считать, что X_n = j . Введем следующие обозначения:

fj (n) = P(Xn = j,Xn—, * j,...,X, * j | Xо = j), да

Fj = L fj( n ).

n =0

По аналогии с вышеприведенными рассуждениями и определением локализации в моделях, рассматриваемых в [4], можно определить следующие понятия.

Определение 3. Квантовое случайное блуждание называется локализованным, если lim pr. (n) > 0, где n ^да pr (n) = P(0, n) - вероятность возвращения квантовой частицы в начальную точку за n шагов.

Определение 4. Квантовое случайное блуждание да называется слабо локализованным, если ^ pr (n) = да. n=0

Свойство возвратности одномерного квантового блуждания достаточно подробно описано в работе [1] и представлено следующей теоремой.

Теорема 3 (одномерная квантовая теорема Пойа). Пусть 0 = 0, тогда квантовое блуждание на прямой с любым начальным состоянием не возвратно. Пусть 0 < 0 < п , тогда квантовое блуждание на прямой с любым начальным состоянием возвратно (слабо локализовано). При этом главный член асимптотики не зависит от начального состояния. Пусть 0 = п , тогда квантовое блуждание на прямой с любым начальным состоянием возвратно (слабо локализовано). При этом P ₀ ( n , t ) = 0 при | n | > 2.

Квантовое случайное блуждание высших размерностей. Одномерное классическое блуждание на прямой описывается эволюционным уравнением для вероятности нахождения в точках с целыми координатами (1). Аналогичное уравнение, но уже зависящее от четырех параметров, имеет место для классического блуждания по точкам с целыми координатами на плоскости (а в общем случае – и для блуждания по точкам с целыми координатами в пространстве размерности n ):

^Px , y ⁽ t ⁺ 1) = p 1 ^Px +1, y ⁽ t ) ⁺ p 2 ^Px —1, y ⁽ t ) ⁺

⁺ p 3 ^Px , y +1⁽ t ) ⁺ p 4 ^Px , y —1⁽ t ).

Определение 2. Состояние E_j называется возвратным , если Fj = 1, и невозвратным , если Fj <  1.

Пусть pj = P ( X_k = j | X ₀ = i ). Важным способом проверки возвратности является следующая теорема [2].

Теорема 1. Состояние Ej возвратно тогда и толь- да ко тогда, когда ^ pjj = да.

j =1

Численно исследуя асимптотические свойства убывания членов ряда p_jj , можно cделать выводы о его сходимости или расходимости, а следовательно, и выводы о возвратности цепи Маркова.

В случае классического случайного блуждания имеет место следующая теорема [2].

Теорема 2. Описанное случайное блуждание образует возвратную цепь Маркова тогда и только тогда, когда p = q = 2.

Вероятности p_i соответствуют вероятности классической частицы совершить шаг вправо, влево, вверх и вниз. Для квантового случайного блуждания роль вероятностей играют матрицы P = M ₊ и Q = M _—.

Соответствующее уравнение для амплитуд вероятностей выглядит следующим образом:

V ( n , t + 1) = P V ( n + 1, t ) + Q V ( n — 1, t ).

Множество начальных состояний квантовой частицы имеет вид

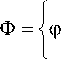
a в

e C ² :| a |² + | в |² = 1

Матрица преобразования для одномерного адама-ровского блуждания будет такой:

h = i I1

— 1

0.3
-10	-Б	5	10
	0.3
	0.2S
	0.2
	0.15
	0.1
	0.05
-30	-ВО        -10	10         20	30

	0.35
	0.3
	025
	02
	0 15
	0.1
	0.05
-20	-10               15	10               20
	0.25
	02
	0.15
	0.1
	0.05
—40              -20              и		20               40

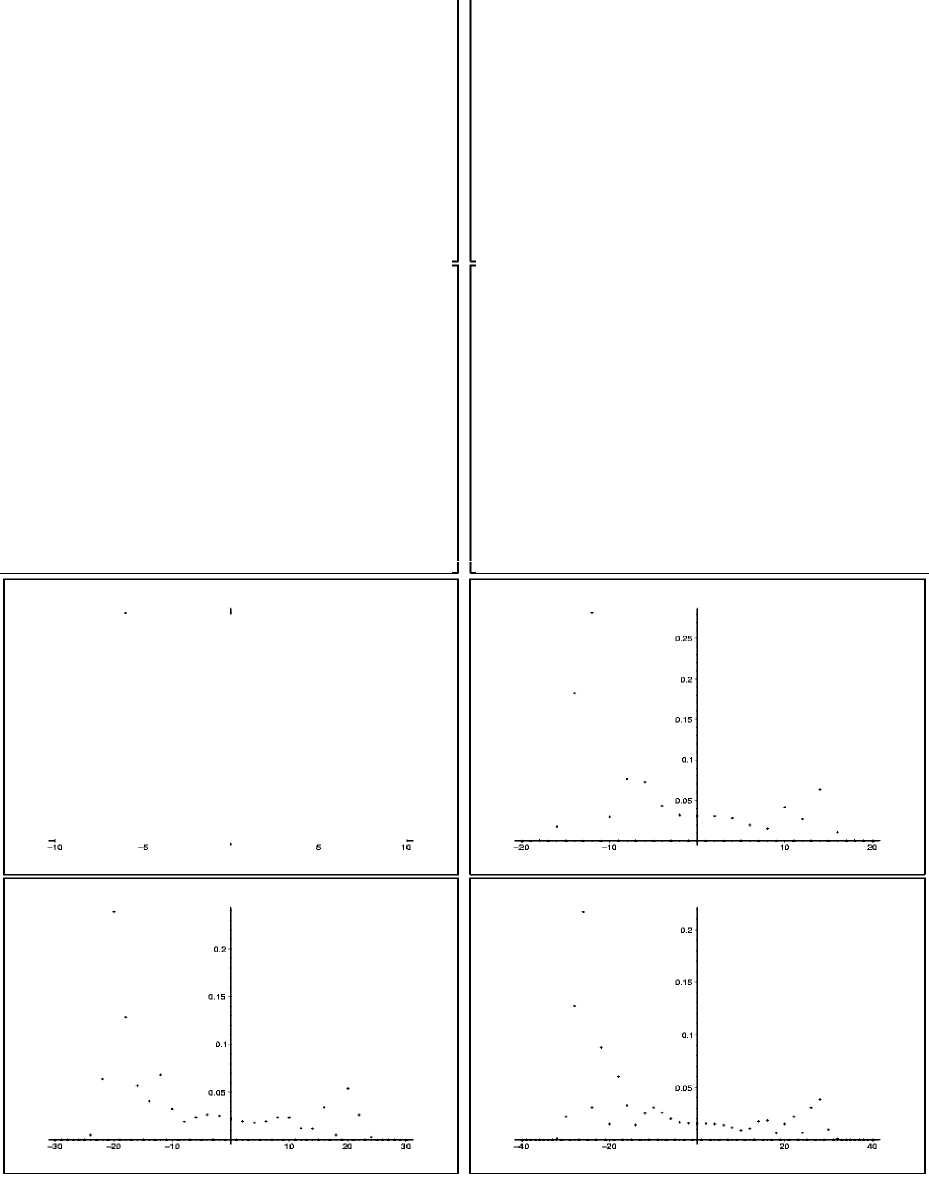
Рис. 1. Распределение вероятностей возвращения для блуждающей квантовой частицы:

Г )

.     0 1
-10              —5	5                    10

верхние четыре рисунка - 9 = ^^З, ¥ (0,0) =

2 i

, число шагов по времени 50, 100, 150, 200;

k V2 7

нижние четыре рисунка - 9 = П , ^ (0,0) =    , число шагов по времени 50, 100, 150, 200

²                 ( 0 )

Обобщение квантового случайного блуждания на многомерный случай определяется матрицами большей размерности [5]:

H = h ® h ® ® h , dd

являющимися тензорным произведением матриц одномерного случайного блуждания. В этом случае множество начальных состояний квантовой частицы выглядит как

Ф ⁽ d ) = { ф 1 ®ф ₂ 0... 0ф d : ф , €Ф , i = 1,2, ^ , d }.

Определение 5. Двумерным адамаровским случайным блужданием называется блуждание, описываемое матрицей

	( 1	1	1	1 )
1	1	- 1	1	- 1
H = H = H ® H = -
H1     2	1	1	- 1	- 1
	1 1	- 1	- 1	1 7

Вероятность нахождения квантовой частицы в соответствующем узле ( n , m ) определяется аналогично одномерному случаю:

P (( n , m ), t ) = 1 ^ i (( n , m ), t ) |² + | Y 2(( n , m ), t ) |² +

+ I Y 3 (( n , m ), t ) |² + 1 Y 4 (( n , m ), t ) |².

Другим примером двумерного квантового блуждания является блуждание, описываемое матрицами H ₂ (Гровера) и H ₃ :

H 2

(-1

1 1

2 1

- 1

- 1

1)(

11-11

1 • H■ = 2-11

1    1 )

- 1   1

- 1

- 1

- 1

- 1

Как и раньше, нас будет интересовать такая характеристика блуждания, как вероятность возвращения в исходную точку за определенное число шагов, например за 20 (рис. 2).

Сложность изучения квантового случайного блуждания обусловливается еще большим числом все

возможных конфигураций и степеней свободы по сравнению с блужданием на одномерной решетке (см. рис. 2).

Проследить асимптотические свойства вероятности возвращения в исходную точку можно на рис. 3, где изображены результаты компьютерного моделирования. Эти результаты показывают, что вероятность возвращения для блуждания с матрицами H ₁ и H ₃ убывает на бесконечности как 1 t ² и, следовательно, невозвратно.

Особенно интересным в качестве объекта численного исследования является случайное блуждание Гровера, которое имеет принципиально иной асимптотический характер вероятности возвращения в исходную точку (пропорционально t ⁰ ).

Таким образом, результаты моделирования позволяют сформулировать следующие гипотезы.

Гипотеза 1. Асимптотика вероятности возвращения квантовой частицы в начало координат не зависит от начальных условий.

Гипотеза 2. Подмножество параметров квантового блуждания, при котором оно обладает свойством возвратности при любых начальных данных, имеет меру нуль.