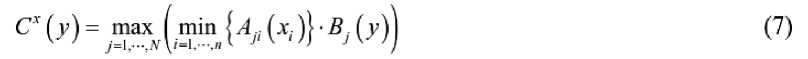Моделирование нечеткой логики для управления процессом бактериального окисления концентратов в реакторах с мешалкой
Автор: Г.Б. Махмудов, А.Х. Саидова, Н.Т. Мохилова
Журнал: Современные инновации, системы и технологии.
Рубрика: Управление, вычислительная техника и информатика
Статья в выпуске: 2 (2), 2022 года.
Бесплатный доступ
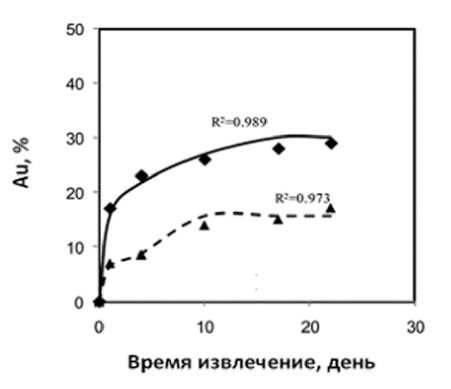
Множественность химических, биологических, технологических параметров и нелинейная зависимость при извлечении металлов в средах бактериального окисления усложняют математическое моделирование этих систем. Данное исследование было проведено с целью обеспечить управление извлечением золота и железа из флотоконцентрата в биореакторе с мешалкой с использованием модели нечеткой логики. Опыты проводились в присутствии смешанной культуры ацидофильных бактерий (Lactobacillus acidophilus) при 42°С и смешанной культуры умеренно термофильных бактерий при 48°С. Входными переменными были: метод операции, тип бактерий и время. Извлеченное золото и железо являлись выходными данными. Связь между указанными входными данными и выходными данными была обеспечена с помощью разработанных правил «ЕСЛИ-ТО». Полученная нечеткая модель показала удовлетворительный прогноз извлечения золота и железа и имела хорошую корреляцию экспериментальных данных с R-квадратом (более 0,97). Результаты исследования показали, что нечеткая логика представляет собой мощный и надежный инструмент для прогнозирования нелинейных и изменяющихся во времени процессов бактериального окисления.
Нечеткая логика, моделирование, флотоконцентрат, бактериального окисления, реактор с мешалкой
Короткий адрес: https://sciup.org/14123387
IDR: 14123387 | DOI: 10.47813/2782-2818-2022-2-2-0201-0214
Текст статьи Моделирование нечеткой логики для управления процессом бактериального окисления концентратов в реакторах с мешалкой
Традиционное или химическое бактериальное окисление золота из концентратов в реакторах с мешалкой является одним из самых сложных и трудоемких процессов в гидрометаллургии. Процесс не только не линеен и изменчив во времени, но и трудно детерминирован. Процесс бактериального окисления состоит из двух взаимодействующих подсистем: абиотической системы, представляющей собой минеральную взвесь в растворе химических соединений, и биологической системы, состоящей из единичной или смешанной культуры микроорганизмов. Для математического моделирования этого процесса необходимо учитывать слишком сложный массоперенос между тремя разными фазами [1]. С другой стороны, наличие нескольких видов ацидофильных бактерий, имеющих разные механизмы растворения минералов, усложняет природу биологической подсистемы. Таким образом, систему не только сложно описать математически, но еще труднее обосновать экспериментально из-за чрезмерного упрощения условий, вследствие чего протекание процесса нельзя точно запрограммировать.
Использование нечеткой логики, отражающей качественный и неточный характер человеческого мышления, может сделать экспертные системы более гибкими [2]. Данные исследования были инициированы в 1965 г. Лотфи А. Заде [3]. В модели нечеткой логики лингвистические переменные используются для передачи понятий, относящихся к компонентам системы, а лингвистические операторы используются для передачи понятий, связанных с взаимосвязью и динамикой этих компонентов. Системы нечеткой логики широко используются для задач управления, идентификации систем и распознавания образов. Основное преимущество нечеткой логики по отношению к традиционным математическим моделям заключается в том, что связь между входами и выходами определяется не сложными уравнениями, а набором логических правил, отражающих знания эксперта [4]. В сложных системах управления технологическими процессами нечеткая логика интегрируется с обычными ПИД-регуляторами и является очень полезным подходом к автоматизации процессов [5]. Нечеткую логику можно использовать для удобного включения практических внутренних знаний в решение по управлению [6]. В течение последнего десятилетия исследователи пытались прогнозировать как физическую, так и химическую переработку руд и концентратов, используя системы нечеткой логики [7-10]. Процесс бактериального окисления также моделировался различными методами [11]. Ранее была опубликована реакционная кинетическая модель традиционного и электрохимического бактериального окисления флотоконцентратов [13].
Учитывая множество различных химических, биологических, технологических и эксплуатационных параметров, нелинейное поведение извлечения металлов в процессах бактериального окисления и высокую способность систем, основанных на знаниях, в таких сложных средах, нами в этом исследовании использовалась нечеткая логическая модель с несколькими входами и многими выходами. Модель построена для управления процессом извлечения золота и железа из флотационного концентрата в биореакторе с мешалкой. Предложенная модель успешно предсказывает нелинейное поведение обычных и электрохимических процессов бактериального окисления.
ЭКСПЕРИМЕНТАЛЬНЫЕ ДАННЫЕ
Данные, используемые в представленном нечетком логическом моделировании, были получены из экспериментальной работы, выполненной ранее автором и его сотрудниками [14]. В данном исследовании сульфидный концентрат из рудника Кокпатас (Учкудук, Узбекистан) использовался для проведения традиционных и химических процессов бактериального окисления. Эксперименты проводились в шести модульном биореакторе при содержании твердого вещества 10% (масса/объем). Использовали смешанную культуру ацидофильных бактерий и смешанную культуру умеренно термофильных бактерий при 40°С и 48°С соответственно. Опыты проводили в питательной среде, скорость перемешивания 450 об/мин, приложенный потенциал 520 мВ, исходный рН 1,2-1,8, скорость аэрации 1,3 л/мин. Потенциал рабочего электрода контролировали относительно электрода сравнения с помощью измерительного прибора SIM 290. Детали используемого оборудования и методов были описаны ранее [15].
МОДЕЛИРОВАНИЕ НЕЧЕТКОЙ ЛОГИКИ
Система нечеткой логики представляет собой нелинейное отображение вектора входных данных в скалярный выход. Содержит четыре компонента: фаззификатор, базу правил, механизм вывода и дефаззификатор. В этом исследовании процесс нечеткого моделирования поддерживался Fuzzy Logic Toolbox программного обеспечения MATLAB. Стандартный метод создания модели можно увидеть на рисунке 1.
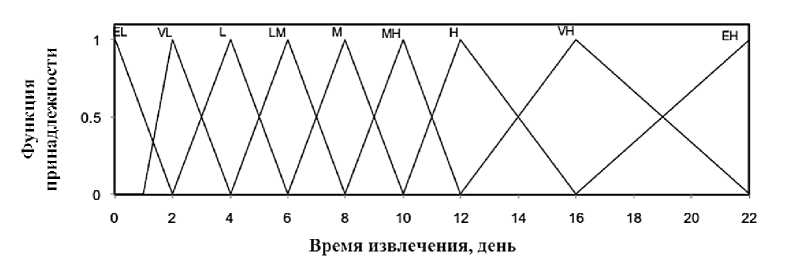
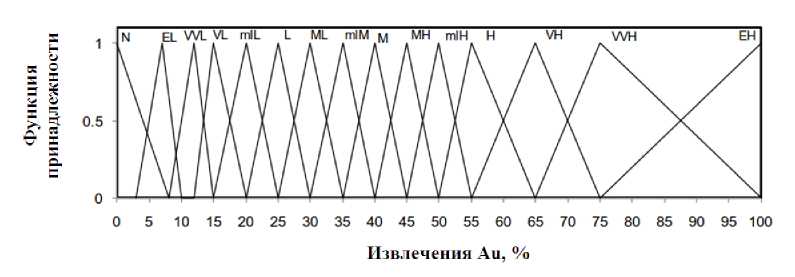
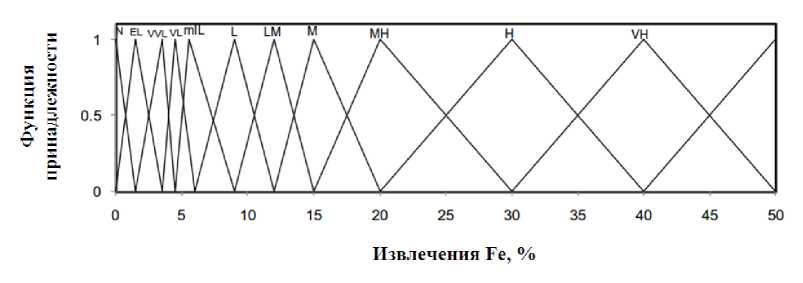
Фаззификация — это процесс нахождения степеней принадлежности. Функция принадлежности (ФП) — это кривая, которая определяет, как каждая точка во входном пространстве отображается в значение принадлежности (или степень принадлежности) между 0 и 1 (Fuzzy Logic Toolbox). Значение 0 представляет полное отсутствие принадлежности, значение 1 представляет полную функцию принадлежности, а промежуточные значения используются для представления частичной принадлежности. Входные и выходные переменные были фаззифицированы в соответствии с лингвистическими наборами, показанными в таблице 1. Экспериментальные результаты и экспертные знания были использованы для получения чисел входных функций принадлежности. Как видно из рисунков 2-4, треугольные функции принадлежности (1) использовались для получения входной переменной времени и выходных переменных восстановления золота и железа. Каждая функция принадлежности на 30–60 % перекрывается с соседними.
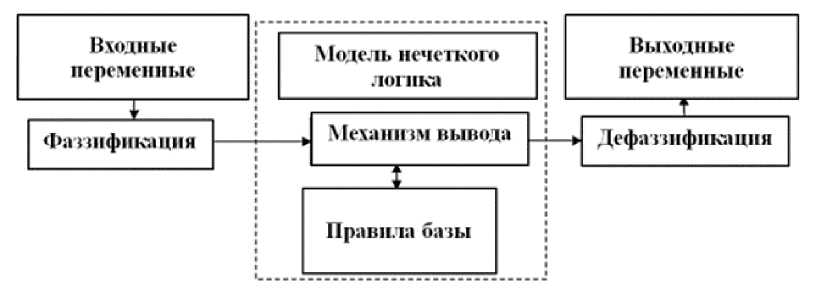
Рисунок 1. Структурная схема нечеткой логики.
Figure 1. Block diagram of fuzzy logic.
Обычные множества являются частным случаем нечетких множеств, в которых функция принадлежности принимает только два значения: 0 (непринадлежность) и 1 (принадлежность). Принимая во внимание это примечание, входные переменные и тип бактерий были определены как четкие наборы, которые затем были обработаны в соответствии с уравнениями (2) и (3). Для переменной, когда функция принадлежности находится в диапазоне от 0 до 0,5, выбирается метод бактериального окисления (БО), а когда она находится в диапазоне от 0,5 до 1, выбирается метод бактериального окисления. Для переменной, когда функция принадлежности находится в диапазоне от 0 до 0,5, выбираются ацидофильные бактерии (АБ), а когда она находится в диапазоне от
0,5 до 1, выбираются умеренно термофильные бактерии.
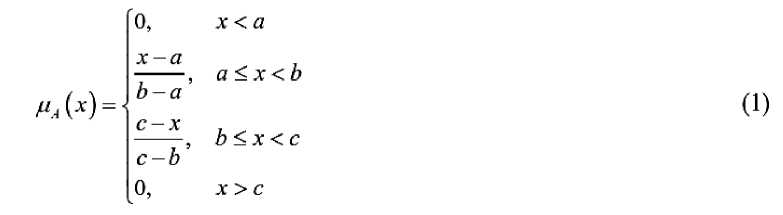
– функция принадлежности нечеткого множества; a, b, c – постоянные.
0 < x < 0.5 for BL
0.5 < x <1 forELB
/^Method (Ж)
L
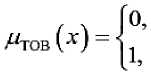
0 0.5 < x < 1 for MT функции принадлежности переменных «Метод» и «ТБ». / Нечеткие правила могут быть получены как из рассуждений эксперта и лингвистических выражений, так и из отношений между системными переменными. Для моделирования процесса была построена система на основе нечетких правил с 34 нечеткими правилами «ЕСЛИ-ТО» (таблица 2). Отношения показывают некоторые из определенных правил системы, основанной на нечетких правилах Мамдани. Правила в базе содержат нечеткое И в предшествующей части. Для моделирования логического оператора И можно использовать основной оператор, который дает минимальные степени принадлежности между двумя нечеткими множествами элементов. Таблица 1. Лингвистические выражения, используемые во входных и выходных переменных. Table 1. Linguistic expressions used in input and output variables. Символ Значение Символ Значение Символ Значение НЗ Незначительный Н Низкий БМВ Более или менее высокий ЧН Чрезвычайно низкий НС Низкий средний В Высокий ООН Очень-очень низкий БМС Более или менее средний ОВ Очень высокий ОН Очень низкий С Средний ООВ Очень-очень высокий БМН Более или менее низкий СВ Средний высокий ЧВ Чрезвычайно высокий Таблица 2. Нечеткие правила извлечения золота и железа (тип бактерий (ТБ), бактериального окисления (БО), электробиовыщелачивание (ЭБВ), ацидофильных бактерий (АБ), умеренно термофильные бактерии (УТБ)). Table 2. Fuzzy rules for the extraction of gold and iron (type of bacteria (TB), bacterial oxidation (BO), electrobiological leaching (EBV), acidophilic bacteria (AB), moderately thermophilic bacteria (UTB)). ЕСЛИ ТО И И И Комб. Метод ТБ Время Золото Железо 1 БО АБ ЧН ЧН БМН 2 БО АБ ОН ООН ООН 3 БО АБ Н ОН Н 4 БО АБ НС БМН Н 5 БО АБ М Н НС 6 БО АБ СВ НС М 7 БО АБ В НС М 8 БО АБ ОВ БМС М 9 БО АБ ЧВ М М 10 БО УТБ ЧН ООН Н 11 БО УТБ ОН ООН Н 12 БО УТБ Н ОН НС 13 БО УТБ НС НС СВ 14 БО УТБ М НС СВ 15 БО УТБ СВ БМВ СВ 16 БО УТБ В БМВ В 17 БО УТБ ОВ ОВ В 18 БО УТБ ЧВ ОВ В 19 ЭБВ АБ ЧН ОН СВ 20 ЭБВ АБ ОН БМН СВ 21 ЭБВ АБ Н Н СВ 22 ЭБВ АБ НС М СВ 23 ЭБВ АБ М СВ В 24 ЭБВ АБ В БМВ В 25 ЭБВ АБ ЧВ ОВ В 26 ЭБВ УТБ ЧН БМВ М 27 ЭБВ УТБ ОН Н СВ 28 ЭБВ УТБ Н СВ СВ 29 ЭБВ УТБ НС БМВ В 30 ЭБВ УТБ М БМВ СВ 31 ЭБВ УТБ СВ ООВ ОВ 32 ЭБВ УТБ В ООВ ОВ 33 ЭБВ УТБ ОВ ООВ ОВ 34 ЭБВ УТБ ЧВ ЧВ ЧВ Рисунок 2. Функции принадлежности нечеткой логики для переменной времени (вход). Figure 2. Fuzzy logic membership functions for a time variable (input). Рисунок 3. Функции принадлежности нечеткой логики для извлечения Au (переменная отклика). Figure 3. Fuzzy logic membership functions for extracting Au (response variable). Рисунок 4. Функции принадлежности нечеткой логики для извлечения Fe (переменная отклика). Figure 4. Fuzzy logic membership functions for extracting Fe (response variable). Интерпретируя нечеткое И, как минимум, можно переписать правила в более лаконичной форме: Rj: if x is^; then у is£;, j = 1,2,---,г (4) где x% содержит входные переменные, как и выходная переменная, и: Каждое правило соответствует нечеткому отношению, заданному уравнением (6): ^W = 4(JHW <6) Механизм нечеткого вывода является ядром нечеткой системы. Он используется для моделирования способов мышления и принятия решений людей для решения проблем [4]. После перевода каждого правила в следующим шагом будет объединение всех правил вместе. В самом деле, каждое правило создает нечеткое множество в выходном пространстве как , и, таким образом, необходимо агрегировать все выходные данные, чтобы получить одно нечеткое множество в Y. Общий результат можно рассчитать с помощью синтеза Ларсона как: Процесс сокращения конечного полученного нечеткого набора называется дефаззификацией, который преобразует выходной нечеткий набор, выведенный из механизма нечеткого вывода, в обычное значение в пространстве Y. Наиболее распространенным методом дефаззификации является центр, который дает центр тяжести соответствующего выходного нечеткого множества следующим образом: JyCr (y)dy Л-^^у id ’ y^Y (8) где y*(x) — центр тяжести площади, покрываемой функцией. Моделирование сложного и нелинейного поведения бактериального окисления золота было выполнено с помощью модели нечеткой логики. База знаний, содержащая правила «ЕСЛИ-ТО», была разработана на естественном языке для хранения опыта человека-эксперта. Изменение извлечения золота и железа рассматривалось в процессах бактериального окисления с использованием как смешанных ацидофильных бактерий, так и смешанных умеренно термофильных бактерий. Они ясно показывают, что восстановление можно очень хорошо предсказать с помощью нечеткой модели, в которой R-квадрат модели больше 0,99 во всех случаях. Рисунок 5. Сравнение данных извлечения золота, полученных в результате экспериментов. Figure 5. Comparison of gold recovery data from experiments. Из рисунка 5 видно, что модель нечеткой логики может прогнозировать извлечение при очень малых и очень больших значениях, и модель хорошо учитывает нелинейное поведение извлечения золота и железа в различных условиях. Нечеткая модель также может быть мощным инструментом для использования в системе управления биореактором с мешалкой при условии формирования полной нечеткой базы знаний на основе опыта людей-экспертов и реальных данных, полученных в ходе экспериментов. ЗАКЛЮЧЕНИЕ В работе получена модель нечеткой логики для прогнозирования извлечения золота и железа из пиритного медного концентрата традиционными и электрохимическими методами бактериального окисления. Извлечение этих металлов является целевым направлением гидрометаллургического извлечения золота из медных флотоконцентратов. Входными переменными были метод процесса бактериального окисления, тип бактерий и время. Между указанными входными данными и выходными данными была разработана нечеткая связь с помощью правил «если-то». Сравнение экспериментальных данных и расчетных значений модели показало их хорошее совпадение, при котором R-квадрат модели составлял более 0,97 в каждой серии данных. Результаты показали способность нечеткой модели гибко прогнозировать сложные и нелинейные процессы бактериального окисления, и она является мощным инструментом для извлечения металлов в такой сложной системе.