Моделирование некомпланарного межпланетного перелета космического аппарата с солнечным парусом с учетом особенностей движения относительно центра масс

Согласно Федеральной космической программе России на 2016–2025 годы, утвержденной постановлением Правительства РФ от 23 марта 2016 года № 230, одной из основных задач является выполнение международных обязательств «по участию не менее чем в двух миссиях в рамках международной кооперации по исследованию Марса, Венеры, Меркурия и Солнца, в осуществлении полетов автоматических космических ап-

паратов (КА) к планетам и телам земной группы». Исследование планет и околосолнечного пространства предоставляет возможность найти ответы на многие фундаментальные вопросы формирования Солнечной системы, возникновения и развития жизни на Земле. Перспективным путем снижения стоимости подобных миссий является использование физических принципов, не связанных с затратами рабочего тела, для формирования заданных гелиоцентрических траекторий, например, движение с помощью солнечного паруса (СП). СП – это приспособление, использующее давление солнечного света на отражающую поверхность для приведения в движение КА [1]. Значительное

К1ЛЕ АППАРАТЫ Ш

Том 4

преимущество использования СП состоит в том, что он способен заменить двигательную установку на борту малого КА. Отсутствие рабочего тела позволяет существенно уменьшить массу всего КА и продлить срок его активного существования.

Недостаточно изучен вопрос движения относительно центра масс (ЦМ) КА с СП каркасного типа, который необходимо учитывать при формировании программ номинального управления КА. В работах [2-5] описаны способы управления ориентацией СП роторного типа с помощью тонкопленочных элементов управления (ТЭУ), 142 не требующих применения механических воздействий. ТЭУ располагаются в дискретных областях на поверхности СП и способны изменять отражательную способность. При изменении напряжения, подающегося на ТЭУ, он становится прозрач- ным или непрозрачным, возникает разница нормальных составляющих сил светового давления, обеспечивающая создание управляющего момента для изменения ориентации КА в пространстве.

Работы, посвященные анализу этой перспективной возможности управления ориентацией КА с СП каркасного типа в пространстве с помощью ТЭУ при совершении некомпланарных межпланетных перелетов, отсутствуют. Следовательно, обоснование успешного применения программы управления гелиоцентрическим перелетом с заданными проектными параметрами КА с СП является актуальной научной проблемой.

1.    Постановка задачи

Рассматривается межпланетный некомпланарный перелет КА с неидеально отражающим СП с гелиоцентрической орбиты Земли к Венере. Неидеально отражающий СП – это СП, величина и направление ускорения от которого рассчитываются с учетом зеркального и диффузного отражений, поглощения и пропускания фотонов поверхностью СП. Предполагается, что КА выведен из сферы действия Земли с помощью разгонного блока. Цель перелета – попадание в сферу Хилла планеты – области пространства, в которой могут двигаться тела, оставаясь спутником планеты. Для выполнения поставленной цели достаточно чтобы расстояние между КА и планетой Dist было меньше радиуса Хилла планеты R _Хилла при значении интеграла энергии КА h меньше нуля.

Введем систему координат OPNS, связанную с СП (рис. 1). Точка O является центром системы координат и совпадает с ЦМ КА с СП. Ось OP направлена по вектору р, лежащему в плоскости СП и совпадающему с проекцией на поверхность СП радиус-вектора r. Ось ON направлена по вектору нормали СП n в сторону от источника света. Ось OS лежит в плоскости СП и дополняет систему координат до правой. Угол X между век- тором нормали n и радиус-вектором r будем называть углом установки СП или управляющим углом.

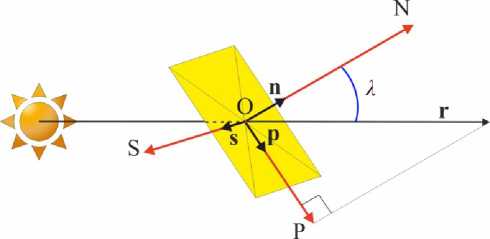
Рис. 1. Система координат OPNS, связанная с СП

Введем вектор фазовых координат X , описывающий движение ЦМ и движение относительно ЦМ КА в комбинированной системе координат [6]:

X = (r, u, Vr, Vu, Q, i, 0 p, 0 n, 0,, ю p, ю n, ю, )Т, где r – гелиоцентрическое расстояние КА с СП; и - аргумент широты; Vr, Vu - радиальная и трансверсальная скорости; Ω – долгота восходящего узла орбиты; i - наклонение орбиты; 9p, 9n, 9s - углы поворота СП относительно осей OP, ON, OS; ωp, ωn, ωs – соответствующие угловые скорости.

Поскольку в работе рассматривается КА каркасного типа, то нет необходимости управлять собственным вращением СП относительно оси ON. Для описания номинального управления движением КА вводится вектор U [6]:

U = {8 p (t), 8, (t)}", где 8p(t), 5s(t) - функции номинального управления, определяющие вращение СП относительно осей OP и OS соответственно. Функции δp(t) и δs(t) принимают значение «+1» при увеличении угла установки СП X, «-1» - при уменьшении угла установки СП X, «0» - при неизменности ориентации СП. Собственное вращение СП относительно оси ON не учитывается. В работе рассматривается последовательное управление, что исключает возможность вращения относительно двух осей одновременно. Данное допущение должно быть обусловлено неравенством:

18 p ( t )| + |8 , ( t ) < 1.

Фиксированный вектор проектных параметров prm КА с СП описывается следующим образом [6]:

prm = {m, m m, 5, р, р r ,р d, а, т, h тэу }г, где m - масса КА с СП; mСП - масса СП; S - площадь СП; р - коэффициент отражения поверхности СП; ρr – коэффициент зеркального отражения поверхности СП; ρd – коэффициент диффузного отражения поверхности СП; а - коэффициент по- глощения фотонов поверхностью СП; τ – коэффициент пропускания; hТЭУ – ширина ТЭУ.

Параметры вектора фазовых координат X и вектора управления U должны удовлетворять следующим ограничениям:

ωдост ≤ ω < ωпред , где ωдост – достаточная угловая скорость, необходимая для выполнения программного разворота; ω – вектор угловой скорости КА; ωпред – предельная угловая скорость, при которой КА будет испытывать критические нагрузки.

Граничные условия гелиоцентрического перелета обеспечивают попадание КА с СП в сферу Хилла планеты и записываются следующим образом [6]:

X ( t 0 ) = X o , X ( t k ) = X k .

В качестве основного критерия оптимальности выбрано минимальное время перелета t_k → min:

U opt ( t ) =

= arg min t k ( U |prm e P , X⁽ t о ) = X_o , X⁽ t k ) = X k ) .

u ( t )

Предлагается следующая процедура решения данной задачи:

• •    получение номинальной программы управления движением ЦМ КА;

• •    определение достаточных угловых скоростей для обеспечения полученной программы номинального управления, расчет параметров органов управления ТЭУ;

• •    моделирование совместного движения ЦМ и относительно ЦМ для демонстрации реализуемости полученной программы управления.

• 2.    Математическая модель движения

В рамках данной работы рассматривается модель плоского неидеально отражающего СП со следующими допущениями [6]:

• •    ρ = const ≠ 0, α = const ≠ 0, τ = const ≠ 0;

• •    рассеивание диффузно отраженных фотонов происходит равномерно во всех направлени-

• ях в полуплоскости, соответственно, направление результирующего вектора силы от рассеянных фотонов совпадает с направлением нормали к СП;

• •    излучение на поверхности СП от нагрева поглощенных фотонов происходит равномерно по всем направлениям в полуплоскости, т. е. результирующий вектор силы тяги от поглощенных фотонов совпадает с направлением падения фотонов.

Принятые допущения позволяют сформировать новую модель неидеально отражающего СП. Введем подвижную объектоцентрическую систему координат ORUZ (рис. 2), которая используется при моделировании гелиоцентриче-    ¹⁴³

ского движения КА с СП. Точка O – центр системы координат, совпадающая с ЦМ КА. Ось OR направлена по радиус-вектору r в сторону от источника света. Ось OU лежит в плоскости орбиты и направлена по движению КА. Ось OZ перпендикулярна плоскости орбиты и дополняет систему координат до правой. Положение плоскости орбиты определяется долготой восходящего узла Ω и наклонением i .

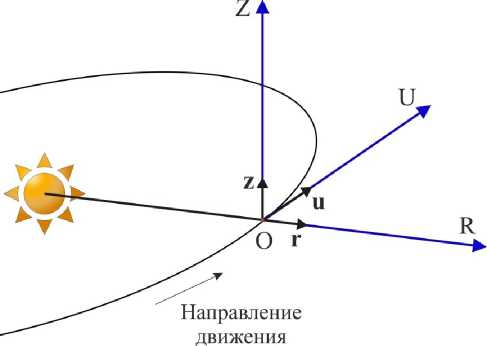
Рис. 2. Подвижная объектоцентрическая система координат ORUZ

Вектор полного ускорения a в системе координат ORUZ с учетом особенностей отражательной способности поверхности СП записывается следующим образом:

a

p

sin Xj

cos ² X₂ +

a

r

к

Г

sin X₂ I       .  .        .

-----¹ I + sin X₂ cosXj к sin X_, J

sin ² X —

² 1 sin X₂ I к      J

+ a „ cos X₂ cos Xj

a = a u

az

a p

sin X 1 sin X 2

sin X2 —

к

² sinkl I _к sin X[ J

—

cos ² X 2 +

sin X2 I       .

-----¹ I cosX , _к sin Xj J

+ a n cosX 2 sin X 1

;

sin X₂ I          .  .

a_p cosX₂

sin ² X —

. _л² I — a n sin X 2 к sin X_, J

(оСМИЧЕскиЕ

АППАРАТЫ И

Том 4

a p = P 3

R о Y

f

r J m

— cos X 1 cos X ₂ 1 — p + a

⁸ f B f

—

8 ₆B?

к

⁸ f ⁺⁸ b

■ sin ² X 1 cos ² X ₂ + sin ² X ₂;

J

а -Р I R0 I an = РЗI      I

S

r ) m

S

— cos X 1 cos X 2 1 + p + a

⁸ J Bf

—

8 b B b )

.

к

⁸ f ^{+ 8} b )

Здесь PЗ - давление отвесно падающего солнечного света на полностью поглощающую поверхность «абсолютно черного» тела на орбите Земли, PЗ = 4,55И0"6 Н^м-2; R0 - среднее расстояние между 144   ЦМ Солнца и Земли, R0= 1 а.е.; еf, еb - коэффициен ты излучения освещенной и теневой стороны СП; Bf, Bb – коэффициенты эмиссионной диффузии освещенной и теневой стороны СП соответственно; Х1 - угол между радиус-вектором и проекцией нормали СП на плоскость орбиты; λ2 – угол между нормалью СП и ее проекцией на плоскость орбиты.

В табл. 1 приведены оптические характеристики поверхности неидеально отражающей модели СП.

Таблица 1

Оптические характеристики поверхности СП

Модель	Оптические коэффициенты поверхности СП
	ρ	ρ r	ρ d	α	ε f	ε b	B f	B b	τ
Неидеально отражающий СП [7]	0,87	0,94	0,06	0,12	0,05	0,55	0,79	0,55	0,01

Сформирована математическая модель гелиоцентрического движения ЦМ КА, которая описывается традиционной системой дифференциальных уравнений в комбинированной системе координат с учетом гравитации Земли и Венеры [8].

Движение относительно ЦМ КА осуществляется за счет изменения отражательных свойств ТЭУ (рис. 3). Пусть фотоны падают на поверхность СП по направлению нормали n к СП. С одной стороны СП ТЭУ отключены от подачи тока, поэтому на эту сторону СП от падающих и отраженных фотонов будет действовать сила F 1 . На ТЭУ с другой стороны СП подано напряжение, в результате чего на эту сторону СП от падающих и поглощенных фотонов будет действовать сила F ₂.

Очевидно, что F 1 > F ₂. За счет разницы нормальных составляющих сил светового давления A F = F 1 - F ₂, действующих на ТЭУ, создается внешний момент, влияющий на ориентацию СП. Подобное управление было успешно испытано на КА с СП IKAROS [9]. ТЭУ, меняющие свои отражательные свойства, позволяют управлять пространственной ориентацией СП без использования гироскопов, корректирующих двигателей и других устройств, что, в результате, уменьшает массу всей конструкции КА с СП.

Математическая модель движения относительно ЦМ с учетом особенностей отражательной способности поверхности СП и ТЭУ, а также размеров ТЭУ описывается следующим образом:

О p = ю p

⁰ n = ^ю n

*

О 5

= ^d 5

12 Р з

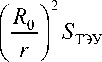
cosX 1 cos X₂ х

к

^Ю Р

Х

к

cosX 1 cosX₂ р _r р + а к

⁸ f B f

- ⁸ b B b ^

⁸ f ⁺⁸ b J

^{+ (}1 ^-р r ) р B f   ⁽ ^S ⁺ h ТЭУ ) ^{+ d} n ^ю 5

_ m СП ^S

d) n = 0

ю

Х

к

(

12 P З

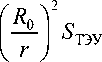
cosX 1 cosX₂ х

( cosX1 cosX2 рrр + а к

⁸ f B f

^-8 b B b )

⁸ f ⁺⁸ b J

^{+ (}1 ^-р r ) р B f ^И+^ ТЭУ^ + ^d p to n

_    m СП ^S

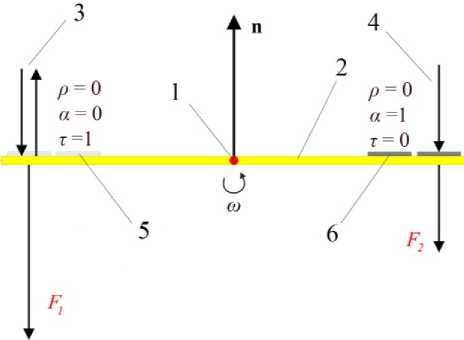
Рис. 3. Принцип работы ТЭУ ориентацией СП (1 – ЦМ КА; 2 – СП; 3 – падающие и отраженные фотоны; 4 – падающие фотоны; 5 – ТЭУ, питание выключено; 6 – ТЭУ, питание включено)

ЦМ КА рассматривается как точка сосредоточенной массы, разворот осуществляет только СП, обладающий массой mСП. Разработанная математическая модель движения КА с неидеально отражающим СП позволяет анализировать воз можность управления крупногабаритной тонкопленочной конструкцией для реализации перелетов между некомпланарными гелиоцентрическими орбитами.

• 3.    Результаты моделирования некомпланарного перелета Земля–Венера с учетом движения относительно центра масс

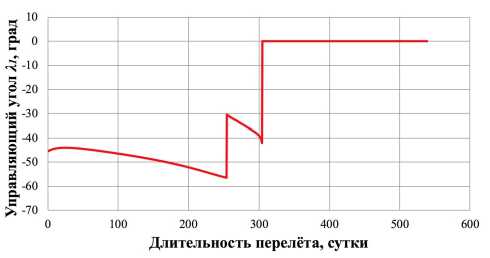
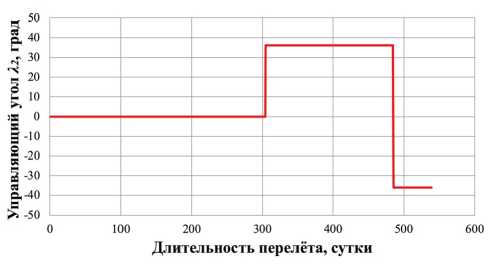
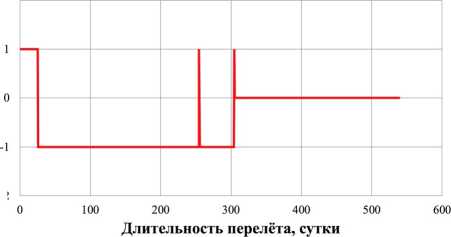
В соответствии с процедурой решения поставленной задачи было проведено моделирование движения ЦМ КА массой 39,8 кг с неидеально отражающим СП площадью 500 м 2 и получено номинальное управление движения для осуществления перелета Земля-Венера (рис. 4 и 5). Управляющие углы X j и X 2 и функции управления 5 p и 5 ^ описывают номинальную программу управления движением КА с СП. Процедура формирования номинальных программ управления движения КА с СП, основанная на базе использования законов локально-оптимального управления (ЗЛОУ), рассмотрена в [10].

аб

Рис. 4. Зависимости управляющих углов во времени: а ) угол X j ; б) угол X 2

а

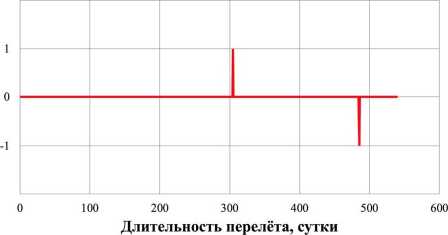
б

Рис. 5. Зависимости функции управления во времени: а ) функция управления δ _p ; б ) функция управления δ _s

По результатам проведения моделирования движения ЦМ КА с неидеально отражающим СП выявлено, что для реализации гелиоцентрического некомпланарного перелета ЦМ КА с неидеаль- но отражающим СП с орбиты Земли к Венере на расстояние 579 226 км потребовалось 539 суток. Интеграл энергии достиг значения -0,140 км2·с-2, что ниже нуля. Полученные значения расстояния

KI/IEАППАРАТЫ 1/1

Том 4

до Венеры и интеграла энергии демонстрируют возможность КА двигаться внутри сферы Хилла, оставаясь спутником планеты. Из этого следует, что полученная программа номинального управления позволяет выполнить поставленную задачу.

Далее, в соответствии с процедурой решения поставленной задачи, определены максимальная достаточная угловая скорость ω_дост и ширина ТЭУ h ТЭУ для реализации найденной программы номинального управления. Графики изменения угловых скоростей ω _p и ω _s относительно осей OP и OS приведены на рис. 6.

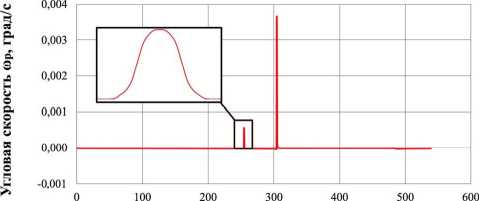
Длительность перелёта, сутки

а

На рис. 7 представлен модуль вектора угловой скорости |ю|, с помощью которого и определены достаточные угловые скорости и необходимые габариты ТЭУ По рис. 7 видно, что весь перелет можно условно разделить на 7 участков – 3 с резким изменением угла управления (участки 2, 4, 6) и 4 с плавным изменением ориентации СП (участки 1, 3, 5, 7). Для каждого участка определена максимальная достаточная угловая скорость и габариты ТЭУ в зависимости от расстояния от источника света и управляющего угла. Результаты расчета представлены в табл. 2.

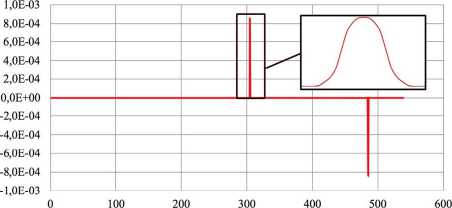
Длительность перелёта, сутки

б

Рис. 6. Зависимости угловой скорости во времени:

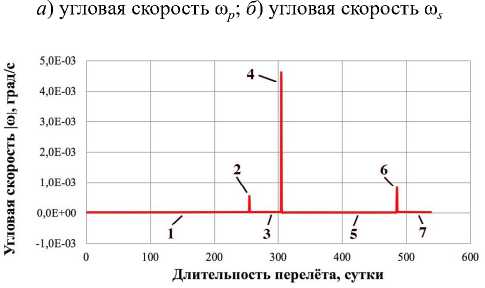
Рис. 7. Зависимости модуля вектора угловой скорости во времени

Таблица 2

К определению максимальной достаточной угловой скорости и габаритов ТЭУ

№ участка	Временной период, сут.		Расстояние до источника света, a.e.	|λ|max, град	|ω дост |, град/с	h ТЭУ , м	S ТЭУ , м2	% от S , %
	Начало	Завершение
1	0	254	1,02	-56,44	2,53∙10-5	0,235	20,780	4,156
2	254	255	0,75	-30,48	5,59∙10-4	0,123	10,940	2,188
3	255	304	0,75	-41,97	3,84∙10-5	0,011	1,000	0,200
4	304	305	0,72	36,10	4,61∙10 -3	1,062	90,487	18,097
5	305	485	0,77	36,10	2,72∙10-5	0,007	0,650	0,130
6	485	486	0,75	-36,10	8,37∙10-4	0,201	17,838	3,568
7	486	1000	0,75	-36,10	3,67∙10-5	0,009	0,800	0,160

Из табл. 2 видно, что для реализации программы номинального управления движением КА необходимо установить на СП ТЭУ шириной 1,062 м. Площадь ТЭУ SТЭУ равна 90,487 м2, что составляет около 18 % от общей площади СП. Именно такие габариты ТЭУ обеспечивают достаточную угловую скорость ωдост, равную 4,61∙10-3 град/с, на 304 день перелета на расстоянии 0,72 а.е. от источника света.

Далее проведено совместное моделирование движения ЦМ и относительно ЦМ с исполь- зованием программы номинального управления с учетом ТЭУ Получена траектория некомпланарного перелета Земля-Венера КА с неидеально отражающим СП с учетом движения относительно ЦМ КА (рис. 8).

По результатам совместного моделирования выявлено, что расстояние между КА и Венерой

Dist * достигло 205 943 км, а интеграл энергии h * равен -2,885 км²/с², что удовлетворяет условиям моделирования. В табл. 3 приведено сравнение алгоритмов использования ЗЛОУ без учета и с учетом ТЭУ, а в табл. 4 – сравнение перелетов КА с СП с орбиты Земли к Венере без учета и с учетом ТЭУ.

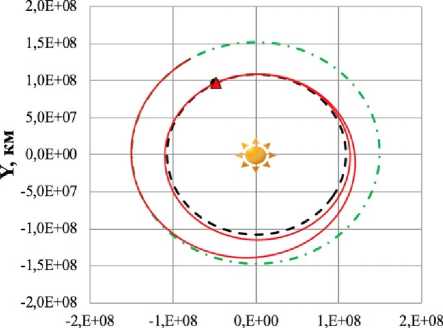
X, км

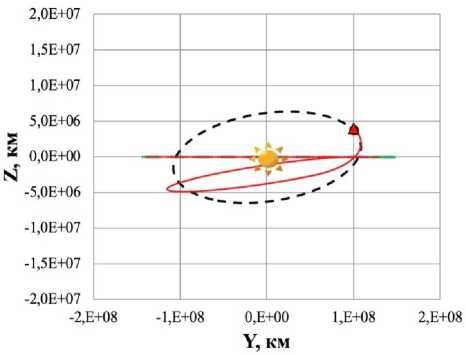
б

Рис. 8. Траектория перелета КА с СП:

а ) плоскость XOY; б) плоскость YOZ (▲ — КА; • — Венера; ♦ — Солнце; – · – орбита Земли; – – орбита Венеры; –– траектория КА)

Таблица 3

Сравнение алгоритмов использования ЗЛОУ без учета и с учетом ТЭУ

№ п/п	ЗЛОУ	Длительность, сут.
		без учета ТЭУ	с учетом ТЭУ
1	наискорейшее уменьшение радиуса перигелия, ↓ rπ	254	254
2	наискорейшее уменьшение радиуса афелия, ↓ rα	50	49
3	наискорейшее увеличение долготы восходящего узла, ↑ Ω	181	185
4	наискорейшее увеличение наклонения, ↑ i	55	58

Таблица 4

Сравнение перелетов КА с СП с орбиты Земли к Венере без учета и с учетом ТЭУ

№ п/п	Наименование	Размерность	Значение
			без учета ТЭУ	с учетом ТЭУ
1	Ширина ТЭУ, h ТЭУ	м	0	1,062
2	Площадь ТЭУ, S ТЭУ	м2	0	90,487
3	Дата старта, D 0	дд.мм.гггг	29.07.2026	28.07.2026
4	Дата завершения перелета, Dк	дд.мм.гггг	19.01.2028	25.01.2028
5	Длительность перелета	сут.	540	546
6	Расстояние до цели, Dist	км	579 590	205 943
7	Интеграл энергии, h	км2/с2	-1,035	-2,885

По результатам совместного моделирования движения ЦМ и относительно ЦМ КА с учетом ТЭУ выявлено, что гелиоцентрический некомпланарный перелет Земля-Венера реализуем для КА с СП с заданными проектными харак- теристиками. Найденная программа управления движением КА с неидеально отражающим СП обеспечивает выполнение всех необходимых и достаточных условий перелета, описанных в постановке задачи.

(оСМИЧЕскиЕ

АППАРАТЫ И

Заключение

Рассмотрен некомпланарный межпланетный перелет Земля-Венера КА массой 39,8 кг с неидеально отражающим СП площадью 500 м2 с учетом особенностей движения относительно ЦМ. Для проведения моделирования данного перелета сформирована математическая модель движения, состоящая из двух систем дифференциальных уравнений, описывающих движение ЦМ и относительно ЦМ. Проведено моделирование движения ЦМ КА, в результате которого 148   была получена программа номинального управле ния движением, позволяющая совершить перелет КА с СП с орбиты Земли к Венере на расстояние

Том 4

579 226 км за 539 суток. Поскольку основной задачей было провести моделирование движения с учетом особенностей движения относительно ЦМ, было установлено, что для совершения перелета Земля-Венера на СП необходимо установить ТЭУ площадью 90,487 м2, что составило около 18 % от общей площади СП. По результатам совместного моделирования движения ЦМ и относительно ЦМ выявлено, что длительность перелета увеличилась и составила 546 суток, а расстояние между КА и Венерой, наоборот, сократилось и достигло 205 943 км. Таким образом, гелиоцентрический некомпланарный перелет Земля-Венера реализуем для КА с СП с заданными проектными характеристиками.