Моделирование некоторых процессов тестоприготовления на основе интеграции пакетов программ Adobe ActionScript и MathCAD

При приготовлении теста для смешивания с мукой часто предварительно готовят жидкие эмульсии типа меланжа, улучшителей и структурообразователей на основе лецитина и других неньютоновских жидкостей. Эти процессы иногда включают операции фильтрования, аналитическое описание массообменных эффектов при которых вызывают весьма большие сложности. Одним из выходов из сложившейся ситуации является моделирование и воспроизведение таких операций на виртуальном оборудовании.

Язык программирования Flash ActionScript обладает широким спектром возможностей: позволяет создавать управляемую трехмерную анимацию, интерактивные действия, интегрироваться с Javascript, PHP и управлять базами данных, работать с видео и аудио информацией. Этот язык поддерживается программой Adobe Flash Player, поэтому он сегодня функционирует практически на каждом ПК, подключенном к Интернету. Программы на Flash Actionscript широко используются в вузовских системах дистанционного обучения. По данным авторов, среди различных систем дистанционного обучения отсутствуют программные системы, интегрирующие язык Actionscript с какими-либо библиотеками численных алгоритмов расчетов или математическими пакетами. В данной работе предлагается новая концепция создания дистанционных образовательных материалов в вузе (лекций, лабораторных работ) на базе интеграции языка програмирования анимации Adobe Flash Action Script c вычислительным пакетом Mathcad.

Интеграция Actionscript программы и пакета Mathcad осуществляется посредством технологии OLE Automation, которую поддерживает Mathcad, и промежуточной программы на языке Microsoft Jscript, с которой программа на языке Flash Actionscript 2.0 взаимодействует через класс ExternalInterface [1,2]. Программа Jscript поддерживает как технологию OLE Automation, так и взаимодействие с

Actionscript программой. Приведем ряд особенностей. swf-файл, содержащий Actionscript программу, должен быть встроен в html-страницу, содержащую код Jscript. Открываться html-страница должна в браузере Internet Explorer. Система безопасности браузера должна позволить использование элементов управления ActiveX, не помеченных как безопасные для использования.

Таким образом, предлагается новая создания дистанционных образовательных материалов в вузе (лекций, лабораторных работ) на базе интеграции языка програмирования анимации Adobe Flash Action Script c вычислительным пакетом Mathcad. Такая концепция обладает следующими преимуществами: 1) быстрое создание дистанционных материалов, обладающих широкими возможностями численного моделирования, анимации, интерактивных действий, встраивания видео и аудиоинформации, взаимодействия с базами данных; 2) не нужен интернет-сервер для проведения фильтровальной перегородки, ц - динамическая вязкость суспензии; p – разность давлений по обеим сторонам фильтровальной перегородки; г0=цг00, roo - удельное объемное сопротивление осадка; x0 – отношение объема осадка к объему фильтрата в начальный момент фильтрования.

Значения времени т ₀ и удельного объема фильтрата q 0 при которых заканчивается первая стадия процесса фильтрования определялись решением системы уравнений

' x nach ^- W ^{T -} q = x о ( q ^{+ W T)} , s

т = f (q)• где xnach – высота уровня суспензии в фильтре в начальный момент фильтрования, отсчитываемая от фильтровальной перегородки; f(q) – функция из формулы (1).

Скорость стесненного осаждения W(d,c) в формулах (1) и (2) как функция диаметра частиц мела d и объемной доли мела с рассчиты- численных расчетов, время расчета мало, т.к.

для расчетов используется компьютер посетителя вэб-сайта.

В качестве примера реализации предлагаемой новой концепции дистанционных обучающих материалов была создана виртуальная лабораторная работа «Фильтрование суспензий при наличии осаждения». В файле пакета Mathcad рассчитывалась математическая модель фильтрования суспензии при наличии осаждения с образованием несжимаемого осадка. Модель состояла из двух стадий.

Во время первой стадии фильтрования одновременно происходит расслаивание суспензии за счет осаждения и фильтрование суспензии. Для описания первой стадии процесса была использована следующая зависимость между удельным объемом фильтрата q

валась в предположении ламинарного режима по формуле:

d2g(Рт-Рж)(1-с)Ф(с).

18ц( с)          ;

W (d, c)

Ф (с) = 10-L82 с,

где р _т , _ж - плотность мела и воды соответственно. В формуле (3) динамическая вязкость суспензии ц (с) рассчитывалась по формуле для суспензии сферических частиц, верной при с < 0.3 [5]:

Ц( c )=              Цжс                  (4)

1-                                  0.469

0.46-0.0015 |цжр/ I

v / р ж J

Вторая стадия процесса фильтрования при наличии осаждения описывается фильтро-

и временем т , подтвержденная для несжимаемого осадка [3]:

ванием воды через слой осадка постоянной вы-

соты h 0 по формуле

R nWq

т=f (q) = -+— —

V W Р д n = rrX^, p

-1)

q (т) =

nW J

p (т-т0) Rf + r0 h0

^{+ q} 0 ; ,

где: W – скорость стесненного осаждения частиц мела; R f = ^ R ф_п , R ф_п - сопротивление

h0 = x0 (q0 + Wт0), (5)

где R f , r 0 , x 0 , W, p определены как в формуле (1); т ₀ и q₀ - решение системы (2). Далее полученная по формулам (1) и (5) зависимость q( T ) в

Моделирование некоторых процессов тестоприготовления на основе интеграции пакетов программ Adobe ActionScript и MathCad обеих стадиях процесса фильтрования аппрок-

Actionscript программу для создания анимации симировалась функцией

q (т) = a^ + ax T + a—T + a3

Значения r0, x0, W, Rf были взяты из экспериментов по фильтрованию водных суспензий мела при различных концентрациях мела, при наличии и отсутствии осаждения, варьировались также число и тип фильтровальных бу маг..

наполнения сборника фильтратом.

При использовании данной работы в учебных целях в дистанционном режиме (через Интернет, см. рис. 1) студент может выполнять виртуальное математическое моделирование с помощью пакета Mathcad, варьируя следующие параметры: давление, концентрацию и диаметр частиц мела, тип и число фильтровальных перегородок, наличие или отсутствие осаждения.

Параметры a 0 , a 1 , a 2 , a 3 в (6) после расчета в пакете Mathcad передавались в Flash

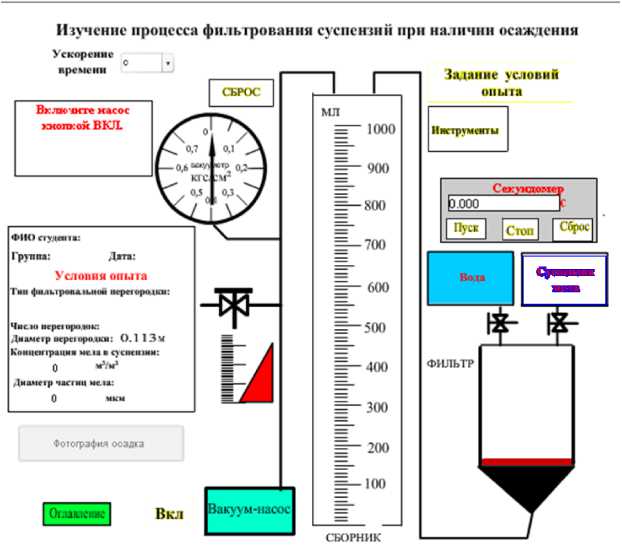
Рисунок 1 . Общий вид виртуальной установки для фильтрации