Моделирование нестационарного контакта в подшипнике качения

Введение. Расчет упруго-гидродинамического контакта ролика с деформируемой поверхностью является довольно сложной задачей, так как требует совместного решения уравнений гидродинамики в смазочном слое и уравнений упругости в деформируемом теле [1–10]. Эта задача связана с проблемой моделирования подшипников качения, которые широко используются в авиационных и ракетных двигателях. При работе подшипниковых узлов часто возникают вибрации, связанные с резкими изменениями нагрузки. Это особенно заметно в моменты запуска и остановки механизма, а также при воздействии переменной внешней силы. Эти вибрации существенно влияют на работу подшипника, увеличивая его износ и сокращая срок службы. Поэтому моделирование нестационарного режима работы подшипникового узла является важной задачей. Целью данной работы является анализ нестационарных режимов работы роликового подшипника качения в случае переменной внешней нагрузки.

Описание метода расчета. Рассмотрим контактное взаимодействие цилиндрического ролика с движущейся пластиной, покрытой слоем смазочного материала (рис. 1). Так как радиус ролика очень мал по сравнению с радиусом кольца, по которому он катится, то можно приближенно принять внешнее кольцо подшипника плоской пластиной [7].

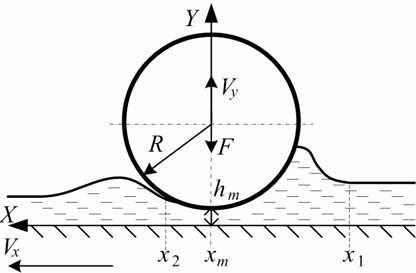
Рис. 1. Схема расположения ролика, пластины и слоя жидкого смазочного материала

Распределение давления в смазочном слое определяется из решения уравнения Рейнольдса:

af,з           ap)        fah 2 ah h exp(-a P)    = 6цпV    + axl              axJ     0 lax vat где P – давление в смазочном слое; V – скорость движения пластины; ц0 - динамическая вязкость масла при нормальном давлении; ah / at - вертикальная скорость ролика; а - пьезокоэффициент давления [11–13]. Ось x ориентирована в направлении движения пластины. Данное решение было подробно рассмотрено ранее в [14], поэтому для сравнения рассмотрим случай контакта бесконечно жесткого ролика с упругой пластиной без учета изменения вязкости в смазочном слое. В этом случае уравнение Рейнольдса имеет вид

= 6 ц V

a h 2 ah)

---1---I . ax v at)

В предположении, что площадка контакта цилиндра и плоскости мала по сравнению с радиусом кривизны R , имеем следующее выражение для толщины слоя смазочного материала [2]:

h = h m + ( x - x m ) ² / ( 2 R ) ,              (3)

где h m – минимальная толщина смазочного слоя; x m – координата точки минимального зазора.

Граничные условия в рассматриваемом случае имеют следующий вид [1; 2]:

^P ( ^x 1 ) = ^P ( x 2 ) = Ц ( x 2 ) = 0,

где x 1 и x 2 – входная и выходная границы смазочного слоя.

Для удобства решения задачи вводим безразмерные переменные:

^x = ( x ^- x m )/\^h m^R ,

q = Ph m .⁵ / ( 6 ц V^ ) ,

t = tV / 4Rh m ,

V _y hR

£ =            ,

V h

m

преобразуем исходное уравнение Рейнольдса (2) к более простому виду:

H5 1 + 2 s , a x

где H ( x ) = 1 + 5c ² /2.

Положения входной и выходной границ будем характеризовать безразмерными параметрами a и c . Значение параметра a зависит от количества смазки. В случае обильной смазки полагаем a = -« [2-4].

Интегрируя уравнение (6) и используя нулевое граничное условие (5) для производной функции давления при x = c, получаем дифференциальное урав- нение первого порядка:

a q = H ( 5с ) - H ( c ) 2 e ( xc - c ) ^a xx H ( xc ) 3 H ( x ) 3 = ⁽ 5c - c ) /2 2 s ( 5c - c )

( 1 + x 2 /2 ) 3 ( 1 + x 2 /2 ) 3

Решение уравнения (7) зависит от безразмерного параметра s , который связан с нормальной скоростью перемещения ролика. Интегрируя уравнение (7) для различных значений ε, находим распределение давления в смазочном слое, соответствующее различным нормальным скоростям ролика.

По найденному распределению давления определяем безразмерную несущую способность, являющуюся функцией параметра ε:

W '( s ) = j q ( x , s ) dx . (8)

a

Расчеты показывают, что зависимость несущей способности от ε очень близка к линейной (рис. 2), и ее можно записать в следующем виде:

W ' = W _o + A s ,                  (9)

где постоянные коэффициенты W ₀ ^' и A равны 0,401 и 1,125 соответственно.

График зависимости несущей способности W' от нормальной скорости ε в безразмерных единицах представлен на рис. 2.

С учетом соотношений (5) преобразуем выражение (8) к размерному виду:

Принимая h 0 в качестве базового зазора, вводим безразмерные переменные:

h m = h ' h 0 , t = t ' т ,

A Rh ₀

T= ,

VW 0^'

W = w '6 ^ VR _е + a 6 ^ 2 v .

3/2 y m       hm

Здесь первое слагаемое выражает зависимость стационарной несущей способности от зазора при нулевой нормальной скорости

Используя нормировки (15), приводим уравнение динамики к безразмерному виду:

d ² h '1 dh '1

m --T +--w—- 77 = -1, dt'2 h '3/2dt'h'

mV ² ( W 0^' ) ²

m =----=------ .

A ² FR

W 0

=. V 0 h_m

а второе слагаемое учитывает влияние нормальной скорости. Коэффициент перед скоростью будем называть коэффициентом демпфирования X :

X = A

6 ц R ^3/2

h

3/2 m

Движение ролика по нормали определяется уравнением динамики md^hm + X(hm) dh' - Wo(hm) = - F,(13)

dt2

где m – масса ролика; F – внешняя нагрузка.

С учетом зависимостей (11), (12) уравнение (13) принимает следующий вид:

+ A 6   ^ - W= - F.(14)

dt 2 h_m 3/2 dt 0 h_m

Полагая равными нулю производные по времени, определяем равновесное значение зазора:

6 ц VRW 0 F

Уравнение (16) определяет зависимость зазора от времени в процессе установления стационарного режима. Характерное время переходного процесса характеризуется параметром т .

Анализ влияния деформаций и зависимости вязкости от давления. Далее переходим к более реалистичной задаче с учетом прогиба поверхности и переменности вязкости, зависящей от давления в смазочном слое. Для расчетов используем следующие числовые параметры: h_m = 0,00000035 м, ц = 0,024 Па^с, α = 0,75∙10^–8 1/Па – пьезокоэффициент вязкости, V = 7 м/с, R = 0,005 м (за основу взят подшипник 32114 серии [15]). Для моделирования примем, что материал пластины имеет следующие механические свойства: E = 2,1∙10¹¹ Па – модуль упругости (сталь), m = 0,3 – коэффициент Пуассона.

Решая уравнение (7) при ε = 0, получаем распределение давления в смазочном слое (рис. 3), которое далее используем для определения прогиба упругой поверхности.

При проведении итерационного расчета прогиба поверхности применяем найденную ранее функцию податливости пластины [14]. График этой функции показан на рис. 4. Значения функции нормированы к её максимальному значению: K max = 3,267·10^–15 Па^–1.

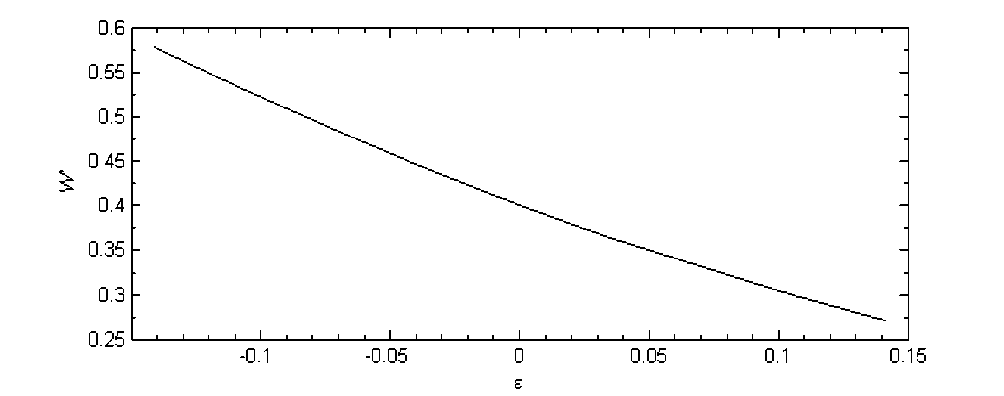
Рис. 2. Зависимость несущей способности от вертикальной скорости в безразмерных единицах

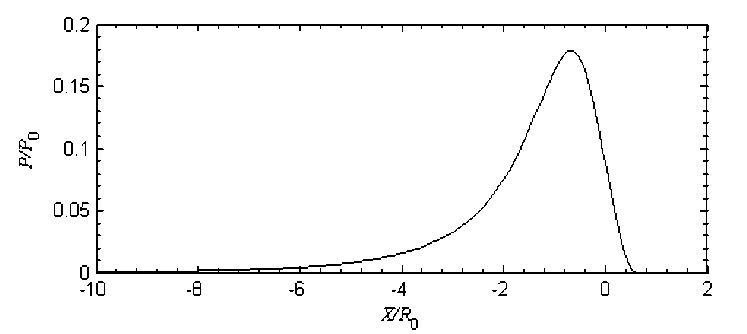
Рис. 3. Распределение давления в смазочном слое

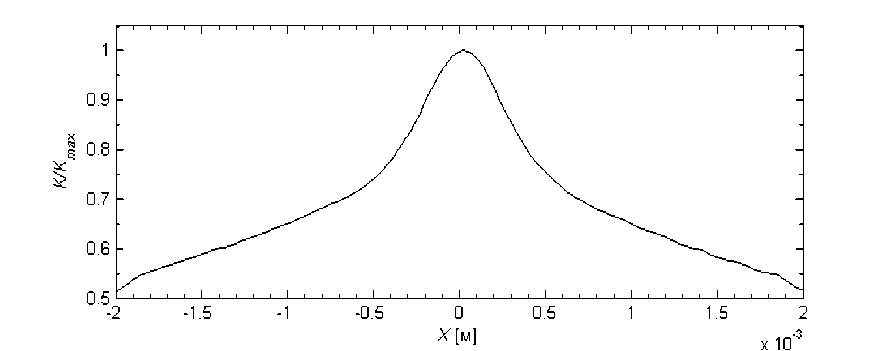
Рис. 4. График функции податливости

Исследуем влияние прогиба поверхности и пьезокоэффициента вязкости на максимум давления в смазочном слое. Данные расчетов, в которых пьезокоэффициент был фиксирован и изменялась лишь величина зазора, приведены в табл. 1. Данные показывают, что пьезокоэффициент вязкости начинает значительно влиять на пик давления только при очень малых зазорах ( h < 3∙10^–7). Влияние деформации упругой поверхности также становится выраженным лишь при малых зазорах.

Также рассмотрим влияние пьезоэффекта на пик давления в смазочном слое при фиксированном зазоре. Для этого выполним серию расчетов с разными значениями пьезокоэффициента. Согласно результатам расчетов, представленным в табл. 2, при значении α = 1,1∙10–8 1/Па влияние пьезокоэффициента на рост пика давления полностью компенсируется прогибом поверхности.

Далее проводим еще одну серию вычислительных экспериментов для нахождения коэффициента демпфирования λ с учетом влияния прогиба поверхности. Для этого рассчитаем величину несущей способности W для различных значений минимального зазора с учетом как положительных, так и отрицательных значений вертикальной скорости. При этом в каждом расчете используем итерационный метод. Зависимость несущей способности W от вертикальной скорости Vy показана на рис. 5. Зависимость контактной нагрузки от минимально зазора при нулевой вертикальной скорости показана на рис. 6.

Коэффициент демпфирования λ для различных значений минимального зазора определяется как тангенс угла наклона касательной к кривой, выражающей зависимость несущей способности W от нормальной скорости (рис. 5). Используя рассчитанный для различных значений h m массив значений λ и применяя сплайновую интерполяцию, определяем функцию λ( h m ), показанную на рис. 7. Также на рис. 7 показано изменение коэффициента демпфирования для аналитического решения (без учета деформаций и пьезоэффекта).

Найденные функции демпфирования и несущей способности подставляем в уравнение (13), выполняем численное интегрирование и получаем зависимость зазора от времени, а также из уравнения (7) находим соответствующие распределения давления в смазочном слое в различные моменты времени. На рис. 8 показан график изменения максимума давления с учетом коэффициента демпфирования и прогиба поверхности. На этом же рисунке для сравнения представлен аналогичный график максимума давления, полученный без учета пьезокоэффициента давления и прогиба поверхности. Расчет был выполнен для базового зазора 0,00000035 м.

Таблица 1

Минимальный зазор в смазочном слое hm , м	Максимальные P давление в смазочном слое
	Без учета пьезоэффекта и прогиба, 107 Па	Только с учетом пьезоэффекта, 107 Па	С учетом прогиба и пьезоэффекта, 107 Па
0,000001	1,26	1,33	1,23
0,0000005	3,59	4,18	3,48
0,00000035	6,13	8,2	5,6
0,00000025	10,02	19,1	8,37

Таблица 2

Пьезокоэффициент α, 10–8 1/Па	Максимальные P давление в смазочном слое
	Без учета пьезоэффекта и прогиба, 107 Па	Только с учетом пьезоэффекта, 107 Па	С учетом прогиба и пьезоэффекта, 107 Па
2,3	6,13	Нет решения	10,2
1,6		24,5	7,54
1,4		13,24	6,89
1,1		10,6	6,18
0,75		8,2	5,6
0,35		6,89	5,08

Максимальные давления в разных вариантах расчета (α = 0,75∙10^–8 1/Па, V_y = 0)

Влияние пьезокоэффициента на давление в смазочном слое ( h = 0,00000035 м, Vy = 0)

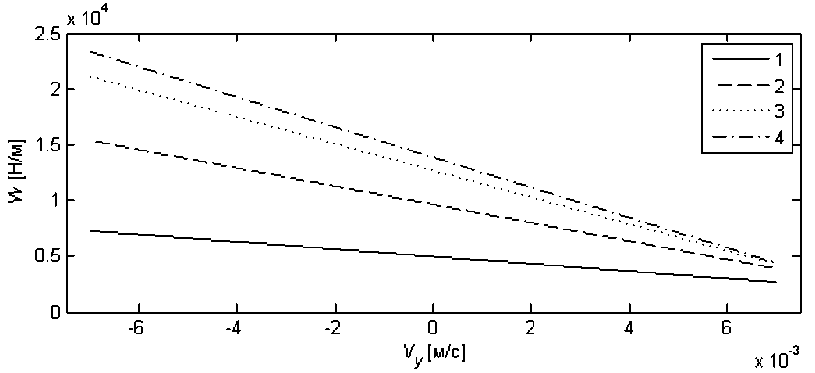
Рис. 5. Зависимость контактной нагрузки W от вертикальной скорости V_y :

1 – h = 0,000001 м; 2 – h = 0,0000005 м; 3 – h = 0,00000035 м; 4 – h = 0,00000025 м

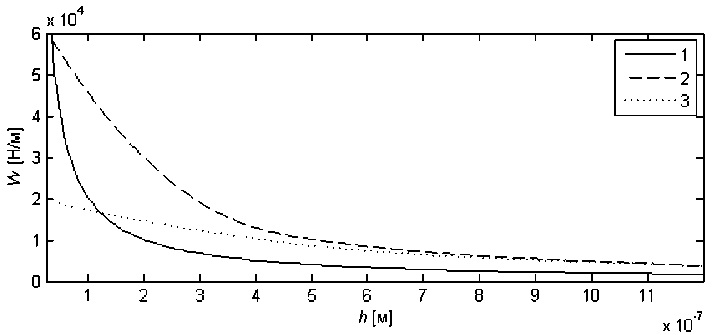
Рис. 6. Зависимость контактной нагрузки W от минимального зазора в смазочном слое h_m :

1 – аналитическое решение; 2 – с учетом только пьезоэффекта;

3 – с учетом прогиба поверхности и пьезоэффекта

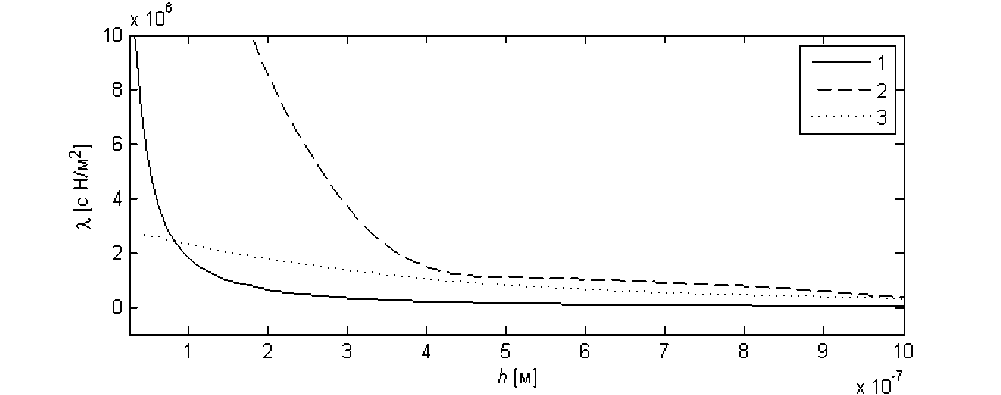
Рис. 7. Зависимость коэффициента демпфирования λ от минимального зазора h_m :

1 – аналитическое решение; 2 – с учетом только пьезоэффекта; 3 – с учетом прогиба поверхности и пьезоэффекта

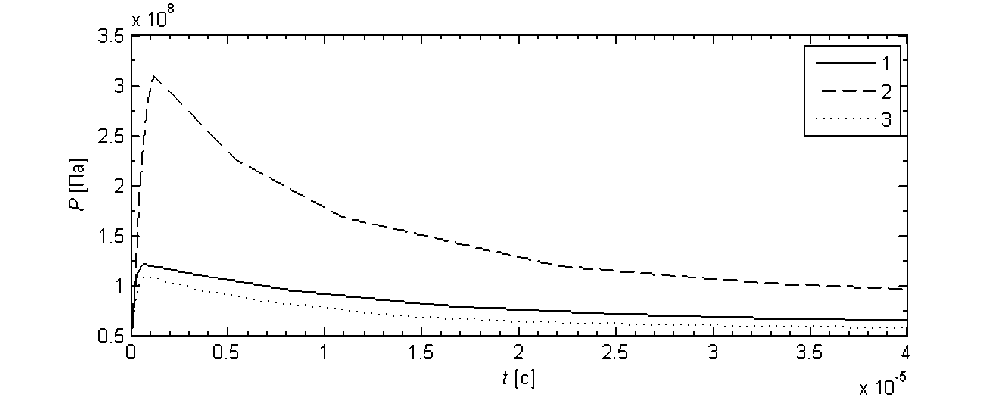
Рис. 8. Изменение пика давления в течение времени:

1 – аналитическое решение; 2 – с учетом только пьезоэффекта;

3 – с учетом прогиба поверхности и пьезоэффекта

Заключение. Решена задача нестационарного упруго-гидродинамического контакта ролика с пластиной с учетом прогиба поверхности, а также влияния давления на коэффициент вязкости. Для этого использовался разработанный ранее итерационный метод численного решения уравнения Рейнольдса совместно с интегральным уравнением связи прогиба поверхности с давлением в смазочном слое. В результате расчетов получены зависимости несущей способности и коэффициента демпфирования смазочного слоя от величины минимального зазора между роликом и пластиной. С использованием найденных функций изучен переходный процесс установления стационарного режима. Исследовано влияние пьезокоэффициента вязкости на пик давления, достигаемый в процессе установления. Найдено критическое значение пьезокоэффициента, при котором эффект возрастания давления, обусловленный увеличением вязкости, компенсируется влиянием деформации упругой поверхности.

Acknowledgements. The work was supported by grant of Russian Foundation for Basic Research 15-0508879.