Моделирование нестационарных процессов в газопроводах
Автор: Панферов Владимир Иванович, Панферов Сергей Владимирович
Рубрика: Инженерное оборудование зданий и сооружений
Статья в выпуске: 14 (86), 2007 года.
Бесплатный доступ
Рассматривается проблема моделирования переходных процессов в газопроводах, вызванных, в частности, резким закрытием регулирующего клапана. Методом Фурье найдены решения ряда задач. Приводятся результаты вычислений для конкретных эксплуатационных ситуаций.
Короткий адрес: https://sciup.org/147154161
IDR: 147154161 | УДК: 622.692.4
Текст научной статьи Моделирование нестационарных процессов в газопроводах
В.И. Панферов, С.В. Панферов
Рассматривается проблема моделирования переходных процессов в газопроводах, вызванных, в частности, резким закрытием регулирующего клапана. Методом Фурье найдены решения ряда задач. Приводятся результаты вычислений для конкретных эксплуатационных ситуаций.
В системах газоснабжения возникают ситуации, когда по какой-либо причине тот или иной регулирующий орган достаточно быстро закрывается. Понятно, что это приводит к возникновению переходного процесса, в водяных тепловых сетях, например, это действие является совсем небезопасным и часто сопровождается таким явлением как гидравлический удар. Поэтому представляет интерес вопрос о том, что конкретно произойдет в этом случае в газопроводе, как, в частности, будет изменяться давление в различных точках по его длине. Кроме того, в аварийных ситуациях возможно появление импульса высокого давления из магистрального газопровода и ряд других событий. Во всех этих случаях в газопроводах возникают нестационарные процессы. В связи с этим в работе рассматривается несколько задач моделирования переходных процессов в системах газоснабжения.
Известно [1-5], что нестационарное течение газа в газопроводе удовлетворительно может быть описано следующей системой уравнений в частных производных:
, 9х 9т 2d (|)
. 9т Эх где Р(х,т), р(х,т), w(x,t) - соответственно давление, плотность и скорость течения газа в точке х по длине газопровода в момент времени т ; X -коэффициент гидравлического трения; d - внутренний диаметр газопровода; с - скорость звука в газе; L- длина рассматриваемого участка газопровода.
Установлено [1 и др.], что для длинных газопроводов и в случае больших потерь на трение математическую модель (1) можно упростить, от-
Э^р ■ w) брасывая член ------. Кроме того, модель мож-
9т но дополнительно линеаризовать, полагая, что W
Л—= £=const, тогда нестационарный процесс в 2d газопроводе будет описываться следующей системой уравнений:
_^——lX=,K.р(^х^
■ w(x,t\0
< (2)
9P^x,t^ 2 5(p(^,t)-w(x,t))
--------= С -----------------, U < X < L, Г > и.
. 9т 9х
Нетрудно видеть, что переменные р(х,т) , w(x,t) могут быть исключены из рассмотрения и в этом случае давление Р(х,т') должно удовлетво рять следующему уравнению:
9Р(х, т) _ с" 92Р(х,т)
9т к Эх2 ’ поэтому в целом задача, когда считается, что в любом режиме давление начале участка поддерживается автоматическим регулятором на одном и том же уровне Ро, а в конце этого участка регулирующий клапан мгновенно закрывается, формально записывается так:
9Р(х, т) _ с2 92Р(х,т)
Для приведения задачи к решаемому виду введем переменную 6(х,т)=Р(х,т)-Р0 , тогда, как это нетрудно видеть, задача перепишется следующим образом:
??^=£tf*Kli()<;t
дт к дх"
в(х,О)=Дх)-Ро,О<х<Ь;(8)
6(0,т)=0, г>0;(9)
^2=0, т>0.(10)
Эх
Решая задачу (7)—(10) методом разделения переменных, найдем, что еДтД^А^етД- —-)sm(^x),(11)
2 L где 4 =-■ f[/(x)-Poising,х)г ц,= ^--(2/-1).
L о
Известно [6], что в стационарном режиме давление по длине газопровода распределяется по параболе, однако, как это достаточно хорошо известно, это распределение на практике удовлетворительно может быть аппроксимировано прямой, поэтому при моделировании полагали, что Р^-Рд-^-х, (12)
где Д давление в точке х = L в начале процесса.
В этом случае
(P1-P0)sin(^,Z,) .
Под
черкнем, однако, что условия (5) и (12) означают, что рассматривается задача, когда переходный процесс обусловлен только закрытием клапана в конце газопровода, давление в его начале, каким оно было в стационарном режиме, таким оно остается и в последующие моменты времени.
На рис. 1 приведены кривые изменения давления по длине газопровода: кривая 1 - для г = 0, кривая 2 - для г = 1, кривая 3 - для для г = 2, кривая 4 - для г = 3 с, при этом L = 1800м, d = 0,325мм, 2 = 0,013, с = 451м/с, Л: = 0,176с ’, PQ =6 ■ 105 Па, Д =5,7 ■ 105 Па . Значение коэффициента к вычислялось в соответствии с рекомендациями работы [1 и др.].
На рис. 2 приведены кривые изменения давления во времени в конце - кривая 1 и в середине газопровода - кривая 2.
Как видно из рис. 1 и 2, переходный процесс имеет апериодический характер, никаких «выбросов» давления в данном случае не наблюдается.
Теперь рассмотрим следующую задачу: будем полагать, что в момент времени г = 0 закрывается клапан в конце участка, а в его начале давление скачком поднимается до уровня в магистральном газопроводе /^. В этом случае задачу следует перерешать при условии, что Р^тДР^д = const, т>0, начальное распределение давления остается прежним и описывается уравнением (12). Формула для вычисления 4 будет уже такой
4 =-2^№ -P0)sin(M)+—7(^0 -^мг),
А I а в целом давление в любой точке газопровода в любой момент времени будет вычисляться по следующему соотношению:
Р^хД =PW + £4 -ехр(-^-—)-sin(^x).(13)
к
На рис. 3 приведен график изменения давления во времени в конце указанного газопровода - кривая 1 и в его середине - кривая 2 при До- = 4 МПа .
Как видно из рис. 3, переходный процесс также имеет апериодический характер, давление во всех точках газопровода плавно поднимается до уровня Рю.
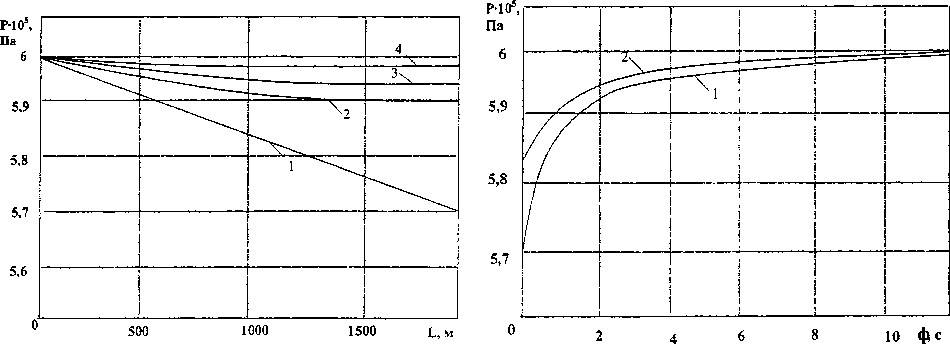
Рис.2. Кривые изменения давления во времени в конце и в середине газопровода
Рис.1. Распределение давления по длине газопровода в различные моменты времени
Инженерное оборудование зданий и сооружений
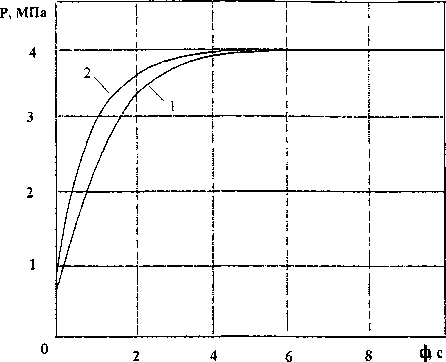
Рис. 3. Кривые изменения давления во времени в конце и в середине газопровода при Рмг=4 МПа
До сих пор мы полагали, что рассматриваемый газопровод можно отнести к категории длинных газопроводов или же потери на трение достаточно велики. Рассмотрим теперь другой предельный случай, когда газопровод короткий или потери на трение достаточно малы. В этом случае в исходной системе уравнений (1) инерционный
8(p-WA „ член ------ следует оставить, a л-— можно
8т 2d отбросить [1 и др.], тогда нестационарный процесс в газопроводе будет описываться следующей системой уравнений:
8Р(х,т^ З^х^У^т))
--=----------------, и < х < L, г > 0;
8Р(х, г) 2 3(р(х, т) ■ и<х, г))
— ----— С -------------<х
. 8т Эх
Нетрудно видеть, что переменные /?(х,т), w(x,r) также могут быть исключены из рассмот рения и в этом случае давление должно удовлетворять следующему уравнению:
82Р(х,т)_ 2 32Р(х,т)
дт2 8хг поэтому в целом задача, когда считается, что в любом режиме давление начале участка поддерживается автоматическим регулятором на одном и том же уровне Во, а в конце этого участка регулирующий клапан мгновенно закрывается, будет представляться следующей системой уравнений: f^ = ^^2,0
5г25х
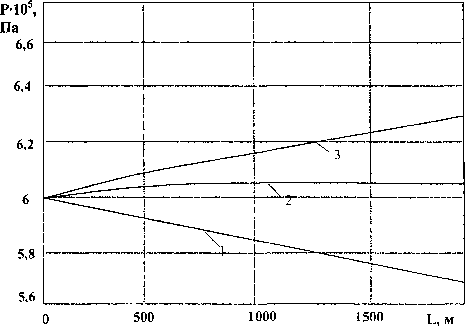
/’(x,0)=/(x),0 ^^ = 0, 0 8т P(0,t) = Pq =const, т>0; ^^=0,г>0;(19) 8х Здесь процесс описывается уже волновым уравнением с соответствующими начальными и граничными условиями, причем условие (17) означает, что в начальный момент времени в любой точке по длине газопровода скорость изменения давления во времени равна нулю, что вполне соответствует действительности. Решая задачу (15)—(19) методом Фурье, нашли, что Р(х,г)=Ро+2уРх-РУ)^8^^ х COS^C----217—"S™^ /2 • (2z -1) • x/Z). (20) На рис. 4 приведены кривые изменения давления в конце - кривая 1 и в середине газопровода -кривая 2 при Ро=6 1О5Па и Р]=5,7 105Па для модели (15)—(19). Как видно из рис. 4, процесс, как и следовало ожидать, колебательный, причем наибольший «выброс» давления наблюдается в конце газопровода и он равен 6,3 ■ 105 Па . На рис. 5 показано, как распределяется давление по длине газопровода в различные моменты времени при описании явления волновым уравнением: кривая 1 для г = 0с, кривая 2 для г=5с, кривая 3 для т =8 с . Рис. 4. Волновой процесс изменения давления во времени в конце и в середине газопровода Рис. 5. Изменения давления по длине газопровода в волновом процессе Понятно, что реальный процесс занимает промежуточное положение между двумя рассмотренными предельными случаями. Поэтому, учитывая полученные результаты, достаточно обоснованно можно заключить, что реальный переходный процесс, обусловленный закрытием клапана в конце газопровода, очевидно, имеет вид затухающих колебаний, наибольшая амплитуда колебаний наблюдается непосредственно у самого клапана, однако увеличение давления не столь большое, как это имеет место при гидравлическом ударе в капельной жидкости.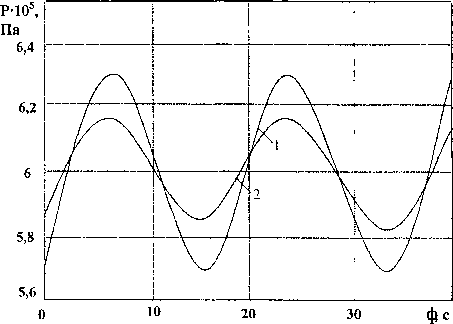
Список литературы Моделирование нестационарных процессов в газопроводах
- Чарный И.А. Основы газовой динамики/И.А. Чарный. -М.: Гостоптехиздат, 1961. -196 с.
- Галиуллин З.Т. Интенсификация магистрального транспорта газа/З.Т. Галиуллин, Е.В. Леонтьев. -М.: Недра, 1991. -272 с.
- Баясанов Д.Б. Автоматизированные системы управления трубопроводными объектами коммунального хозяйства/Д.Б. Баясанов. -М., Стройиздат, 1974. -312 с.
- Юсубов Ч.А. Численное определение нестационарных процессов в магистральных газопроводах/Ч.А. Юсубов//Проблемы энергетики. -2003. -№ 2. -С. 62-65.
- Поляков Г.Н. Моделирование и управление газотранспортными системами/Г.Н. Поляков, Е.И. Яковлев, А.С. Пиотровский. -СПб.: Недра, 1992. -256 с.
- Бобровский С.А. Гидравлический расчет распределительных трубопроводов/С.А. Бобровский. -М.: Стройиздат, 1968. -159 с.


