Моделирование объема пиломатериалов с учетом сбеговой зоны ствола

Анализ структуры лесопиления в России показывает, что доля отходов достигает 45 % [6], поскольку неизменной остается геометрия раскроя бревна. Только около четверти этих отходов используется как вторичное сырье для производства различных видов продукции, чаще всего технологической щепы. Другие направления использования отходов мало распространены из-за высокой стоимости оборудования и зачастую высоких требований к сырью. Например, производство топливных брикетов или гранул требует опилок с влажностью не более 12 %, однако сушильными камерами обладают далеко не все лесозаводы. Из оставшихся на выходе 55 % полезной пилопродукции часть отбраковывается из-за пороков древесины или по причине технического брака. Бревна малых диаметров (12-14 см) из-за низкого выхода пиломатериалов традиционного сечения пока еще не находят должного применения в лесопилении. По этой причине стоимость кубометра тонкомерных бревен в 1,5-2 раза ниже, что делает их потенциально привлекательными для переработки.

Одним из путей повышения объемного выхода продукции является снижение потерь древесного сырья за счет использования так называемой сбеговой зоны бревна. Под сбеговой зоной понимается боковая часть бревна, при продольном раскрое которой длина полученных пиломатериалов меньше длины исходного бревна. (Пиломатериалы, имеющие длину исходного бревна, получаются из так называемой пифаго-рической зоны.) Возможны два основных направления использования древесины из сбего-вой зоны: непосредственная выработка деталей © Питухин Е. А., Чикулаев П. С., 2011

из отходов или рациональный выбор сечений пиломатериалов. Полезный выход при первом способе составляет всего 20-30 % от объема отходов на входе при значительных материальных затратах [4].

В этой связи большой интерес представляет использование сырья, полученного вторым способом, для дальнейшей переработки на клееные щитовые заготовки различных габаритов. Рассмотренные далее заготовки позволят повысить объем полезной продукции предприятий, занимающихся производством клееных конструкций. При рассмотрении прочностных характеристик этих конструкций было выявлено, что они не уступают соответствующим характеристикам цельной древесины и зачастую их превосходят. При этом по удельной прочности (отношению прочности к удельному весу) клееная древесина не уступает стали [8].

На рис. 1 представлена принципиальная схема формирования клееных щитов из заготовок различной формы. Данные заготовки получаются обрезкой необрезных досок вдоль их кромок, поэтому на виде сверху они имеют форму трапеции. При склейке в щит заготовки складываются попеременно вершинными и комлевыми торцами, чтобы компенсировать сбег. Под сбегом понимается изменение диаметра бревна (в сантиметрах), приходящееся на 1 м его длины.

Целью статьи является оценка возможного прироста полезного выхода пилопродукции при переходе на нетрадиционные сечения и разработка моделей, позволяющих производителю определить оптимальные параметры заготовок для своих условий. Для достижения данной цели предлагается провести имитационное моделирование [2] объемов заготовок различных форм, что позволит заранее оценить результат применения той или иной технологии в процессе реального производства заготовок из бревен.

^a opt

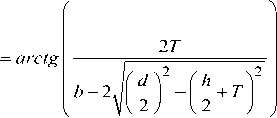
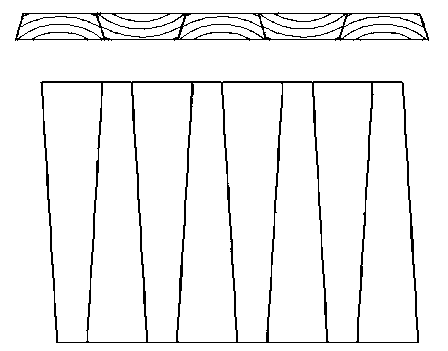
Рис. 1. Схема склейки трапецеидальных заготовок

Примем за L длину бревна, за Sb - сбег бревна. Тогда объем одной заготовки с трапецеидальным сечением и пластью определяется по фор-

муле:

при

trap ₂

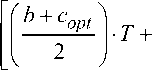
¹ B+c^'

D = d + Sb • L .

• T

• L ,

этом b = 2

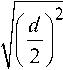
B = 2

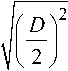
На основе результатов проведенного вычислительного эксперимента, с учетом сформированных количественных и качественных требований к характеристикам заготовок могут быть сделаны общие выводы о том, насколько каждый из видов заготовки эффективен с точки зрения итогового объемного выхода.

На рис. 2 представлено поперечное сечение пары заготовок с трапецеидальными пластью (плоскостью доски, получаемой в результате пропила) и сечением.

Вершинный торец              Комлевой торец

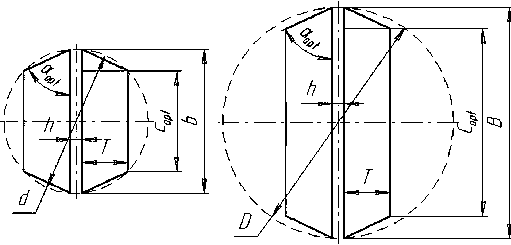
Рис. 2. Сечения заготовки с трапецеидальной пластью и сечением в вершинном и комлевом торцах: d - вершинный диаметр исходного бревна; D - комлевой диаметр исходного бревна; T - толщина заготовки; h - величина пропила; b - ширина внутренней пласти заготовки в вершинном торце; B - ширина внутренней пласти заготовки в комлевом торце; c opt - ширина наружной пласти заготовки в вершинном торце; C opt - ширина наружной пласти заготовки в комлевом торце; a opt - оптимальный угол наклона кромки заготовки к пласти, обеспечивающий максимальный объемный выход при заданной толщине заготовки и диаметре бревна, 2 T

При имитационном моделировании процесса моделируемая характеристика должна зависеть от случайных параметров.

Пусть d - случайная величина в пределах диапазона [d_mn;d_ma^, закон распределения которой будет определен ниже; d min и d_max - соответственно минимальный и максимальный вершинные диаметры бревен в партии.

Поскольку приемка пиловочника ведется только по верхнему диаметру, сбег никогда не измеряется. В модели его можно задать как случайную величину с допущением о равномерном законе распределения сбега в пределах, общеизвестных для хвойных пород [1], [5].

Пусть Sb - случайная величина, равномерно распределенная по интервалу [ Sb 0 ; Sb 0 +ASb ], где Sb 0 - минимальный сбег бревен в партии, а ASb -модуль максимального отклонения сбега от минимального.

Учитывая, что C opt = B - b + c opt , запишем выражение (2) в виде следующей функциональной зависимости:

2 \2 772 2

I d I I ^h I I d ^{+ Sb} ■ ^L I I h I

Vt rap⁽ d , ^Sb ) = T • ^L • JI у I ^— I 2 ⁺ T I ⁺J I — 2— I ^— I 2 ) ' (3)

С

связанный соотношением tg a opt = ь

—

c opt

учетом того что c_opt

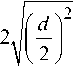
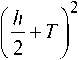
Выражение (3) представляет собой стохастическую модель определения объема заготовки с трапецеидальным сечением и пластью в зависимости от двух случайных величин d и Sb .

Рассмотренное выше трапецеидальное сечение имеет один технологический недостаток: при склейке заготовок в щит возможно смещение (выдавливание) заготовок друг относительно друга. Данной проблемы можно избежать, если использовать пресс с вертикальным прижимом. Если такой возможности нет, целесообразно получение заготовок со ступенчатым сечением, представленным на рис. 3.

Под количеством ступенек понимается минимальное количество прямоугольников, на которое можно разбить данное ступенчатое сечение (в данном случае их 3). Для обеспечения воз-

можности склейки заготовок необходимо, чтобы количество ступенек, а также их ширина и высота были одинаковы.

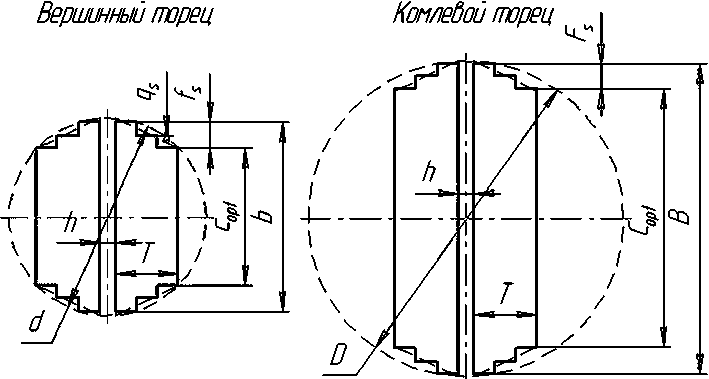
Рис. 3. Сечения заготовки со ступенчатой кромкой в вершинном и комлевом торцах ( q s — ширина ступеньки)

Объем трапецеидальной заготовки со ступенчатым сечением рассчитывается как сумма объемов досок, соответствующих каждой ступеньке:

n

Vste„ = У T ■ -21 Л + CjOPt- 1+21 Л + Copt-1 , (4) step                        s j                    s j j=1L k 2 L V 2 J V 2 JJJ где k — количество ступенек в сечении; j — порядковый номер ступеньки; fs. — величина, показывающая, насколько половина ширины каждой ступеньки превышает половину ширины наружной пласти заготовки, и определяемая по следующей формуле:

—

hT

+--

2 k

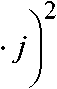
c opt

С учетом (4) и (5) итоговая стохастическая модель для вычисления объема заготовки со ступенчатым сечением и трапецеидальной плас- тью принимает вид

У_яер ( d , Sb ) = £ j

T ■ L f f d ) ² ( h T      |( d + Sb ■ L ) ² ( h ) ²   f d ^T h )²

2,      —  +—■ j +            —     —      — k I К2J  V2 k К 2 J  V2J  Я 2 J  V2)

В условиях реального производства речь идет не о единичных бревнах, досках или заготовках, а о партиях. Для каждого бревна в партии максимальный объем модели трапецеидальной заготовки выходит, когда кромка заготовки в вершинном торце лежит на образующей бревна. В отличие от этого, объем модели заготовки со ступенчатым сечением зависит не только от геометрии бревна, но и от количества ступенек. Алгоритм для определения максимального из возможных объемов партии ступенчатых заготовок представлен в виде блок-схемы на рис. 4. Используя данный алгоритм, производитель может определить объем партии таких заготовок, задав только количество и длину бревен, максимальный и минимальный диаметр бревна в имеющейся партии, толщину досок и количество ступенек в сечении.

Исходными данными алгоритма являются длина и количество бревен в партии, а также ми- нимальный и максимальный вершинный диаметры бревен в партии. Длина всех бревен в партии принимается одинаковой. Толщина заготовки T выбирается производителем в зависимости от требуемой толщины клееного щита на выходе.

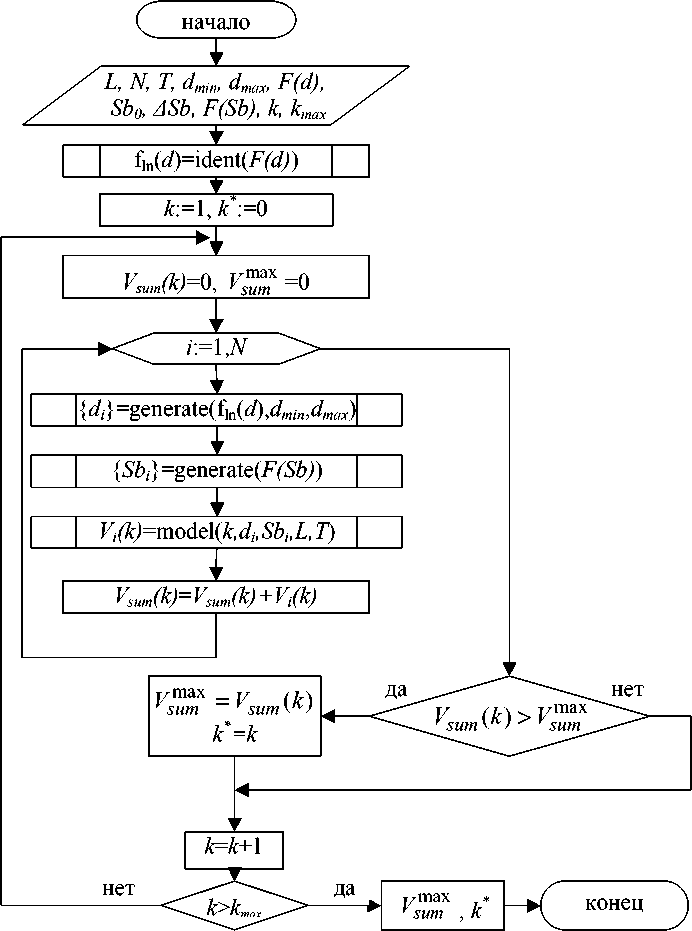
Рис. 4. Блок-схема алгоритма вычисления максимального объема партии заготовок со ступенчатым сечением: N — количество бревен; d min и d max — минимальный и максимальный вершинный диаметры бревен в партии; F(d) — выборка, состоящая из реализаций вершинных диаметров бревен в партии, полученная в результате натурного эксперимента; F(Sb) — равномерный закон распределения сбегов бревен в партии; i — номер бревна; f_ln( d ) = ident( F(d)) — модуль идентификации параметров теоретического распределения вершинных диаметров бревен; V_sum(k) — суммарный объем партии заготовок со ступенчатым сечением; generate(f_ln( d ), dmin , d max ) — пользовательская функция, реализующая случайный вершинный диаметр в диапазоне от d_min до d_max в соответствии с идентифицированными параметрами теоретического закона распределения; generate( F(Sb) ) — пользовательская функция, реализующая случайный сбег; к — количество ступенек; k max — максимальное технологически приемлемое количество ступенек; к* и V™^x— оптимальное количество ступенек и соответствующий ему максимальный объем пар ти и заготовок; V_sum(k) — суммарный объем партии заготовок с количеством ступенек к ; model( k,d,,Sb,,L,T) — математическая модель (6), определяющая объем заготовки с количеством ступенек k в сечении

При приемке диаметр каждого бревна, как правило, измеряется индивидуально, но вводить все диаметры каждой поступающей на предприятие партии бревен в математическую модель нецелесообразно из-за неоправданных временных затрат. В данном случае следует задаться наиболее подходящим теоретическим законом распределения диаметров бревен в партии, определенным на основе некоторой экспериментальной выборки.

Для определения закона распределения вершинных диаметров бревен в партии [9] были собраны и обработаны статистические данные о партиях бревен, поступающих на петрозаводский ДОК.

Проверялось соответствие экспериментальных данных теоретическим законам распределения Вейбулла, Гамма-распределения, распределения Гумбеля (экстремального закона) и логнормального закона (рис. 5). После статистической проверки гипотезы о соответствии теоретического закона экспериментальным данным с помощью непараметрических критериев Колмогорова - Смирнова [10] и ш ² (омега-квадрата) Мизеса [7] в конечном итоге был принят логнормальный закон распределения диаметров как учитывающий специфику распределения продолжительности жизни биологических объектов [3].

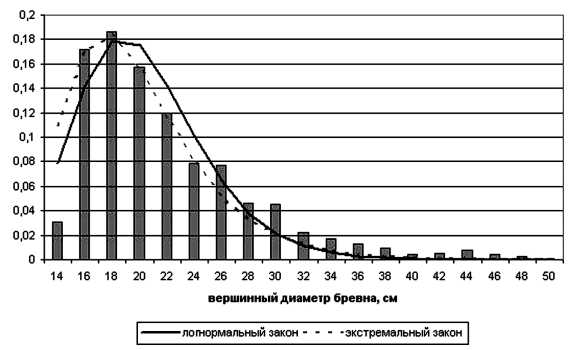
Рис. 5. Результаты подгонки логнормального и экстремального законов к гистограмме распределения вершинных диаметров бревен

Поскольку реальный диаметр бревна не может быть бесконечно малой или большой величиной, логнормальный закон распределения диаметров бревен должен иметь усеченный вид.

В связи с тем что рассматриваемая технология ориентирована в первую очередь на тонкомерные бревна, в том числе на их вершинные части, было решено принять за минимальный сбег в партии бревен так называемый нормальный сбег (он равен 1 см/м) [1], [5], максимальное отклонение от нормального принято равным 15 %.

В ходе реализации имитационного моделирования по методу Монте-Карло была сгенерирована партия из 10 000 бревен, что соответствует месячному объему переработки среднего лесоперерабатывающего предприятия, со следующими параметрами: длина - 6 м, вершинные диаметры - от 12 до 30 см, сбеги - от 1,00 до 1,15 см/м. Математическое ожидание и СКО диаметров составили соответственно 21 и 3 см. Толщина получаемых заготовок принята равной 50 мм, а пропил - 4 мм.

С использованием стохастической модели (3) вычислен объем партии заготовок с трапецеидальным сечением. Алгоритм вычисления максимального объема партии таких заготовок аналогичен алгоритму, приведенному на рис. 4, с той разницей, что результатом его работы вместо оптимального количества ступенек является оптимальный угол наклона кромки заготовки к ее пласти для всей партии бревен. При этом получена зависимость индивидуального оптимального угла наклона кромки заготовки к ее пласти, представленная на рис. 6, которая иллюстрирует выражение (1). Для данной партии индивидуальные оптимальные углы, округленные до целых значений, лежат в пределах 59- 79 ° .

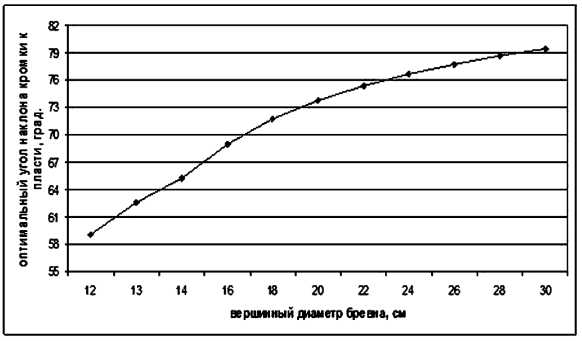
Рис. 6. Зависимость индивидуального угла наклона кромки к пласти для заготовки с трапецеидальным сечением и пластью

Поскольку невозможно склеивать трапецеидальные заготовки с разными углами наклона кромки к пласти, был определен единый для всей партии угол, который обеспечивал бы максимальный объемный выход всей партии. Для этого при переборе всех вариантов углов (21) было установлено ограничение на брак: если общий для партии угол оказывался больше индивидуального, то объем данной заготовки не учитывался в сумме, так как она имеет брак (обзол). На рис. 7 представлена зависимость объемного выхода партии трапецеидальных заготовок от единого для всей партии угла наклона кромки заготовки к пласти. При этом максимум приходится на 62 ° , что на 3 ° больше минимального из углов в партии. Это объясняется тем, что на первоначальном этапе роста угла выигрыш от увеличения угла на бревнах больших диаметров превосходит потери из-за образования брака на бревнах меньших диаметров. Однако разница максимального объема с объемом, соответствующим наименьшему в партии углу, пренебрежительно мала, что позволяет рекомендовать при выборе единого для партии угла а остановиться на его минимальном значении. То есть производителю следует определить угол а для бревна с наименьшим диаметром в партии по формуле (1) и принять его для всей партии.

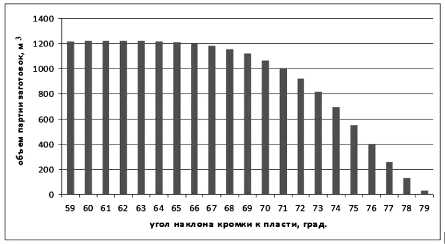
Рис. 7. Зависимость объемного выхода партии трапецеидальных заготовок от единого угла наклона кромки к пласти

С использованием модели (6) и алгоритма, изображенного на рис. 4, определены объемы заготовок с количеством ступенек в сечении от 1 до 9. Зависимость итогового объема от количества ступенек показана на рис. 8. Максимальное технологически приемлемое количество ступенек для толщины заготовки 50 мм с точки зрения удобства изготовления и эксплуатации режущего инструмента не превышает к = 5, поэ- max тому принимаем к = 3.

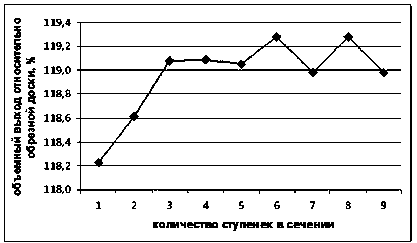
Рис. 8. Зависимость объема партии ступенчатых заготовок от количества ступенек

В таблице приведены итоговые объемы партий рассмотренных заготовок относительно рассчитанного объема партии обрезных досок.

Относительные объемы партий заготовок различных сечений

Вид заготовки	Объем относительно обрезной доски
Заготовка с трапецеидальным сечением и пластью	120,4 %
Заготовка со ступенчатым сечением (3 ступеньки) и трапецеидальной пластью	119,1 %

Как видно из таблицы, прирост объема относительно традиционной обрезной доски при смене сечения и пласти на трапецеидальные составляет 20,4 %. Объем заготовок со ступенчатым сечением и трапецеидальной пластью меньше на 1,3 %. Учитывая незначительную разницу в объемах, при выборе между этими сечениями стоит исходить в первую очередь из технологических особенностей предприятия. Таким образом, рассматриваемый способ получения заготовок позволяет увеличить итоговый полезный выход пиломатериалов с 55 до 66 % от объема исходного сырья.

Итак, на основе разработанных стохастических моделей объемов заготовок различной геометрической формы и найденного вида закона распределения вершинного диаметра исходного сырья был проведен вычислительный эксперимент на основе методов имитационного моделирования, который позволил определить оптимальные геометрические параметры заготовок с точки зрения получения максимального объемного выхода пилопродукции и удобства их дальнейшей обработки. Разработанные модели позволят производителям определить наиболее подходящие им параметры заготовок в зависимости от технологических ограничений, имеющихся партий пиловочника и параметров заготовок на выходе.