Моделирование образования кластеров в сплавах на основе Fe-Cr

В последние годы существенно возрос интерес к исследованию различных свойств хромосодержащих сталей как одних из наиболее перспективных материалов атомной техники [1, 2]. Данный вид сталей, как правило, характеризуется высокой степенью устойчивости к радиационному распуханию при сохранении пластичности в условиях реакторного облучения. Данные свойства обычно связывают с образованием в них -фазы, которая представляет собой кластеры, в основном состоящие из атомов хрома [3-5].

Важной особенностью - фазы в сплавах на основе системы железо-хром является ее заметное обогащение атомами железа по сравнению с макроскопическими выделениями. Эта особенность наблюдалась экспериментально как в процессе термического отжига [5], так и под облучением [6] и может быть объяснено влиянием энергии межфазной границы на составы сосуществующих фаз [7, 8]. Это влияние становится особенно заметным в случае наноразмер-ных кластеров и может приводить к изменению составов фаз в несколько раз. С учетом данного обстоятельства удается построить модель [7] на

основе известных методов кинетики квазимоле-кулярных реакций (см. например, [9]), что позволило удовлетворительно описать кинетику образования кластеров в условиях термического отжига в сплаве Fe-20%Cr при температуре T = 773 K [7].

При облучении сплавов в реакторах происходит многократное повышение концентрации радиационных дефектов [10, 11]. Если предположить, что процесс диффузии атомов сплава происходит по D_Cr = 1.4 X 10 ¹⁹ cm 2 / 5 вакансион-ному механизму, то можно ожидать резкого увеличения скорости диффузионных процессов (пропорционально концентрации вакансий), а соответственно и радиационно-стимулированного образования кластеров, которое наблюдалось экспериментально [6, 11].

В данной работе предполагается рассмотрение a' — фазы в сплавах Fe-Cr в условиях облучения на основе разработанной модели образования и роста кластеров в условиях термического отжига [7]. Для решения этой задачи необходимо определить влияние радиационных дефектов, образующихся в условиях реакторного облучения, а также оценить изменение коэффициента диффузии и степени пересыщения твердого раствора под действием облучения.

• 2.    ФАЗОВЫЙ СОСТАВ СПЛАВА FE-CR, СОДЕРЖАЩИЙ НАНОРАЗМЕРНЫЕ КЛАСТЕРЫ

Рассмотрим бинарный сплав Fe-Cr, в котором произошло образование кластеров. Пусть кластеры имеют сферическую форму и в общем случае могут содержать произвольное количество атомов хрома и железа. Для учета особенностей кристаллической решетки, а также установления связи между радиусом кластера R и количеством атомов обоих сортов удобно пользоваться соотношениями, обычно применяемыми для анализа кластерных систем:

R = a ( w + y )^1/3, a

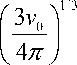
NS = b (w + y )2/3.          (1)

Здесь v ₀ - объем, занимаемый одним атомом, b – параметр, зависящий от типа кристаллической решетки, w и y – количество атомов хрома и железа в кластере соответственно.

Будем считать, что образующиеся кластеры являются когерентными решетке матрицы, тогда энергия границы раздела в приближении регулярных растворов [12] имеет вид [7, 13]:

0           1           2           3           4           5

Cluster radius, nm

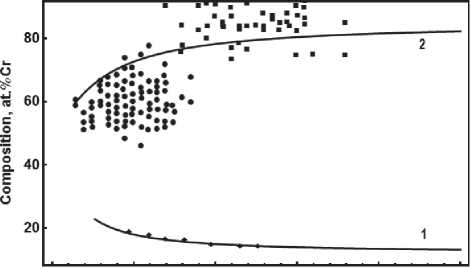
Рис. 1. Зависимость фазового состава сплава Fe-Cr от радиуса кластера при температуре 773K.

Сплошные линии результат моделирования:

1 - состав матрицы, 2 - состав кластеров. Точками отмечены экспериментальные данные [5]:  – состав матрицы в зависимости от среднего радиуса кластеров (для разных продолжительностей отжига 501067 ч), – состав кластеров в зависимости от радиуса (после отжига в течение 50часов); – состав кластеров в зависимости от их радиуса (после отжига в течение 1067 часов)

G S = zb Q ⁽ w ⁺ y^)2/ 3 ( x " _ x P ) ² ,    (2)

z где Q = -(2EaB

— E BB — E AA ) - параметр квази-

химического взаимодействия, выражаемый через энергии парного взаимодействия между атомами E , E , E„ „, z„ - количество связей атомов AB AA BB S кластера с атомами матрицы. В работах [7, 8]

установлено, что соотношение параметров z S b / z для объемно-центрированной кубической решетки имеет значение 1.318 ± 0.004 .

Рассмотрение задачи об определении фазового состава бинарного сплава, в котором произошло образование кластеров, может быть проведено с помощью формул [7]:

соответственно. Полученный результат достаточно хорошо согласуются с экспериментальными данными по растворимости атомов хрома в альфа-железе и атомов железа в хроме, приводимыми другими авторами [5].

¹ — x C, = X P ( ^Т ) ex_p ( _— ² z s ba _ г

1 — x ^, X “e ( Т ) p ( 3 zkTR ^[ C^,

— x ^, ] ■ Г x p, + 2 x C, ]) ,

x

a

Cr

x

P

Cr

X“c ( T ) X P ( T )

exp

( 2 z_Sba 1 3 zkTR

^ [ x C,

^^^^^B

xCr

,

где введено обозначение: X* ( T ) - концентрация атомов сорта n ( п = { Fe , C, } ) в i -фазе для макроскопических выделений (т.е. соответствующая пределу R ^ ^ ).

С помощью системы уравнений (3) удалось достаточно хорошо описать зависимость фазового состава для сплава Fe-Cr в зависимости от размера частиц второй фазы (рис. 1). Параметр ква-зихимического взаимодействия Q может быть определен с помощью результатов расчета энтальпии смешения ^ H mix бинарного разупоря-доченного сплава Fe-Cr полученных в работе [14]: Q = 4 N H_mix ~ 0.4 eV . При расчетах варьировались значения предельных концентраций X Cr и X F?_e , которые оказались равными 12 и 85at.%

3. МОДЕЛИРОВАНИЕ КИНЕТИКИ ОБРАЗОВАНИЯ КЛАСТЕРОВ В СПЛАВЕ

FE-CR В ПРОЦЕССЕ ТЕРМИЧЕСКОГО ОТЖИГА

Рассмотрим пересыщенный твердый раствор Fe-Cr, содержащий атомов хрома, находящийся при постоянной температуре T . Пусть в процессе распада данного твердого раствора в процессе термического отжига образуются кластеры сферические кластеры. Состав кластеров будем считать квазиравновесным, т.е. в каждый момент времени состав кластеров определяется их радиусом в соответствии с рис.1. Такое предположение является справедливым, если диффузия железа внутрь кластеров осуществляется заметно быстрее, чем происходит присоединение атомов хрома к кластерам.

Предположим, что рост кластеров связан с диффузионным присоединением атомов хрома к кластерам, тогда количество атомов хрома в кластерах может быть определено с помощью известного соотношения [15]:

dw = 4^DC,R dt v     (xC,(t) xC,(R)),      (4)

где x_C , ( t ) - концентрация атомов хрома в мат-

рице в момент времени t , xC, ( R ) - равновесная концентрация атомов хрома в альфа-железе над искривленной поверхностью кластера, определяемая с помощью (3), D Cr – коэффициент диффузии хрома в альфа-железе при рассматриваемой температуре T .

Поскольку при моделировании необходимо одновременно рассматривать кластеры, количество атомов в которых может изменяться в достаточно широких пределах, целесообразно перейти от числа атомов хрома в преципитатах w к величине r , определяемой соотношением:

/ \ з f r 1

w = HI . (5) V a J

Новая переменная r имеет тот же порядок, что и радиус кластера R , и соответствует эффективному радиусу, который имел бы кластер, состоящий только из атомов хрома. Поскольку, в соответствии со сделанными предположениями, состав кластеров зависит только от их размера, то связь между параметром r и радиусом R может быть определена с помощью формулы:

R =

r

( Xc_r H .

Подстановка уравнения (6) в (5) приводит к следующему соотношению для скорости изменения величины :

dr =  DCr dt  r (xC^^

( x Cr ⁽ t ) - x ^C r ^{( r} ) )

При этом равновесные составы фаз X C . ( r ) и Xcr ( r ) , выраженные в атомных долях, могут быть установлены с помощью рис. 1 и системы уравнений (3) и (6).

Обозначим С ( r , t ) концентрацию кластеров, характеризуемых параметром r в момент времени t . Предположим, что в процессе отжига образуются зародыши, характеризуемые значением r = r ₀ , при этом скорость изменения концентрации зародышей может быть описана формулой:

C ^0, t ) = G ( ^X C ⁽ t ) ^{- X} Cr ⁽ r ) ) ^- k ^r o ^{) C ( r} o , t ) ^X Cr^{( t} ) ⁺ C t         ^x

⁺ g ^r 0 ^{+ S r ) C}r ^{+S r} , t ),             (8)

где введен параметр генерации G , определяющий скорость зарождения и распада критических зародышей размера r ₀ , и введен шаг S r изменения параметра r для рассматриваемого ансамбля кластеров, k ( r ) и g ( r ) - кинетические коэффициенты характеризующие вероятность изменения параметра r в единицу времени.

Скорость изменения концентрации кластеров С(r, t) , характеризуемых параметром r , может быть определена с помощью кинетическо го уравнения:

дС ⁽ г , t ) = k ( r - g r ) c ( r - S r , t ) x C ( t ) + g ( r + S r ) C ( r + S r , t ) - C t

-(k(r)x“cr(t) + g(r))c(r, t).(9)

Кинетические коэффициенты k ( r ) и g ( r ) могут быть легко определены с помощью уравнений (3), (6), (7):

k ⁽ r ) =

D Cr

^{r S r} ( ^{Х с ( r} ) ) ^1/3

g ( r) = k ( r) хС-г ( r).

Уравнения (18) и (19) следует решать совместно с законом сохранения числа частиц в системе:

/ \ 3

х™ = Xcr (t) + Zl-1 C (r, t).(11)

V a J

Одним из основных параметров разработанной модели является коэффициент диффузии атомов хрома в альфа-железе. Как следует из литературных данных [16] значение коэффициента диффузии сильно зависит от магнитного состояния сплава. При высоких температурах (выше температуры Кюри) сплав находится в парамагнитном состоянии, при низких температурах сплав переходит в ферромагнитное состояние, для которого коэффициент диффузии в значительной степени зависит от степени намагниченности сплава. В работе [16] экспериментально была определена зависимость коэффициента диффузии атомов хрома в сплаве Fe-Cr, находящегося в ферромагнитном состоянии:

D_Cr = 37.3 exp

267.4 kJ • mol ¹ [1 + ps ² ]

RT cm2/ s, (12)

где – параметр равный отношению намагниченности сплава при температурах T и 0, K, p = 0.133 . Для температуры 773K значение ps ² оказывается равным 0.091, что приводит к значению коэффициента диффузии при данной температуре равному 7.0 х 10^-19 cm ² / s .

Применение разработанной модели для описания кинетики зарождения и роста C - фазы в сплаве Fe-20at%Cr при температуре 773K приводит к удовлетворительному описанию экспериментальных данных [5] по зависимости концентрации кластеров (рис. 2) и их среднего радиуса (рис. 3) от времени отжига. При описании экспериментальных данных было определено соответствующее значение скорости зародышеобразования G = 1.0 х 10 ^{- 7} S ^{- 1} . Коэффициент диффузии считался равным представленному выше значе-

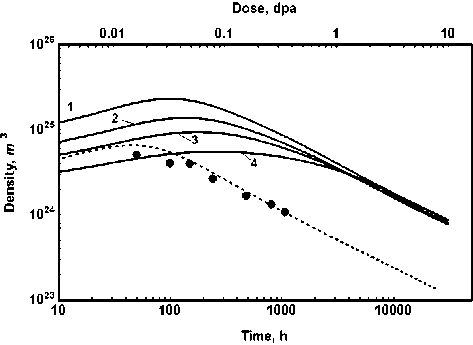
Рис. 2. Зависимость концентрации кластеров от времени отжига или продолжительности облучения (повреждающей дозы):

Точки – экспериментальные данные для Fe-20at%Cr при 773K [5]. Пунктирная линия результаты – расчета для Fe-20at%Cr при 773K. Сплошные линии -результаты моделирования для сплавов Fe-XCr под облучением: 1 – X = 20at%, 2 – X=16at%, 3 – X = 14at%, 4 – X = 12at%

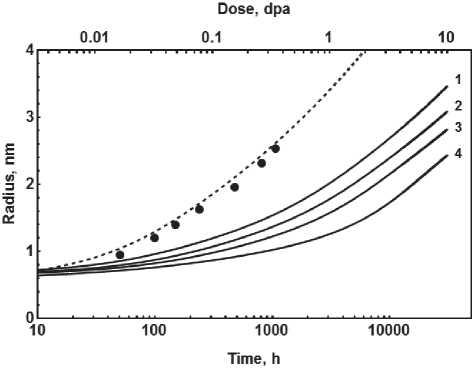
Рис. 3. Зависимость среднего радиуса кластеров

от времени отжига или продолжительности облучения (повреждающей дозы):

Точки – экспериментальные данные для Fe-20at%Cr при 773K [5]. Пунктирная линия результаты – расчета для Fe-20at%Cr при 773K. Сплошные линии -результаты моделирования для сплавов Fe-XCr под облучением: 1 – X = 20at%, 2 – X=16at%, 3 – X = 14at%, 4 – X = 12at% нию, вычисленному с помощью формулы (12).

Следует заметить, что соответствие экспериментальных данных и расчетных зависимостей при выбранном на основе экспериментальных данных коэффициенте диффузии является подтверждением корректности построенной модели. Кроме того, данное обстоятельство свидетельствует о возможности использования разработанной модели для определения коэффициента диффузии на основе анализа экспериментальных данных о росте частиц второй фазы [7].

Особенный интерес с точки зрения материа-

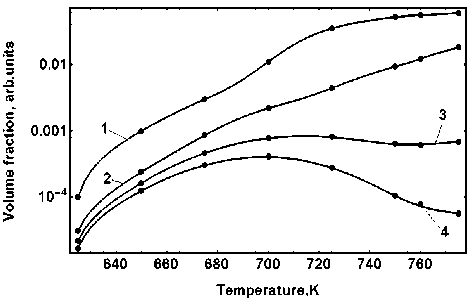
Рис. 4. Зависимость объемной доли - фазы в сплавах Fe-XCr от температуры отжига в течение 5000 часов:

1 - 20at.%Cr, 2 - 16at.%, 3 - 14at.%, 4 - 13 at.%;

точки – результат моделирования, сплошные линии – аппроксимация с помощью кубического сплайна ловедения представляет выявление условий соответствующих наиболее эффективному образованию частиц второй фазы. Поиск таких условий может быть проведен с помощью построения модельных кривых изохронного отжига для сплавов содержащих различные концентрации атомов хрома. На рис. 4 приведены результаты расчета зависимости объемной доли - фазы для нескольких сплавов на основе системы Fe-Cr в процессе термического отжига в течение 10000 часов. Как следует, из рисунка при снижении концентрации хрома область наиболее эффективного образования кластеров смещается в область более низких температур.

• 4.    МОДЕЛИРОВАНИЕ ПОВЕДЕНИЯ СПЛАВА Fe-Cr ПОД ДЕЙСТВИЕМ ОБЛУЧЕНИЯ

  • 4.1.    Радиационно-ускоренная диффузия в сплаве Fe-Cr

Одним из основных факторов приводящих к образованию кластеров под действием облучения является радиационно-ускоренная диффузия. Обычно предполагается, что радиационно-ускоренная диффузия обусловлена заметным (многократным) повышением концентрации вакансий под облучением, при этом коэффициент диффузии оказывается равным:

D cr C V*

D

*

Cr

e

V где CV, CV - концентрации вакансий в условиях облучения и термодинамического равновесия соответственно, DCr – коэффициент диффузии атомов хрома в железе в условиях термодинамического равновесия. Поскольку эксплуатация корпусных материалов атомных реакторов обычно проводится при температурах 573 — 623K , то соответствующий коэффициент диффузии атомов хрома следует определять с учетом ферромагнитного состояния сплава по формуле (12).

Расчет коэффициента диффузии при температуре 573K приводит к значению 2.2 х 10 ^{— 26} cm ² / 5 . Диффузия атомов хрома в железе в течение 10000 часов будет характеризоваться диффузионной длиной менее периода решетки, что позволяет сделать предположение об отсутствии обогащенных хромом кластеров в процессе термического отжига при данной температуре.

Проведем оценку радиационно-ускоренной диффузии атомов хрома в альфа-железе. Уравнения описывающие баланс поглощения радиационных дефектов стоками, а также процессов их генерации и рекомбинации может быть записано в виде:

G I

— kviCV CI — ki (CI — CI * )- 0

Gv — kviCv * Ci * — kv ( Cv * — CV *) - 0, (13)

где G_IV - скорость генерации вакансий и междоузлий в условиях облучения, k VI – скорость рекомбинации вакансий и междоузлий, k, V - мощность стоков, поглощающих вакансии и междоуз- e *

лия, Ci v - равновесное значение концентрации вакансий и междоузлий в условиях облучения. В качестве стоков радиационных дефектов чаще все- го выступают дислокации, поэтому мощность стоков обычно выражается через плотность дислокаций р , коэффициент диффузии соответствующего дефекта DIV, и поглощающей способности стока zA : kA - zADAp .

Результаты расчета радиационно-ускоренной диффузии атомов хрома проведенные с помощью формул (13) и параметров приведенных в табл. 1

при температуре 573K приведен на рис. 5. Представленные на рисунке значения коэффициента диффузии необходимо сравнить с соответствующим термическим значением полученным по формуле (13). Данное сравнение показывает, что коэффициент диффузии в условиях облучения оказывается почти на семь порядков больше, чем соответствующее термическое значение ( D_Cr - 2.2 х 10 ^{— 26} cm ² / 5 ).

Заметим, что коэффициент диффузии атомов хрома в условиях облучения оказывается величи-

DCr, 10-16cnn2/s

0.56 0.77   0.98     1-1       1.4       1.6

0.5         1.0         1.5

Dose rate, 10~7dpa/s

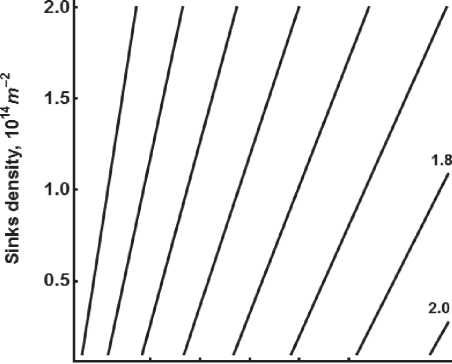
Рис. 5. Зависимость коэффициента диффузии атомов хрома в альфа-железе под облучением от плотности стоков и эффективной скорости смещений. Отложенные на сплошных линиях численные значения соответствуют коэффициенту диффузии при заданной скорости смещений и плотности стоков

Таблица 1. Параметры используемые для оценки радиационно-стимулированного коэффициента диффузии атомов хрома в железе при температуре 573K

Параметр

Зн ачени е

Коэффициент диффузии междоузлий [14], D- Коэффициент диффузии вакансий [14], Dv Равновесная концентрация вакансий [14], С-"- Скорость рекомбинации [14], у- Плотность дислокаций, Р Поглощающая способность междоузлий стоками, 3; Поглощающая способность вакансий стоками, !■■ Мощность стоков вакансий,-.'- . ку = ZyDyp Мощность стоков междоузлий, к ■ . ^ = ztDtp Каскадная эффективность, Скорость смещений, 6_

1.52 ■ 10"9 m2/s 1.85 ■ 10-16m2/s 7.62 ■ 10"14 9.31 ■ Ю11^1 1013 - 1014 m"2 1.2 1.0 0.371s"1 3.65 ■ lO^"1 0.25 10-8 — 10-7dpa/s

ной одного порядка с коэффициентом диффузии атомов хрома в процессе термического отжига при температуре 773 K. Так как данный термический отжиг сопровождается выделением альфа-штрих фазы, то можно ожидать, что облучение при температуре 573K также будет сопровождаться образованием обогащенных хромом кластеров.

Наряду с изменением коэффициента диффузии ввиду резкого увеличения концентрации радиационных дефектов можно было бы ожидать и некоторого изменения диаграммы фазового равновесия вследствие смещения химических потенциалов под действием облучения. К сожалению, приводимые в литературе экспериментальные данные о фазовом составе сплавов в условиях облучения не позволяют количественно оценить величину смещения фазового равновесия. В связи с этим, в дальнейшем будем полагать, что диаграмма фазового равновесия под облучением не изменяется.

• 4.2.    Моделирование кинетики образования кластеров в условиях облучения

С учетом сделанных предположений о характере радиационно-стимулированных процессов, разработанный выше подход может быть применен и для анализа образования кластеров в условиях облучения. Основную сложность применения разработанного подхода представляет отсутствие в литературе надежных кривых фазового равновесия при низких температурах 573-773K для исследуемого сплава Fe-Cr. Кривые фазового равновесия для сплава Fe-Cr, приводимые в различных работах (см. например [4, 17, 18]) могут заметно отличаются друг от друга. В данной работе были использованы результаты расчетов равновесной концентрации хрома в альфа-железе полученные [14]: X“_r = 7.7 at .% . Равновесный состав альфа-штрих фазы предполагался равным: X “ _r = 83 at .% .

Наиболее подробными экспериментальными данным по определению характеристик второй фазы альфа-штрих фазы под облучением являются результаты работы [6], полученные методом томографического атомного зондирования (TAP - tomographic atom probe). В данной работе после облучения сплава Fe-12at%Cr до повреждающей дозы 0.6dpa были обнаружены кластеры характеризуемые средним радиусом (1.1±0.2) nm, концентрацией (5.0 + 0.5) x 10 24 , m 3 , составом (58.5 + 1.1) at .% , концентрация атомов хрома в матрице при этом составила (8.24 + 0.05) at .% .

С помощью разработанной модели был проведен расчет кинетики выделения частиц второй фазы при температуре T = 573K , в условиях облучения. Скорость смещений атомов под облуче- нием принималась равной 0.9 x 10 7 dpa / 5. Расчет зависимости фазового состава от размера кластеров проводился с помощью уравнений (3), а зависимостей среднего радиуса кластеров, их концентрации и состава с помощью уравнений (8-11). Расчет проводился так, чтобы удовлетворить экспериментальным данным полученным в работе [6] для сплава Fe-12at%Cr. При этом варьировались коэффициент диффузии DC*r и скорость зарождения кластеров минимального размера G . Полученные при подборе значения оказались равными D*г = 1.4 x 10 9cm2/ 5 и g* = 5.4 x 10 85 '. Полученное значение коэффициента диффузии атомов хрома под облучением хорошо согласуется с расчетными данными для коэффициента диффузии полученных в п. 4.1.

На рис. 2 и 3 представлены результаты расчета среднего радиуса и концентрации кластеров в зависимости от дозы вплоть до 10 dpa для сплавов содержащих различные концентрации атомов хрома. Как следует из рисунков характер роста а' - фазы в условиях отжига при температуре 773 K и под действием облучения при температуре 573K являются сходными. Основным механизмом роста частиц второй фазы как в условиях отжига, так и облучения является коалесценция.

ВЫВОДЫ

Таким образом, в настоящей работе получены следующие основные результаты:

• 1.    Анализ образования -фазы в сплаве Fe-Cr в условиях термического отжига и облучения может быть проведен на основании разработанного в данной работе подхода и представлении о термическом и радиационно-ускоренном механизмах диффузии.

• 2.    Под действием реакторного облучения происходит существенное ускорение диффузионных процессов по сравнению с условиями термодинамического равновесия. Данное ускорение обусловлено повышенным значением концентрации радиационных дефектов в условиях облучения. При анализе генерационно-рекомбинационных процессов радиационных дефектов были получены оценки коэффициента диффузии в условиях облучения, при этом коэффициент диффузии оказался на семь порядков выше, чем соответствующее термическое значение.

• 3.    Разработана модель радиционно-ускорен-ного образования и роста кластеров в сплаве Fe-Cr в процессе облучения. Результаты расчета согласуются с экспериментальными данными других авторов для повреждающей дозы 0.6 dpa. При расчетах был получен коэффициент диффузии атомов хрома в условиях облучения, который оказался равным D Cr = 1.4 x 10 ¹⁹ cm ² / 5 . Дан-

• ное значение хорошо согласуются с оценкой коэффициента диффузии полученного в данной работе при анализе генерационно-рекомбинационных процессов радиационных дефектов в условиях облучения.

Как следует, из расчетов характер выделения частиц второй фазы при температуре 773 K и в условиях облучения при 573 K и скорости смещения 0.9 X 10 ^ 7 dpa / 5 оказывается сходным благодаря тому, что коэффициенты диффузии для этих условий оказываются величинами одного порядка.

Работа выполнена при поддержке грантов РФФИ №12-02-97033-р_Поволжье_а и ФЦП “Научные и научно-педагогические кадры инновационной России на 2009–2013 гг.”.