Моделирование образования новых материальных поверхностей в процессах когезионного разрушения композита с адгезионным слоем
Автор: Глаголев В.В., Маркин А.А., Фурсаев А.А.
Статья в выпуске: 2, 2017 года.
Бесплатный доступ
Рассматривается докритическое упругопластическое деформирование трехслойного композита и процесс разделения слоев, сопровождающийся разрушением адгезионного слоя. Путем осреднения компонент напряжений в адгезионном слое по его толщине задача сводится к системе двух вариационных условий равновесности относительно полей скоростей склеиваемых слоев. При решении упругопластической задачи докритического деформирования выделяется δ-область, в которой достигнут критерий разрушения. С помощью повторного решения задачи докритического деформирования с известным законом движения границы δ-области находится распределение нагрузки (узловых сил), действующей со стороны δ-области на тело. На следующем шаге рассматривается изменение напряженно-деформированного состояния (НДС) тела в процессе разрушения δ-области. Решается упругопластическая задача при простой разгрузке δ-поверхности тела и сохранении внешней нагрузки, соответствующей началу процесса разрушения. В процессе δ-разгрузки возможно образование новых пластических областей, частичная разгрузка и достижение критерия разрушения. В результате НДС тела в момент начала локальной разгрузки отличается от его состояния при окончании δ-разгрузки. Это является принципиальным отличием от известной процедуры «убийства элементов», когда жесткость элемента после достижения критерия разрушения полагается близкой к нулевой. При этом состояние тела вне удаленного элемента считается неизменным, и возможность появления зон разгрузок и догрузок после исключения элемента не учитывается. В случае линейной упругости решение задачи с удаленной областью при фиксированной внешней нагрузке совпадает с решением, получаемым в результате δ-разгрузки в силу единственности решения и принципа суперпозиции. Однако решение упругопластической задачи при простом нагружении тела с удаленной областью не будет совпадать с решением методом δ-разгрузки. В статье приведены решения задач расслоения композита, иллюстрирующие метод простой δ-разгрузки как в линейно-упругой, так и в упругопластической постановках.
Композит, подход нейбера - новожилова, характерный размер, процесс разрушения, простой процесс, упругопластическое деформирование, вариационное уравнение, метод конечных элементов
Короткий адрес: https://sciup.org/146211678
IDR: 146211678 | УДК: 539.375 | DOI: 10.15593/perm.mech/2017.2.03
Текст научной статьи Моделирование образования новых материальных поверхностей в процессах когезионного разрушения композита с адгезионным слоем
PNRPU MECHANICS BULLETIN
Моделирование образования новых материальных поверхностей предполагает описание двух стадий процесса нагружения тела: докритической и посткритической. Докри-тическая стадия может быть описана в рамках известных уравнений механики деформируемого твердого тела как без учета нелинейных эффектов, так и в нелинейной (упругопластической) постановке. При этом основная проблема состоит в формулировке критериев перехода к посткритической стадии. Общая постановка задачи посткритического поведения при упругопластическом деформировании далека от завершения. Это связано, во-первых, с выбором условий прекращения взаимодействия между поверхностями, во-вторых, с необходимостью формулировки граничных условий на вновь образуемых поверхностях. Если разрушение локализуется на материальной поверхности меры ноль, то имеет место классическая модель математического разреза [1-3]. Если взаимодействие прекращается в результате разрушения слоя конечной толщины между поверхностями, то применяется концепция физического разреза [4, 5]. Наиболее изученными и обоснованными в настоящее время являются модели докритического деформирования. Так как в этом случае не происходит образования новых материальных поверхностей, то любой подход, согласующийся с экспериментом по определению предельной нагрузки, может быть рассмотрен в качестве модели предразрушения. Соответствующие модели применяются как для оценки трещиностойкости конструкций из однородных тел, биметаллов [6], так и из композиционных материалов, где адгезионные слои рассматриваются как область предполагаемого разрушения [7, 8]. Выделим модели, в которых явно присутствует параметр структуры среды [5, 8–12]. При выполнении того или иного критерия разрушения наступает фаза образования новых материальных поверхностей. Принципиальным моментом данного этапа является дискретность приращения поверхностей разрыва [13–15] и локализация процесса разрушения. При моделировании разрушения в пределах материальной поверхности меры ноль используются когезионные элементы [16–19] конечно-элементного пакета [20] или контактные элементы системы [21]. В работах [22– 24] рассмотрен широко используемый билинейный закон распределения взаимодействия в когезионной зоне от раскрытия трещины с ниспадающим участком. Основным недостатком данного подхода является то, что когезионные элементы должны располагаться на траектории разрушения, которая зависит от новых материальных поверхностей. Кроме того, различные законы когезионного взаимодействия и материальные характеристики когезионных элементов существенно влияют на распределение напряжено-деформированного состояния [25] и требуют экспериментального подтверждения.
Сложность описания разрушения материального объема при использовании падающего участка диаграммы растяжения [26, 28] связана с построением определяющих соотношений неустойчивого по Друкеру деформирования и их подтверждением в экспериментах. Основным подходом при конечно-элементном моделировании процесса разрушения является процедура kill element, подробно описанная в [21]. В этом случае по достижении в конечном элементе критериальной характеристики разрушения выделяемый материальный объем исключается из рассмотрения путем умножения локальной матрицы жесткости элемента на число, близкое к нулю. Отметим, что данная процедура является корректной при упругом деформировании, когда нагрузка и разгрузка определяются одинаковыми модулями в определяющих соотношениях. В случае упругопластического деформирования тела с удаляемым таким образом элементом необходимо учитывать возможную разгрузку.
В данной работе предлагается рассматривать процесс разрушения δ-элемента как локальную разгрузку от напряжений, действующих на тело со стороны δ-элемента, при неизменной внешней нагрузке. Дискретизация задачи методом конечных элементов предполагает описание взаимодействия между частицами тела посредством узловых сил [29, 30]. Считаем, что при разрушении материального объема, взаимодействующего с несколькими конечными элементами, узловые силы взаимодействия будут разгружаться до нуля в рамках простого процесса при неизменной внешней нагрузке, достигнутой к моменту разрушения. Таким образом, неустойчивое по Друкеру деформирование исключается из рассмотрения. Отметим, что определение узловых сил взаимодействия с удаляемым материальным объемом во внутренних точках деформируемого тела является отдельной задачей. В статье предложена процедура повторного нагружения тела без разрушаемого объема, но с найденным по его границе полем перемещений для нахождения соответствующих узловых сил.
1. Постановка задачи
На рис. 1 представлено тело, состоящее из трех частей с различными материальными свойствами, где область 3 ассоциируется с клеевой подложкой толщиной δ 0 , размер которой мал по сравнению с толщинами тел 1 и 2 . Процесс нагружения предполагаем
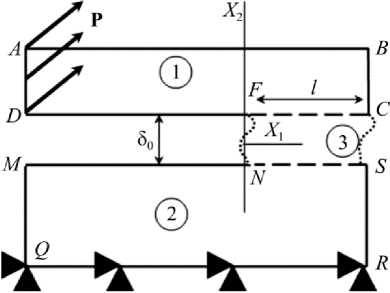
Рис. 1. Нагружение составного тела
Fig. 1. The loading of the compound body
квазистатическим и изотермическим. Условие равновесного протекания процесса [31] при малых деформациях и поворотах материальных волокон принимаем в виде
JJ о • •S w ds = J P • S v dl , (1)
SL где v - поле скоростей; w = 0,5 (Vv + vV) - тензор деформации скорости; V = ei —;
5 x i
5 P
P = — - скорость внешней нагрузки на 5 t
5о контуре L; о = — - скорость тензора напряжений;
5 t t – параметр подобный времени;
S = S 1 + S 2 + S 3 - внутренняя область составного тела.
В области 3 средние по толщине δ 0 скорости напряжений определяем в виде
12 1 2 12
СТ21 ( Х 1 ) = — f (^ 21 ( x i, x 2 ) dx 2 , СТ 12 ( x ) = — J 0 12 ( Х^ X 2 ) dx 2, О22 ( x ) = — J О22 ( Х^ X 2 ) dX 2,
δ 0 δ 0 δ 0 δ 0 δ 0 δ 0
CT11 ( X 1 ) = J CT11 ( X 1 , X 2 ) dX 2
80 -W
а средние скорости и скорости деформаций – через их гра- ничные значения:
w22
( X1 ) =
^ v + ( X 1 ) - v 2 ( X 1 )
< 80 >
w11
( x ) = 0,5
'o' / (x)
< 5 X 1
+ 5 v - ( X 1 ) ^ 5 x 1 v
S v C x ) = v , Ц ) - v , Ц ) 5 v 2 ( X 1 ) = 0 5 f 5 v + ( X 1 ) + 5 v 2 ( X 1 ) 5 x 2 80 5 X 1 ’ ^ 5 X 1 5 X 1 v
v 1 ( X 1 ) = 0,5 ( v 1 + ( X 1 ) + v - ( X 1 ) ) , v 2 ( X 1 ) = 0,5 ( v 2 + ( X 1 ) + v 2 - ( X 1 ) ) ,
где v + , v - - векторы скоростей верхней и нижней границы области 3 .
Из выражений (3) приходим к представлению средней скорости сдвиговой деформации вдоль рассматриваемой области:
w 21 ( X 1 ) = 0,5
<5 v 2 ( X1 ) + 5 v1 ( X1 )
v 5X1 5x 2
= 0,5
v +( X 1 )- v L( X 1 )
δ 0
+ 0,5
5 v 2 + ( X 1 ) 5 X 1
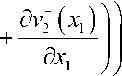
Принимаем, что векторы скоростей напряжений на сопряженных границах слоя 3 равны и противоположны векторам скоростей напряжений сопряженных границ тела. Кроме того, постулируется жесткое сцепление между границами области 3 и областями 1 , 2 :
v + = v ( X 1 ,80/2 ) ; v - = v ( X 1 , - 80/2 ) ; X 1 e [ F,C ] .
Рассматривая скорости граничных векторов напряжений слоя 3 в качестве граничных условий для смежных с ним областей [5, 8], приходим к совместному решению вариационных уравнений равновесия для тела 1 :
J о • -5 w ds + J о 22 5 v 2 dx 1 + J о 21 5 v 1 dx 1 + 0,55 0 J о 1
S1 t и тела 2:
I
5 dv , r^ 55 v2
—-1 dX i + о 21 ——
5 x ■ 5 x 1
dx^ = J P • 5 v dl (7)
J L 1
J о - -5 w ds - J о 22 5 v 2 dx 1 - J о 21 5 v 1 dx 1 + 0,55 0 J о 1
S 2
t
i
5 5 v , r^ 55 v2 ---1 dx + о21--- 2 5 x 1 21 5 x
dx 1 = J P -5 v dl . (8)
J L 2
Уравнения (7), (8) необходимо замкнуть конкретными определяющими соотношениями, связывающими скорости напряжений со скоростями деформаций. Поведение материала тел 1 и 2 при активном нагружении ( о --о > 0) определяем следующими физическими соотношениями:
о = 2 G ( i ) w , (9)
p = 3 K ( i )0 , (10)
где i = 1,2; о - скорость девиатора тензора напряжений; w - девиаторная составляющая тензора деформаций скоростей; p = о • ■ E ; K ( i ) - модуль объемного сжатия; G ( i ) - модуль сдвига G ( i ) = G ei ) при T < T ) , G ( i ) = G p ) при T > T pi ) ; T p ) - предел текучести соответствующего материала; T – интенсивность касательных напряжений.
В состоянии разгрузки (о ■ -is < 0) определяющие соотношения запишем в виде о = 2Geiyv ,(11)
p = 3 k ( i )0 .
В материале слоя определяющие соотношения считаем справедливыми для средних по толщине слоя скоростных характеристик НДС:
о = 2G (3)w, о --о > 0,(13)
о = 2Ge^^yv, о --о < 0, p = 3 K (3)0,(15)
где K ( 3 ) - модуль объемного сжатия материала слоя; G ( 3 ) - модуль сдвига материала слоя G ( 3 ) = G ef3 при T < T p3 , G ( 3 ) = G p 3^ при T > T p ) ; T ^3^ - предел текучести материала слоя.
В результате подстановки в определяющие соотношения (13)–(15) выражений компонент средних деформаций скорости (2), (5) средние скорости напряжений определяются через граничные скорости и их производные. Таким образом, решение системы (7)– (12) сводится к определению поля скоростей v ( x 1 , x 2 ) в телах 1 и 2 (см. рис. 1). В этом случае в уравнении (7) будут присутствовать скорости границы NS тела 2 (см. рис. 1), а в уравнении (8) – скорости границы FC тела 1 (см. рис. 1).
После определения поля скоростей для нахождения поля перемещений и деформаций используем эволюционные соотношения t1
u ( t 1 ) = J v dt , (16)
t 0
t 1
s ( t 1 ) = J w dt , (17)
t 0
где u ( x 1 , x 2 ) - поле перемещений; s - тензор деформации.
С учетом определяющих соотношений (9)–(12) находим поле напряжений в телах 1 и 2 :
t 1
о ( t 1 ) = J о dt , (18)
t 0
а из (13)–(15), используя значения граничных скоростей слоя и связи (2), (5), определяем поле средних напряжений слоя:
t 1
о ( t 1 ) = J о dt . (19)
t 0
Условия разрушения адгезионного слоя (АС) формулируем для δ-элементов слоя размером δ0×δ0. Это является следствием основного физического допущения – разрушение охватывает частицу материала с характерным размером δ0 [8, 11–15]. В качестве критерия когезионного разрушения АС будем использовать критерий Кулона, согласно которому разрушение δ-элемента происходит при достижении максимальным главным растягивающим усредненным напряжением критического значения: o max = о k , где
1 x 1 +5 0
6 j < 1 5 jA’ (20)
δ0 x1F а Gy получены в результате решения (7)-(12), (19).
2. Когезионное дискретное разрушение
Решение задачи докритического деформирования (7)–(15) строим на основе метода конечного элемента с квадратичным распределением поля скоростей на элементе. В этом случае поля скоростей напряжений и деформаций распределены по линейному закону в пределах каждого конечного элемента. Отметим, что размер грани конечного элемента может быть существенно меньше линейного размера 50 и определяется вычислительной сходимостью дискретного решения задачи [8]. Интегрируя по площади конечного эле- мента компоненты соответствующих тензоров, определяем средние по элементу значения
° у = - J о yd , ss
w ij
1 s
J w ij ds , s
по которым, используя эволюционные соотношения (17),
(18), находим напряжения и деформации оу, £у . Переход в состояние пластичности соотносим со средними характеристиками НДС. Решение упругопластической задачи строим на основе метода «упругих решений» [32]. Секущий модуль сдвига каждого конечного элемента будем определять исходя из средних компонент йд, Ед, считая секущий модуль в пределах конечного элемента постоянным.
Узел элемента характеризуется узловой скоростью vi и скоростью узловой силы F i . Используя эволюционные соотношения t1
U ( t i ) = J v i dt , (21)
t 0
t 1
F ( t 1 ) = J F i dt , (22)
t 0
в узлах можно определить узловые перемещения и узловые силы.
При когезионном разрушении постулируем, что элемент слоя полностью разрушается в течение интервала времени A t . В этом случае на момент разрушения t 1 мысленно удалим из слоя элемент размером δ0×δ0, где напряженное состояние, определяемое согласно (20), соответствует критериальной величине o max = о k , а его влияние на тело компенсируем внешней узловой нагрузкой F +( 1) , F -( j ) со стороны элемента (рис. 2).
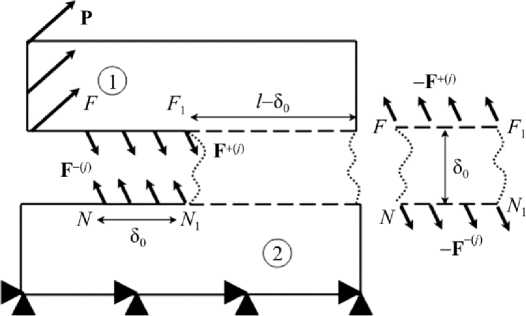
Рис. 2. Эквивалентные нагрузки элемента слоя в момент предразрушения
Fig. 2. The equivalent loadings of the element layer during the pre-fracture
Полагаем, что в течение интервала A t 5-элемент будет полностью разрушен, если нагрузка, действующая со стороны элемента слоя на тело, станет равна нулю. В этом случае в течение интервала времени A t при неизменной внешней нагрузке P необходимо разгрузить новые материальные поверхности. Будем считать процесс разгрузки простым, зависящим от одного параметра A t . Это соответствует заданию скоростей узловых внешних нагрузок:
F FF 1 = _ F +( i )/A t , F NN1 =- F -( j )/A t . (23)
Таким образом, рассматривая (23) в качестве внешней нагрузки, показанной на рис. 3, для конечно-элементной постановки задачи (7)–(15) можно смоделировать процесс формирования новых поверхностей на характерном размере. Процесс простой разгрузки на ин- тервале At может быть разбит на несколько интервалов, однако в рамках данной статьи ограничимся одним шагом.
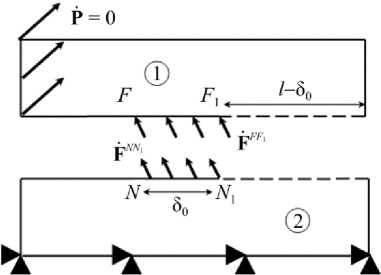
Рис. 3. Нагрузка в процессе разрушения элемента слоя
Fig. 3. The loading during the fracture of the layer element
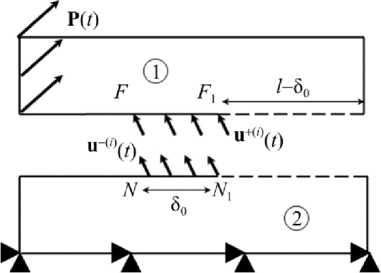
Рис. 4. Схема повторного нагружения
Fig. 4. The scheme of re-loading
Основная проблема заключается в нахождении узловых сил F +( 1 ) , F - ( j ) в момент предразрушения и, следовательно, в формировании граничных условий (23). Дискретное решение (7)–(15) для докритического деформирования по границам сопряжения слоя в качестве неизвестных содержит вектор узловых скоростей v +( 1 ) , v - ( j ) , по которому из (16) может быть сформирован вектор перемещений u +( 1 ) , u -( j ) .
Для определения узловых сил F +( 1 ) , F -( j ) предлагается использовать процедуру повторного нагружения, состоящую в замене действия разрушаемого элемента заданием процесса изменения со «временем» узловых перемещений элемента, при повторении закона внешнего воздействия на тело (рис. 4).
Конечно-элементное решение повторного нагружения в узлах с заданным полем узловых скоростей v +( 1 ) , v -( j ) в качестве неизвестных будет содержать вектор скоростей узловых сил F +( 1 ) , F -( j )
по границам разрушаемого элемента.
В зависимости от распределения основной внешней нагрузки в результате разрушения δ-элемента процесс разделения может продолжаться при неизменном значении основной внешней нагрузки (неустойчивое разрушение) либо прекратиться. При этом следует учитывать, что в результате δ-разгрузки, связанной с разрушением АС , в окружающих слоях может происходить догрузка с выходом в пластическую область. Данное обстоятельство не позволяет непосредственно использовать теорему о разгрузке А.А. Ильюшина [32].
3. Результаты решения
В качестве примера расчета рассмотрим композиционный материал в состоянии плоской деформации, состоящий из двух элементов с материальными характеристиками, близкими к сплаву Д16: G = 2,8 - 1010 Па; G p = 5,2 - 108 Па ; K = 6 - 1010 Па ; T p = 3 - 108 Па -предел упругости; о k = 4,2 - 108 Па - предел прочности, связанных эпоксидной смолой со следующими свойствами: G = 1,3 - 10 9 Па; K = 1,7 - 10 9 Па; о k = 9 - 10 7 Па. Геометрические характеристики композита выбирались следующими: AD = 5 - 10 - 3 м; 50 = FN = 10 - 3 м;
MQ = 2 - 10 2 м; AB = 10 - 1 м; DF = 5 - 10 - 2 м. Скорость внешней нагрузки P = 1 Па/с направлена по углом л/4 к оси 0 X 1 .
В качестве тестовой рассмотрим задачу разрушения элемента слоя в упругой постановке. Пусть критическое состояние в 6-элементе определяет внешняя нагрузка P = 1 Па. Вычислительная сходимость решения предполагает разбиение участка границы, сопряженного с δ-элементом, на четыре конечных элемента [8]. С учетом квадратичного закона распределения поля скоростей на конечном элементе девять узловых сил по верхней и нижней границе разрушаемого δ-элемента будут определять равновесие композита в момент предразрушения (см. рис. 2). Соответствующие значения узловых сил, определяемые методом повторного нагружения, представлены в таблице. Силы в таблице отнесены к минимальному значению модуля их проекций. Нумерация узлов выбрана слева направо.
Значения проекций безразмерных узловых сил
The values of the projections of the dimensionless nodal forces
|
* |
8,9 |
3,2 |
1,3 |
2,3 |
1,1 |
2,1 |
1,0 |
2,0 |
1,0 |
|
F 2 + |
–10,5 |
–9,8 |
–4,3 |
–8,3 |
3,9 |
–7,4 |
–3,5 |
–6,6 |
–3,3 |
|
F |
7,5 |
–2,2 |
–1,5 |
–3,0 |
–1,5 |
–2,9 |
–1,4 |
–2,8 |
–1,4 |
|
F 2 " |
–5,5 |
9,4 |
4,7 |
8,9 |
4,2 |
8,0 |
3,8 |
7,2 |
3,6 |
Без ограничения общности минимальный модуль проекций найденных узловых сил может быть рассмотрен в качестве параметра локальной разгрузки A t для определения граничных условий (23).
График 2 на рис. 5, а показывает распределение безразмерных вертикальных перемещений u 2 b по границе тела 1 и слоя 3 к концу докритического деформирования, график 3 – перемещений за счет процесса разрушения структурного элемента слоя, график 1 – суперпозицию полей перемещений. Перемещения отнесены к значению перемещения и + ( 0,60/2 ) на начало процесса разрушения. Безразмерная координата в направлении оси абсцисс определяется как x b = x 1 /6 0 .
График 1 на рис. 5, б определяет соответствующие вертикальные перемещения при решении задачи без первого структурного элемента слоя к концу интервала A t 1 . Данное решение моделирует подход kill element, используемый в процедурах конечноэлементного моделирования [15].
График 2 на рис. 5, б повторяет кривую 1 на рис. 5, а . Как видно из рис. 5, б , совпадение графиков 1 и 2 показывает адекватность предлагаемой процедуры разгрузки новых поверхностей в процессе разрушения и подхода kill element в рамках упругого деформирования. Отметим, что по горизонтальным перемещениям тенденция аналогична.
Максимальное главное растягивающее напряжение σ ˆ max во втором элементе слоя при этом возрастает, что предполагает катастрофический характер разрушения в данной схеме.
Проводя сравнение решения упругой задачи для заданной внешней нагрузки с первым структурным элементом слоя и без него, отметим, что для большинства конечных элементов интенсивность напряжений (I = о --о) уменьшается. На рис. 6 показана конечно-элементная область тел 1 и 2 (см. рис. 1), где интенсивность напряжений уменьшилась (элементы выделены заливкой) при решении задачи без первого структурного элемента слоя по сравнению с решением со структурным элементом. Данное обстоятельство дает право предположить, что при упругопластическом характере деформирования возможно образование зоны разгрузки пластических областей.
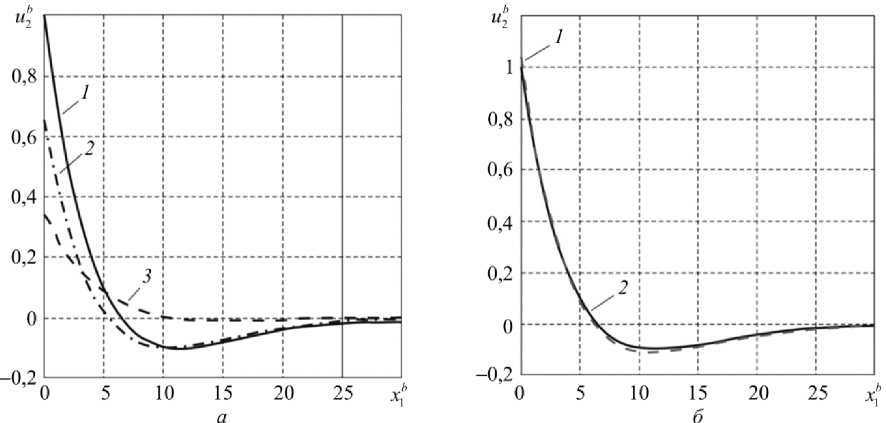
Рис. 5. Распределения вертикальных перемещений: а – штрихпунктирная линия – докритическое деформирование, пунктирная линия – процесс разрушения структурного элемента, сплошная линия – суперпозиция решений; б – сплошная линия повторяет соответствующую линию ( а ), пунктирная линия описывает докритическое деформирование без первого структурного элемента Fig. 5. The distribution of vertical displacements: a – the broken line shows the subcritical deformation; the dashed line shows the fracture of the structural element; the solid line shows the superposition of the solutions; б – the solid line repeats the corresponding line ( а ); the dashed line shows the subcritical deformation without the first structural element

Рис. 6. Конфигурация конечно-элементной области, где уменьшается интенсивность напряжений при упругом решении задачи, построенная на основе подхода kill element. Элементы выделены цветом
Fig. 6. The configuration of the finite element area where the stresses intensity decreases in the elastic solution of the problem based on the kill element approach. The elements are highlighted.
Однако подход на основе процедуры kill element не позволяет корректно описать данный процесс. Рассмотрим решение данной задачи на основе предлагаемой процедуры.
На рис. 7 выделена область пластических деформаций в состоянии предразрушения. Значение внешней нагрузки при этом обозначим через P k . Максимальное главное напряжение в адгезионном слое на характерном элементе равняется пределу прочности, а вне слоя предел прочности не достигается. Следовательно, разрушение в слое наступит быстрее, чем в сопряженных с ним материалах. Предполагаем, что адгезионная связь смола–сплав достаточно прочна и разрушение будет проходить по массиву адгезионного компонента.
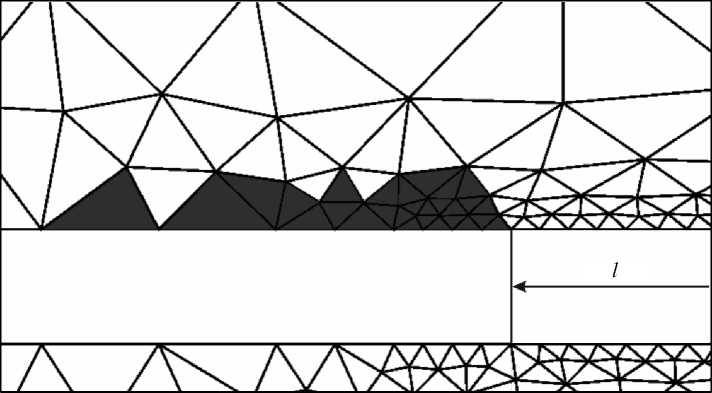
Рис. 7. Зона пластичности в состоянии предразрушения. Область выделена цветом Fig. 7. The plasticity zone in the pre-fracture state. The area is highlighted
Разрушение первого элемента приводит к перераспределению зоны пластичности и разгрузке ряда элементов композита. В этом случае рассмотрение разрушения как термомеханического процесса дает отличный от процедуры kill element результат. На рис. 8 темным показана зона пластической догрузки, а более светлым – элементы, где произошла упругая разгрузка из пластической области по завершении процесса разрушения первого δ-элемента.
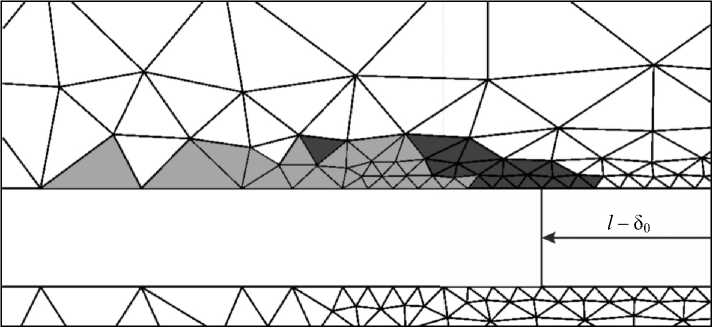
Рис. 8. Эволюция зоны пластичности и разгрузки в процессе разрушения первого элемента. Область разгрузки выделена серым цветом, а упругопластическая – черным
Fig. 8. The evolution of the plasticity and unloading zones during the fracture of the first element. The unloading area is highlighted in gray; the elastoplastic area is in black
Решая задачу нагружения композита критической нагрузкой P k без первого структурного элемента слоя, приходим к перераспределению пластической области (рис. 9). Сопоставляя рис.8 и рис. 9, видим, что разгрузка из пластической области не учитывается в подходе kill element, при этом область пластичности немного больше объединения областей разгрузки из пластической области и пластической догрузки, отображенных на рис. 8.
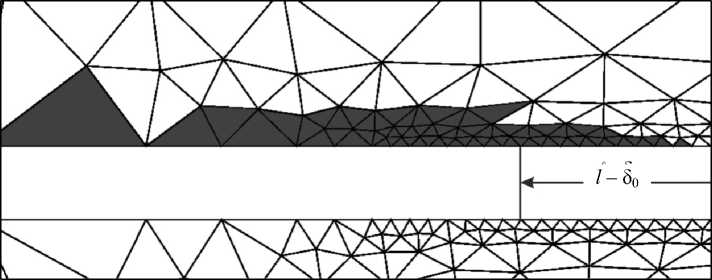
Рис. 9. Зона пластичности в композите без первого структурного элемента адгезионного слоя. Область выделена цветом
Fig. 9. Plasticity zone in the composite without the first structural element of the adhesive layer. The area is highlighted
Разрушение первого элемента приводит к превышению предела прочности на втором элементе слоя, что означает его разрушение при фиксированной внешней нагрузке. Таким образом, при данном виде нагружения имеет место катастрофическое разрушение.
Заключение
В работе предложен вариант описания дискретного разрушения материального объема на основе гипотезы простой разгрузки. Для определения внутренних узловых сил, действующих на разрушаемый объём, использована процедура повторного нагружения с заданным полем узловых перемещений, найденным из решения задачи докритического деформирования. Результаты расчёта по предложенной модели в рамках упругого поведения материала не противоречат известной методике расчета kill element. В случае упругопластического материала напряженное состояние, получаемое при моделировании процесса разрушения методом локальной разгрузки, может существенно отличаться от состояния, определенного методом kill element. Предлагаемый подход позволяет учесть перераспределение пластических зон и возможность образования новых зон разрушения в результате локальной разгрузки. Предложенная методика может быть использована для моделирования процесса разрушения элементов в произвольном конечно-элементном континууме .
Работа выполнена при финансовой поддержке РФФИ (грант № 15-01-01875).
Список литературы Моделирование образования новых материальных поверхностей в процессах когезионного разрушения композита с адгезионным слоем
- Черепанов Г.П. Механика хрупкого разрушения. -М.: Наука, 1974. -640 с.
- Партон В.З., Морозов Е.М. Механика упругопластического разрушения. -М.: Наука, 1985. -502 с.
- Barenblatt G.I. The Mathematical Theory of Equilibrium Cracks in Brittle Fracture//Advances in Applied Mechanics. -1962. -Vol. 7. -P. 55-129. -URL: http://dx.doi.o DOI: rg/10.1016/S0065-2156(08)70121-2
- Макклинток Ф. Пластические аспекты разрушения//Разрушение. -М.: Мир, 1975. -Т. 3. -С. 67-262.
- Glagolev V.V., Glagolev L.V., Markin A.A. Stress-Strain State of Elastoplastic Bodies with Crack//Acta Mechanica Solida Sinica. -2015. -Vol. 28. -No. 4. -P. 375-383 DOI: 10.1016/S0894-9166(15)30023-9
- Астапов Н.С., Корнев В.М., Кургузов В.Д. Модель расслоения разномодульного биматериала с трещиной//Физическая мезомеханика. -2016. -Т. 19, № 4. -С. 49-57.
- He X. A review of finite element analysis of adhesively bonded joints//Int. J. Adhes. Adhes. -2011. -Vol. 31. -No. 4. -P. 248-264 DOI: 10.1016/j.ijadhadh.2011.01.006
- Глаголев В.В., Маркин А.А., Фурсаев А.А. Моделирование процесса разделения композита с адгезионным слоем//Вестник Пермского национального исследовательского политехнического университета. Механика. -2016. -№ 2. -С. 34-44. 2016.2.03 DOI: 10.15593/perm.mech/
- Васильев В.В., Лурье С.А. Новое решение плоской задачи о равновесной трещине//Изв. РАН. МТТ. -2016. -Т. 51, № 5. -С. 61-67.
- Гольдштейн Р.В., Осипенко Н.М. Разрушение и формирование структуры//ДАН СССР -Т. 240, № 4. -1978. -С. 111-126.
- Нейбер Г. Концентрация напряжений. -М.; Л.: ОГИЗ: Гостехиздат, 1947. -204 с.
- Новожилов В.В. О необходимом и достаточном критерии хрупкой прочности//ПММ. -1969. -Т. 33, № 2. -С. 212-222.
- Назаров С.А., Паукшто М.В. Дискретные модели и осреднение в задачах теории упругости. -Л.: Изд-во Ленингр. ун-та, 1984. -93 с.
- Петров Ю.В. Квантовая аналогия в механике разрушения//Физика твердого тела. -1996. -Т. 38, № 11. -С. 3385-3393.
- Petrov Y.V., Morozov N.F., Smirnov V.I. Structural Macromechanics Approach in Dynamics of Fracture//Fatigue Fract. Engng. Mater. Struct. -2003. -Vol. 26. -No. 4. -P. 363-372 DOI: 10.1046/j.1460-2695.2003.00602.x
- Xiangting Su, Zhenjun Yang, Guohua Liu. Finite element modelling of complex 3D static and dynamic crack propagation by embedding cohesive elements in Abaqus//Acta Mechanica Solida Sinica. -2010. -Vol. 23. -No. 3. -P. 271-282 DOI: 10.1016/S0894-9166(10)60030-4
- Sua X.T, Yang Z.J., Liu G.H. Monte Carlo simulation of complex cohesive fracture in random heterogeneous quasi-brittle materials: A 3D study//International Journal of Solids and Structures. -2010. -Vol. 47. -No. 17. -P. 2336-2345 DOI: 10.1016/j.ijsolstr.2010.04.031
- Zhenjun Yang, X. Frank Xu. A heterogeneous cohesive model for quasi-brittle materials considering spatially varying random fracture properties//Computer Methods in Applied Mechanics and Engineering. -2008. -Vol. 197. -No. 45-48. -P. 4027-4039.
- Panettieri E, Fanteria D, Firrincieli A. Damage initialization techniques for nonsequential FE propagation analysis of delaminations in composite aerospace structures//Meccanica. -2015. -Vol. 50. -No. 10. -P. 2569-2585 DOI: 10.1007/s11012-015-0214-0
- Dassault Systemes Simulia Corp., Abaqus 6.11, User’s Manual, 2011.
- ANSYS. User's Guide, Release 11.0. -Pennsylvania, USA: ANSYS Inc., 2006.
- Dávila C.G., Camanho P.P., Turon A. Effective Simulation of delamination in aeronautical structures using shells and cohesive elements//Journal of Aircraft. -2008. -Vol. 42. -No. 2. -P. 663-672 DOI: 10.2514/1.32832
- De Moura MFSF., Gonçalves JPM. Cohesive zone model for high-cycle fatigue of adhesively bonded joints under mode I loading//International Journal of Solids and Structures. -2014. -No. 5. -P. 1123-1131. -URL: http://dx.doi.o DOI: rg/10.1016/j.ijsolstr.2013.12.0
- Finite element simulation of single carbon nanotube pull-outs from a cementitious nanocomposite material using an elastic-plastic-damage and cohesive surface models/Rashid K. Abu Al-Rub, Sun-Myung Kim, Khaldoon A. Bani-Hani, Nasser Al-Nuaimi, Ahmed Senouci//Int. J. Theoretical and Applied Multiscale Mechanics. -2014. -Vol. 3. -No. 1. -P. 31-57 DOI: 10.1504/IJTAMM.2014.069448
- Panettieri E., Fanteria D., Danzi F. Delaminations growth in compression after impact test simulations: Influence of cohesive elements parameters on numerical results//Composite Structures. -2016. -Vol. 137. -P. 140-147. -URL: http://dx.doi.o DOI: rg/10.1016/j.compstruct.2015.11.018
- Рыжак Е.И. К вопросу об осуществимости однородного закритического деформирования при испытаниях в жесткой трехосной машине//Изв. АН СССР. МТТ. -1991. -№ 1. -С. 111-127.
- Лебедев А.А., Чаусов Н.Г. Феноменологические основы оценки трещиностойкости материалов по параметрам спадающих участков диаграмм деформаций//Проблемы прочности. -1983. -№2. -С. 6-10.
- Стружанов В.В. Об одном подходе к изучению механизма зарождения трещин//ПМТФ. -1986. -№ 6. -С. 118-123.
- Kattan P.I., Voyiadjis G.Z. Damage Mechanics with Finite Elements: Practical Applications with Computer Tools. -Springer, 2012. -113 p.
- Efendiev Y., Hou T.Y. Multiscale Finite Element Methods. Theory and Applications. -Springer, 2009. -242 p.
- Маркин А.А., Соколова М.Ю. Термомеханика упругопластического деформирования. -М.: Физматлит, 2013. -320 с.
- Ильюшин А.А. Пластичность. Ч. 1. Упругопластические деформации. -М.: Изд-во МГУ, 2004. -376 с.


