Моделирование обтекания полупроницаемого тела на основе линейной кинематической модели методом крупных частиц

Full systematic results of investigation of flows around permeable bodies in all range of permeability are given in this article. Linear Davydov's kinematics condition is used for boundary formulation of surface of permeable body. Calculations are realized with Large-Particles Method. Bifurcation points of transition from one flow topology to another are finded.

Движение жидкости через пористую среду с различными параметрами проницаемости впервые рассмотрел НЕ. Жуковский [1,2]. Это направление затем было развито в трудах С.А. Христиановича [3-5], П.Я. Полубариновой-Кочиной [6-7], Х.А. Рахматулиным [8] и др. Для тонкого тела математическая модель проницаемости впервые была предложена в [8], где рассматривалась зависимость изменения нормальной составляющей скорости в виде многочлена от разности давления.

В данной статье излагаются результаты исследования обтекания полупроницаемого тела во всем диапазоне проницаемости: от полной непроницаемости (непротекания) до полной проницаемости. Эта задача решалась методом крупных частиц [9-11].

Ю.М. Давыдовым была предложена система кинематических и динамических моделей для обтекания полупроницаемого тела [12]. В данной статье используется линейная кинематическая модель Ю М. Давыдова. Граничные условия в рамках этой модели имеют следующий вид:

W,p=kWN, (1) где Wrp - значение вектора скорости на проницаемой границе, WN -нормальная к поверхности обтекаемого тела компонента вектора скорости потока у проницаемой преграды, к - линейный кинематический коэффициент проницаемости. Коэффициент проницаемости задавался в диапазоне 0 < k < 1, т е. от полного непротекания (к=0) до свободного невозмущённого течения через полностью проницаемую преграду (к=1).

Исследовалась задача обтекания тонкой пластины. Расчёты проводились на очень подробной разностной сетке 320x160. Сеточные параметры брались следующими: Ax=Ay=0,025, At = 0,0025. Высота полупроницаемой пластины R = 40Ау. Обтекаемая полупроницаемая пластина расположена на расстоянии 3R от левой границы расчетного поля. Рассматривались как плоский, так и осесимметричный случаи. В данной статье приводятся результаты для пространственно двумерного плоского случая при сверхзвуковом обтекании (М. = 2,0). Приводимые результаты соответствуют установлению течения при tk= nAt = 100 (n = 40000 - количество шагов но времени).

На серии рисунков (рис.1 - 14) показаны линии тока при обтекании полупроницаемой тонкой пластины. Отметим динамику изменения топологии течения в зависимости от коэффициента проницаемости. При к=0 на обтекаемом теле реализуются граничные условия пепротекания и течение имеет известную структуру с одной обширной кормовой зоной возвратно-циркуляционного течения (рис. 1) При очень малых значениях к > 0 топология сохраняется, при этом немного уменьшается протяженность зоны возвратно-циркуляционного течения и незначительно увеличивается расстояние между центром этой зоны и плоскостью симметрии (к-0,025), (рис. 2). При дальнейшем увеличении к структура течения резко изменяется: величина к=0,050 является бифуркационным значением коэффициента проницаемости. В задней окрестности верхней угловой точки обтекаемого тела образуются две дополнительных локальных зоны возвратно-циркуляционного течения (рис. 3). При дальнейшем увеличении к реализуются весьма сложные вихревые течения с рядом зон возвратно-циркуляционного течения. Величина к=0,075 соответствует рис. 4, к=0,100 - рис. 5, к=0,200 - рис. б, к=0,300 - рис. 7, к=0,400 - рис. 8, к-0,500 - рис. 9, к=0,600 - рис. 10, к=0,700 - рис. 11, к=0,800 - рис 12, к=0,825 - рис. 13, к=0,900 - рис. 14. В диапазоне к-0,050...0,800 за телом существуют протяженные зоны возвратно-циркуляционных течений. Величина К=0,825 является еще одним бифуркационным значением коэффициента проницаемости: происходит качественная перестройка и изменение топологии течения (см. рис. 13). Обширные зоны возвратноциркуляционного течения пропадают, сохраняется лишь небольшая область с замкнутыми линиями тока около кормы в окрестности плоскости симметрии. При к=1 во всей области течения мы наблюдаем невозмущенный плоско-параллельный поток.

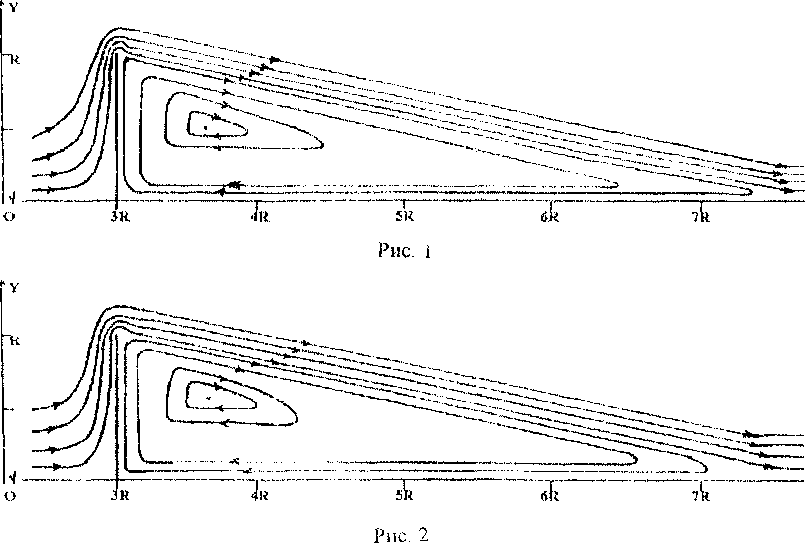
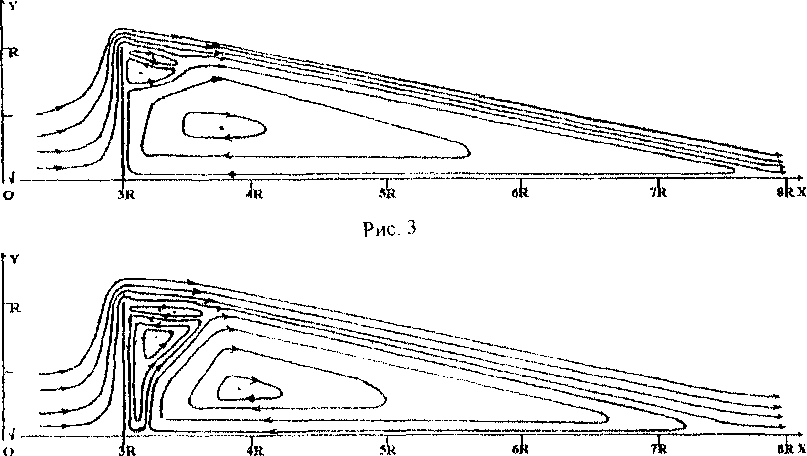
Рис. 4

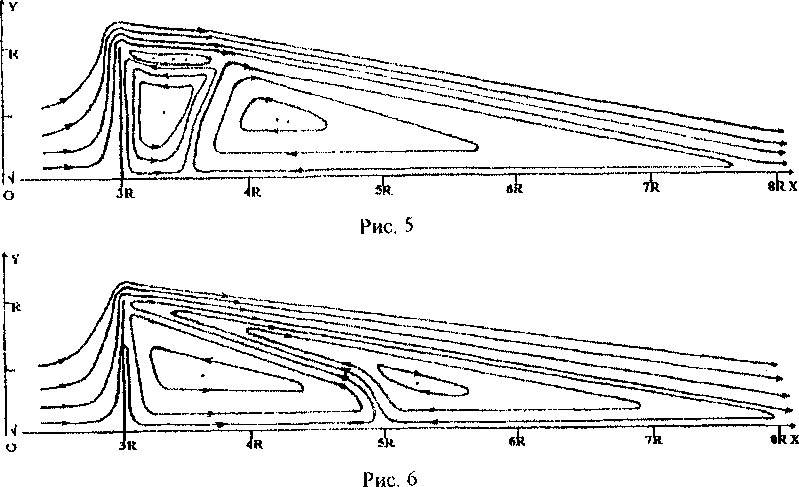
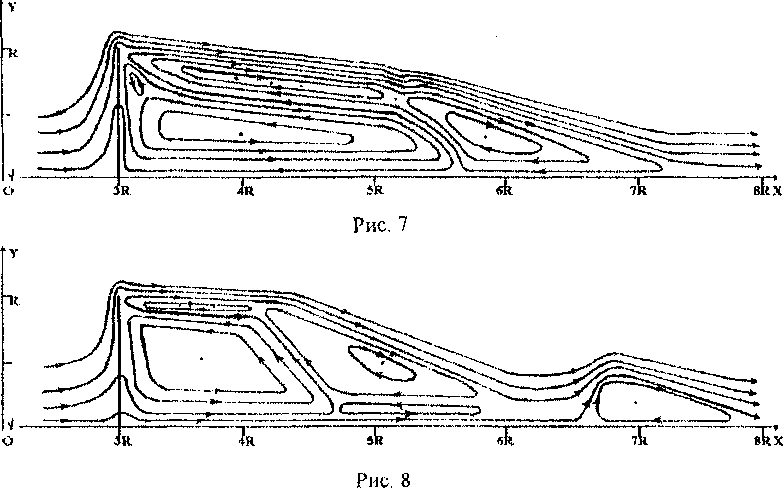
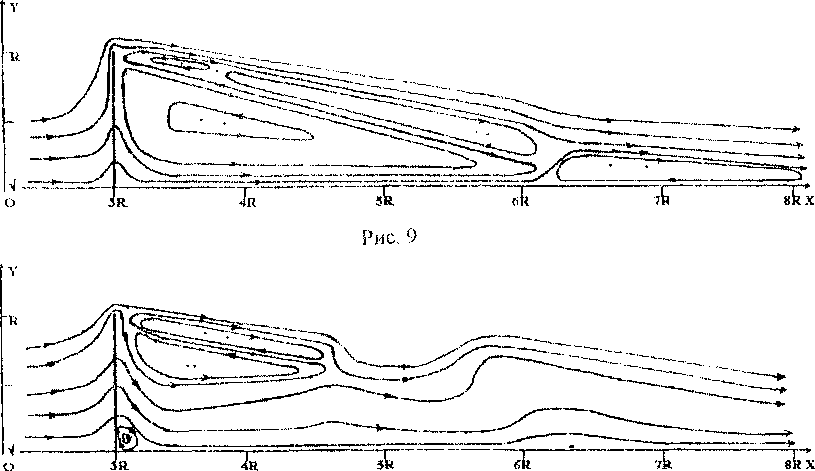
Рис. 10

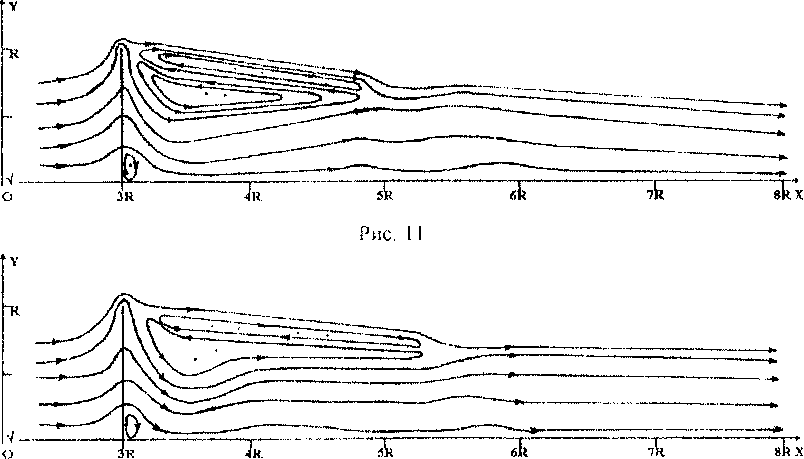
Рис. 12

Рис. 13

Рис. 14