Моделирование одномерного гармонического осциллятора в среде matlab/simulink

Жизненный цикл многих технических систем постоянно сопровождают различные колебательные процессы, оказывая на них либо вредное воздействие, либо, наоборот, позволяя эффективно исполнять предписанные им функции. Своими катастрофическими последствиями известны явления флаттера , шимми и бафтинга – интенсивных, часто внезапных, колебаний элементов конструкции самолёта. Другую аварийную ситуацию создаёт помпаж - вредные колебания в работе лопастных компрессоров, вентиляторов и насосов, как правило, приводящие к их разрушению.

Однако полезное техническое применение колебательных процессов гораздо разнообразнее. В частности, в машиностроении широко применяется ультразвуковая обработка материалов. Различные вибрационные машины используют для изготовления литейных форм, бурения горных пород, уплотнения дорожных покрытий, формования железобетонных изделий и погружения свай в грунт.

Для направленного перемещения сыпучих материалов, паст и жидкостей созданы вибрационные конвейеры, насосы, питатели, дозаторы и бункеры. Работа регуляторов и систем автоматического управления постоянно сопровождается колебательными процессами. Широкая гамма пьезорезонаторов нашла применение в газовом анализе.

Во всех видах морских флотов широко применяются гидроакустические приборы. Вся радиотехника и электроника основана на создании и преобразовании необходимых электромагнитных колебаний. На стыке акустики твердого тела, физики полупроводников и радиоэлектроники развивается акустическая электроника. При этом всё многообразие физико-технических систем, совершающих колебания, объединяется в класс осцилляторов , среди которых заметное место занимают гармонические одномерные осцилляторы, в том числе различные колебательные контуры и кварцевые резонаторы. Широкое распространение и перспективы технического применения подобных осцилляторов побуждают обратиться к их моделированию с использованием современных программных средств, в частности,        инструментального        пакета

MATLAB/SIMULINK, технология применения которого рассмотрена в этой статье.

Теоретические основы моделирования. В качестве теоретической основы построения искомой модели принято уравнение движения гармонического осциллятора, совершающего вынужденные одномерные колебания в условиях трения. Такое уравнение имеет вид [1]:

f x + 2Xx + <У0 x = — cos yt,             (1)

m где x – отклонение координаты осциллятора от её равновесного значения; X - коэффициент затухания колебаний; ω0 = ^k/ m - частота свободных или собственных колебаний осциллятора; m и k – вещественные константы, характеризующие физические свойства осциллятора и непосредственно определяющие параметры его свободных колебаний; f – амплитуда и γ – частота колебаний внешней возмущающей силы F(t).

совершаемых осциллятором под действием некой внешней силы F(t)=f ⋅ cos γ t , а при λ ≠ 0 и f =   0 преобразуется в уравнение

m ( ω ₀ ² - γ ² ) ² + 4 λ ² γ ² ,

2λγ tgδ=         .                         (4)

γ ² - ω ₀ ²

Приравнивая в разных сочетаниях вместе и по отдельности λ и f к нулю, из соотношения (2) можно получить различные решения уравнения (1), в том числе для свободных, вынужденных и затухающих колебаний осцилля- тора.

Уравнение (1) исчерпывающе описывает всевозможные движения широко распространённого в технике одномерного гармонического осциллятора, а уравнение (2) даёт его решение. Вместе соотношения (1) и (2) составляют совокупность готовых математических моделей поведения осциллятора в различных условиях, которые, однако, для практического применения требуют программной реализации, в частности средствами MATLAB.

Моделирование движения осциллятора средствами MATLAB. Располагая уравнением (1), заданную модель удобно получить, используя блок Integrator раздела Continuous библиотеки SIMULINK. Для этого соотношение (1) целесообразно переписать в виде

f

& x & = cos γ t - 2 λ x & - ω ₀ ² x .

m

Тогда порядок следования слагаемых правой части уравнении (5) сразу же даёт структуру искомой модели (рис. 1), которая самым естественным образом воспроизводит этот порядок.

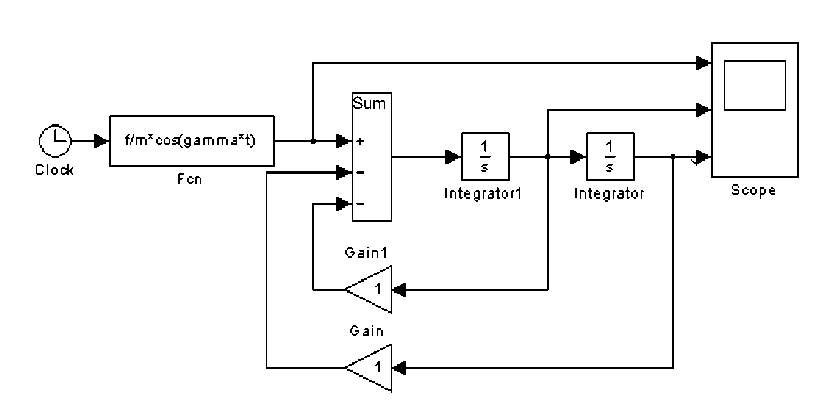
Рис. 1. Модель осциллятора на основе блока Integrator

Так, внешняя возмущающая сила задаётся блоком Fnc, первая производная, она же скорость осциллятора вычисляется блоком In-tegrator1, а перемещения осциллятора вычисляет блок Integrator. Блоки Gain1 и Gain предназначены для задания коэффициентов 2 X и О 0 . При этом все компоненты правой части (5) алгебраически суммируются блоком Sum, а графики изменения внешней силы, скорости и величины перемещения осциллятора выводятся в отдельные окна на один экран виртуального осциллографа Scope.

Для проведения вычислительного эксперимента построенную модель надлежит настроить, задав значения параметров осциллятора, начальные условия его движения и закон изменения внешней возмущающей силы. В условиях абстрактного эксперимента ничто не мешает положить массу осциллятора m = 5 кг, а свойственный ему коэффициент, например, упругости, k = 2 кг/с ² . Тогда квадрат частоты собственных колебаний такого осциллятора Ю 0 = k/m = 0,4 с ^-2 . Пусть также коэффициент затухания колебаний X =1,4 с ^-1 , а возмущающая сила F(t) действует на осциллятор с амплитудой f = 4 кг - м - с ^-2 и частотой у = 0,8 с ^-1 . В качестве начального условия движения осциллятора принято отклонение осциллятора от положения равновесия x = 0,05 м и x = 0.

Полученные в этих условиях результаты показаны на рис. 2.

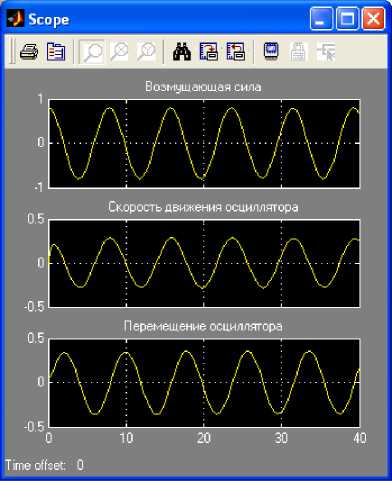
Рис. 2. Результат работы модели на основе блока Integrator при заданных условиях эксперимента

Аналогичную модель в среде MATLAB/SIMULINK можно построить несколько иначе, применив к исходному уравнению (1) преобразование Лапласа, которое при нулевых начальных условиях приводит его к виду s2 X(s) + 2XsX(s) + о>0X(s) = — F(s).

m

Тогда отношение

X ( s ) =     1/ m

F ( s ) s ² + 2 X s + 0

есть не что иное, как передаточная функция осциллятора. Такой подход позволяет применить для построения требуемой модели блок передаточной функции Transfer Fcn раздела Continuous библиотеки SIMULINK. Полученная при этом модель показана на рис. 3, а результаты её работы – на рис. 4.

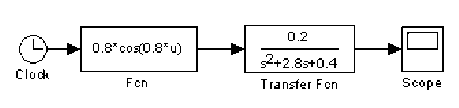
Рис. 3. Модель осциллятора на основе блока Transfer Fcn

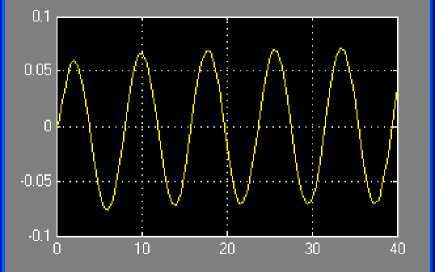
Рис. 4. результат работы модели на основе блока Transfer Fcn

На основании уравнения (2) получена модель (рис. 5), которая позволяет на одном экране виртуального осциллографа Scope получить сразу четыре графика колебаний осциллятора – вынужденных в условиях трения, свободных, затухающих и вынужденных без трения (рис. 6). Для этого в модели рис. 5 использованы четыре блока Fnc, настройки которых хорошо видны в пределах каждого блока.

Уравнение (2) даёт возможность получить искомые модели, используя MATLAB в режиме научного калькулятора. Для этого для прежних условий эксперимента в его команд-      операторов, результат выполнения которых ном окне набрана следующая совокупность показан на рис. 7:

• > > syms t;

• > > subplot(4,1,1); ezplot('0.05*exp(-1.4*t)*cos(0.63*t+1)+0.36*cos(0.8*t+1.36)',0,40);

• > > axis([0 40 -0.5 0.5]);grid;

• > > subplot(4,1,2); ezplot('0.05*cos(0.63*t+1)',0,40);axis([0 40 -0.05 0.05]);grid on;

• > > subplot(4,1,3); ezplot('0.05*exp(-1.4*t)*cos(0.63*t+1)',0,10);axis([0 10 -0.05 0.05]);grid on;

• > > subplot(4,1,4); ezplot('0.05*cos(0.63*t+1)+0.36*cos(0.8*t+1.36)',0,40);axis([0 40 -0.5 0.5]);grid;

  

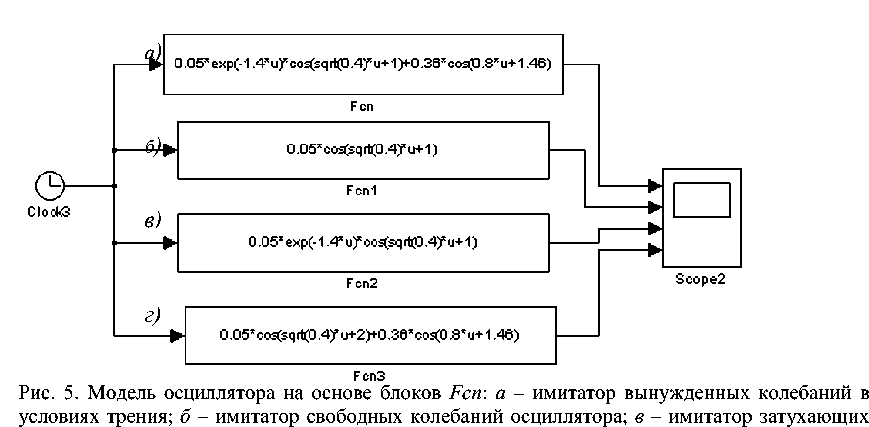
  колебаний; г – имитатор вынужденных колебаний без трения

  
  

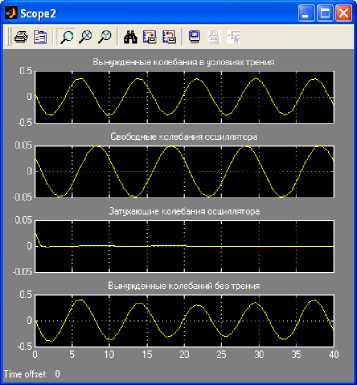
Рис. 6. Результат работы модели на основе блоков Fcn

Разработанный комплекс инвариантных моделей позволяет исследовать поведение многих распространённых в технике гармонических одномерных осцилляторов. Модели обеспечивают получение результатов экспериментов, взаимно дополняющих и подтверждающих друг друга. Результаты моделирования могут быть представлены в графической и табличной форме, а обладание передаточной

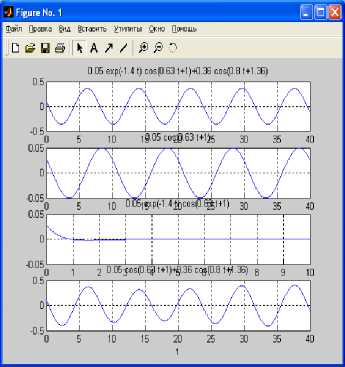
Рис. 7. Модели движения осциллятора, полученные при использовании MATLAB в режиме научного калькулятора функцией осциллятора позволяет развить его исследования в области устойчивости и частотных характеристик с построением диаграмм Николса, Найквиста и Боде.