Моделирование однонаправленного излучения микродисковых резонаторов с отверстиями методом Галеркина с точно вычисляемыми матричными элементами

В видимом и инфракрасном диапазонах света диэлектрические микроразмерные рассеиватели являются примерами конфигураций, демонстрирующих как геометрическо-оптические (лучеподобные), так и модовые эффекты. Наиболее известными из них являются линзы различной формы. В частности, круглый цилиндрический стержень и сферическая диэлектрическая частица концентрируют поле падающей плоской волны в узкое вытянутое фокусное пятно на теневой стороне, обычно называемое фотонной струей (PJ) [1 , 2] . Как и любой фокусирующий эффект, PJ является широкополосным (т.е. не резонансным) и имеет геометрически-оптическое происхождение [3] . Более того, если частота или радиус сферы или стержня увеличивается, то область PJ становится меньше, в то время как максимальная амплитуда поля в этой области линейно увеличивается. Однако помимо эффекта PJ, в ограниченных диэлектрических структурах обычно хорошо заметны резонансы на собственных модах. В частности, известно, что круглые диэлектрические стержни и сферы поддерживают моды шепчущей галереи (WG), которые имеют сверхвысокие Q-факторы, растущие экспоненциально с азимутальным индексом моды и радиусом. Когда мода WG возбуждается плоской волной, на диаграмме поля в ближней зоне наблюдаются азимутально периодические горячие точки вдоль обода полости, помимо фокальной области PJ. Поэтому моды WG портят фокусировку на дискретных частотах.

Согласно теореме взаимности электромагнитной теории, если поместить точечный источник в точке максимальной амплитуды поля PJ, то можно наблюдать «обратный эффект PJ». Это означает, что в направлении, противоположном направлению распространения плоской волны в рассеивающей конфигурации, возникает интенсивный лепесток излучения [4 , 5] . Этот «обратный» эффект также является широкополосным, и упомянутый интенсивный лепесток излучения заостряется, если оптический размер рассеивателя становится больше. Однако на дискретных частотах этот эффект коллимации пучка портится из-за возбуждения WG мод. Это происходит потому, что на диаграмме поля в дальней зоне вспыхивает множество одинаково интенсивных лепестков.

Как известно, PJ появляется вне круглого рассеивателя, если показатель преломления ν меньше 2. В противоположном случае, когда ν достаточно велик, фокальная область смещается внутрь рассеивателя

[1 –3] . Это наблюдение наводит на мысль, что размещение небольших рассеивателей в максимуме поля фокальной области микродискового лазера с высоким показателем преломления может быть использовано для усиления направленности излучения WG мод.

Тонкие круглые микродисковые лазеры, установленные на пьедестале или лежащие на низкоиндексной подложке, известны как микроразмерные источники благодаря сверхнизким порогам их мод WG [6] . Обычно они изготавливаются из высокоиндексных материалов, таких как GaAs (v = 3.4). Однако направленность их излучения низка из-за большого количества (в два раза больше азимутального индекса моды) одинаковых лепестков на диаграмме поля в дальней зоне. Этот недостаток круглых микродисковых лазеров послужил толчком к поиску лучшей формы. Среди наиболее перспективных форм были рассмотрены лимакон, змейка и спиралевидная форма [7 –9] . К настоящему времени сложился консенсус, что отклонения от круглой формы не должны быть существенными, чтобы не испортить высокие Q-факторы WG мод. В этом смысле резкая ступенька на ободе спиральной полости убивает Q-фактор, что перевешивает улучшение направленности. Тем не менее, следует подчеркнуть, что почти все публикации (за исключением случая формы змейки [8] ), посвященные поиску оптимальной формы, были основаны на анализе мод в пассивном резонаторе, где наличие активной области игнорировалось.

В данной работе нас интересует управление характеристиками WG мод с помощью небольшого круглого отверстия. Мы ожидаем, что отверстие может улучшить направленность WG мод и сохранить низкими пороги генерации, как это было впервые предложено в [10]. Нашим надежным вычислительным инструментом является набор граничных интегральных уравнений Мюллера (BIE) в двумерной модели микрополостного лазера, геометрия которого представлена на рисунке 1. Он рассматривается в рамках Lasing Eigenvalue Problem (LEP), предложенной для диэлектрических полостей с активным материалом без [11] и с элементами потерь [12]. В рамках LEP собственные значения модифицируются: каждое из них представляет собой пару вещественных чисел, частоту и порог генерации излучения. Используя метод дискретизации Галеркина с тригонометрическим базисом для BIE Мюллера [13] и учитывая наличие линии симметрии [14], мы получаем алгебраическую задачу на собственные значения. Сходимость этого численного метода относительно числа усечения матрицы полностью обоснована математически, см. работу [15], детали алгоритма представлены в [16, 17].

Предварительные результаты, существенно более полно раскрытые в данной статье, были доложены на научной конференции и опубликованы в ее материалах [18] .

• 1. Задача о собственных модах микрорезонатора с отверстием

Следуя [8] , сформулируем задачу о собственных модах двумерного диэлектрического микрорезонатора круглой формы с отверстием. Пусть показатель преломления в области Ω 1 (см. рисунок 1) , ограниченной контуром Γ 1 , известен и положителен, обозначим его ν o > 0. Пусть область резонатора Ω ₂ является активной областью, ограниченной контурами Γ 1 и Γ 2 . Показатель преломления в активной области равен v i = a i — iY, где a i > 0, y > 0 — порог генерации лазерного излучения. Пока затель преломления во внешней неограниченной области Q 3 = R 2 \ Q 1 U Q 2 , равен показателю преломления окружающей среды ν o > 0.

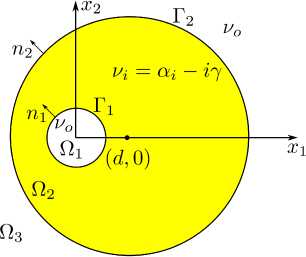
Рисунок 1. Геометрия двумерного диэлектрического микрорезонатора круглой формы с отверстием

Мы предполагаем, что границы Γ ₁ и Γ ₂ являются дважды непрерывно дифференцируемыми замкнутыми кривыми, не касающимися друг друга. Обозначим единичный вектор внешней нормали к границе Γ _i буквой n _i , i = 1, 2. Обозначим символом U пр ост ра нство всех комплекснозначных функций, непрерывных в Ω 1 , Ω 2 и Ω 3 , и дважды непрерывно дифференцируемых в открытых областях Ω 1 , Ω 2 и Ω 3 .

Пусть значение параметра y > 0 зафиксировано. Ненулевую функцию u ∈ U будем называть собственной функцией задачи, соответствующей собственному значению к >  0, если выполняются следующие соотношения: уравнения Гельмгольца,

• (1)                     Au + к2и = 0,  x е

• (2)                     Au + k2u = 0,  x е

• (3)                     Au + k2u = 0,  x еU

  условия сопряжения,
  (4)	и = и + ,	∂u -     ∂u +	, x е Г 1
  		П о 1Щ = n i дЩ
  (5)	и - = и + ,	∂u -     ∂u +	, x е г 2
  		n i я— = П о я— ∂n 2      ∂n 2
  и условие излучения Зоммерфельда,
  (6)	( - ∂ρ	ik o ^ и = o( - 1Р ),	ρ → ∞ .

Здесь k j = kv j — волновое число в соответствующей области, n j = v -² в случае H -поляризации, и n j = 1 в случае E-поляризации, j = i, o ; и ^- (и ⁺ ) — предельные значения функции и изнутри (извне) контура r i , i = 1,2.

Следуя [19] , с. 68, мы предполагаем, что предельные значения (правильной) нормальной производной

∂u ^±

• (7)    ——( x) = lim (n i (x), grad u(x ± hn(x))), x е r i , i = 1, 2, ∂n _i      h →+0

существуют равномерно по x на r i , i = 1,2.

Будем разыскивать нетривиальные решения задачи (1) — (6) в пространстве комплекснозначных функцийй U. При фиксированном значении параметра y > 0, ненулевую функцию и, удовлетворяющую условию излучения Зоммерфельда, будем называть собственной функцией задачи о собственных модах двумерного диэлектрического микрорезонатора круглой формы с отверстием, отвечающей собственному значению к > 0, если выполнены условия (1) — (5) .

ному значению k то, как доказано в [16] , справедливы следующие интегральные представления:

• (8)    u = - / ( ^dG ° ^(k; xy) u ^- (y) - J гЛ dn i (y)

  - G o ⁽k; x,y) ^du ^(y) ) dl⁽y⁾, x G « i , dn i (y)

• (9)    u = [ ⁽ ' u +_W - G ₁ (k,Y;x,y) du+M W) - J гР   dn i (y)                         dn i (y)

  
  

[ ( ^^Y ^;Х^,У) u - (y) — G i (k,Yxx,)du - y) ) d(y), x G « 2 , J r2^V    dn 2 (y)                         dn 2 (yp

• (10)    u = / ( ^{dG o (k};^x,y) u + (y) - G o (kxryy) ^du ⁺ y))dl^, x G « 3 , г ₂\ dn 2 (y)                         dn 2 (y)

где G j (x,y) = (i/4)H 0¹⁾ (k j | x — y | ), j = i, o , H0^{1 1} — функция Ханкеля первого рода нулевого порядка.

Используя условия сопряжения (4) и (5) , определим функции

(11)	U j = u + = u , x G Fj- ,   j = 1, 2,
(12)	= n i + П о du + = П г + П о du -       r Xi       2n o dn i        2n i dn i ,           i ,
(13)	= П г + П о du + = П г + П о du —       „ x2       2П г dn 2       2П о dn 2 , Х Е 2.

Сложим почленно предельные значения интегральных представлений

(8) — (10) и их нормальных производных с обеих сторон от контуров

Г1, Г2, используя при этом хорошо известные свойства потенциалов простого и двойного слоя (см., напр., [19], с. 47), получим однородную систему граничных интегральных уравнений Мюллера относительно функций u и v :

• ⁽¹⁴⁾    u i ^(x)+[ ^u i ⁽y^{)K 1},^{1 (x,}y^)dl(y⁾+ [ ^v i ⁽y^{)K 1},^{2 (x,}y^)dl(y⁾+ Γ 1                                   Γ 1

+ [ u 2 ⁽y^)Ki ^{3 (x,}y^)dl(y⁾+ [ ^v 2 ⁽y^)Ki 4 ^(x,y^)dl(y⁾ = ⁰, ^{x G r} i Γ 2                                 Γ 2

• (15)    vi(x)+ [ u1(y)K2’1(x,y)dl(y)+ [ v1(y)K2’2(x,y)dl(y)+ Γ1

+ [ u2(y)K2,3(x,y)dl(y)+[ v2(y)K2,4(x,y)dl(y) = 0, x e ri, Γ2

• (16)    u2(x)+[ ui(y)K3’1(x,y)dl(y)+ [ vi(y)K3’2(x,y)dl(y)+ Γ1

+ [ u2(y)K23(x,y)dl(y) + [ v2(y)K2 4(x,y)dl(y) = 0, x e r2, Γ2

• (17)    v2(x)+ [ u1(y)K4,1(x,y)dl(y)+ [ vi(y)K4’2(x,y)dl(y) + Γ1

3. Метод Галеркина

x e Г 2 ,

⁺ [ ^u 2 ⁽y^{)K 4}’3 ^(x,y^)dl(y⁾⁺ [ v 2 ⁽y^{)K 4 , 4 (x,}y^)dl(y⁾ = ^0, Γ 2                                 Γ 2

где ядра интегральных уравнений имеют вид

(18)	K 1’1 =	dG o (x,y)   dG i (x,y)         _	Г 1 ,
		dm(y)      dm(y) , x e 1 ,y e
(19)	K ^’2 =	^П^ G i (x,y) -      G o (x,y), x П г + П о            П г + П о	e r 1 ,y e r 1 ,
(20)	k 1 ’ 3 =	dG 4 (x,y) д      X , x e 11/У e r 2 , dn 2 (y)
(21)	k 1 4 =	2n o G i (x,y) , x e Г 1 , y e Г 2 , П о + n
(22)	K 21 =	d 2 G o (x,y)       d 2 G i (x,y)	Г 1 ,у e Г 1 ,
		dn 1 (x)dn 1 (y) dn 1 (x)dn 1 (y) ’
(23)	k 2 ’ 2 =	2n o dG i (x,y)     2п г dG o (x,y)	x e Г 1 ,у e Г 1
		П о + П г dn 1 (x)      H o + П г dn 1 (x) ,
(24)	k 2 ’ 3 =	д 2 G i (x,y)
		Л                \ , x e Г 1 , y e Г 2 , дп 1 (х)дп 2 (у)
(25)	k 2 ’ 4 =	2n o dG i (x,y)
		.        r-j / х , x e Г 1 , y e Г 2, n o + П г дП 1 (х)
(26)	K 2’1 =	dG i (x,y) Д      x , x e Г 2 , y e Г 1 , dn 1 (y)

120	И.В.	Кетов, А. О. Спиридонов, А. И. Репина, Е. М. Карчевский
(27)	K 2 3 , 2 =	2n o G i (x,y) -               , x E r 2 , y E r i ,
		П о + n
(28)	K 23,3 =	dG i( x,y)    dG o( x,y) - Д 7 X — Д 7 X , X E Г 2 , y E Г 2 , dn 2 (y)       dn 2 (y)
(29)	3,4 K 2   =	=         G o (x,y)           G i (х,У), x E r 2 ,y E r 2 ,
		n i + n o            n i + n o
(30)	4,1 K 2   =	d 2 G i (x,y) " Л f       f \ , x E Г 2 , y E r i , dn i (y)dn 2 (x)
(31)	4,2 K 2   =	2П о dG i (x,y) , x E r 2 ,y E r i , П о + n i дп 2 (х)
(32)	4,3 K 2   =	d 2 G i (x, y) _ ^^Go Cx,^^     e r    e r dn 2 (x)dn 2 (y)    dn 2 (x)dn 2 (y), Ж      2 ,y      2 ,
	4,4	2n i   dG o (x,y)     2П о dG i (x,y)
(33)	K 2   =	П о + n i dn 2 (x)      n o + n i dn 2 (x) ,           2 ,        2

Пусть контуры Г 1 и Г 2 имеют формы окружностей радиусов a _i и a 2 , соответственно. Получим явные выражения для матричных элементов метода Галеркина. Выполним в (14) — (17) замены

W i (t) = a i U i (t),   W 2 (t) = a i V i (t),   W 3 (t) = a 2 U 2 (t),   W 4 (t) = a 2 V 2 (t).

Будем разыскивать приближения к функциям w k (t) в виде отрезков рядов Фурье вида

n

Wk(t) = ^ wmk)Фm(t),   к = 1,2, 3, 4, m=µ где д = 0, если в качестве базисных функций используются функции фт(^ = cos(mt), m = 0,... ,n, и д = 1, если в качестве базисных функций используются функции фm(t) = sin (mt), m = 1,...,n. Скалярное произведение определим, как

2π

^(u,v) = 2n j ^{u ( t ) v ( t )dT},

u, v ∈ L ₂ .

Применяя метод Галеркина, получим систему линейных алгебраических уравнений nnn

• (36)  W(1) + V him1)Wm) + V hzm2)w(2) + V hm^W^ + a l         lm m        lm mlm m

• m=^          m=^m

n

+ v h^wm=°,  l=м,..., n, m=^

(37)	1    (2) w a 1 l	n + V C-MS m=^	n + V m=^	(2 , 2) (2) h lm w m	n + V m=^	(2 , 3)   (3) h lm W m +
			+	n V h (i:“ m=^	(4) w m	°,     l — m, .. ■	,n

(38) 1   (3) w a2 l n + у /i(3’1)w(1) +    hlm Wm m=^ n +V m=^ (3,2)   (2) hlm wm n +V m=^ (3,3)   (3) hlm Wm + + n V him:“ m=^ (4) wm °,    l — m, .. ■ ,n nnn

(39) -w(4) + V h^w^ + V hm2V,2 + у ЦтМЧ l         lm m        lm m        lm m a 2

m=^          m=^m

n

⁺ V h^w m = °, l = м,..., n.

m=^

Матрица метода Галеркина является блочной матрицей второго порядка. Элементы левого верхнего блока имеют вид

_ р2п 2П hm = —     Kij УУфтХтУ^В'У'У n Jo Jo где i, j = 1, 2.

Элементы правого верхнего блока имеют вид

^   2n 2n hmj) = —           Kl’j (t2,т^^)фm(т2)фl(t1)dт2dt1, n 0    0

где i = 1, 2, j = 3, 4.

Элементы левого нижнего блока имеют вид

, (j _ £l Г Г ^i,ji,j ² 1         ¹А_ш,(12'\ат¹<11²

hlm = _n j J    K 2 ^(t 1 ,^T 1 )^фт^(т1 )^фl^(L2)^dт1 ^dt 2 ,

m, l = M, . . . ,n,

m, l = M, .. ., n,

m, l = m, .. ., n,

где i = 3, 4, j = 1, 2.

Элементы правого нижнего блока имеют вид

2п   2п                     ______ hi^ = ~           K2,j (t2,т2!)фm(т22)фl(t2)dT22dt2, m, l = ц,... ,n,

n Jo  Jo где i, j = 3, 4. Здесь щ = 1/2, если l = 0 и щ = 1, если l = 0.

Пусть расстояние между центрами окружностей Г 1 и Г ₂ равно d, радиусы окружностей равны а 1 и a ₂ , соответственно. Тогда матричные элементы метода Галеркина, согласно [20] , имеют вид:

h (1,1) _ in                  (1)l             i^                 (1)‘ hii    — 2 koJi\koa1)Hi   vkoa1)     2 kiJi\kia1)Hi \kia1), h^ =       ji(kia1)H«(^ - ^i. Ji(koa1)H(1)(koa1), ll       Hi + Ho         '                Hi + Ho            i hm3 = i2^ kHm) (ka2)(Jm-i(kr)Ji (ka1)(-1)(m-i) +

+ Jm+i(kir)J-i (kia1)(-1)(m+i+^)), hm4 = - np^. Hm1 (kia2) (Jm-i (kir)Ji(ki a1)(-1)(m-i) +

+ Jm+i (kir)J-i(kia1)(-V)Jm+l+^), hu’1 = i-^k2 Ji (koa1)Hi(1)‘ (koa1) - ^ Ji (kia1)Hi(1)‘ (kia1),

h (^{2 , 2)} = - + -JJJ^ k i J i (k i a 1 )H (1) ' (k i a 1 ) a 1    H i + H o

h ⁽³’³⁾ = iⁿk i J i (k i a 2 )H ⁽¹⁾ (^ 2 ) - i^koJi (k o « 2 ) Н ⁽¹ (k o a 2 ),

h(3’4) = inni Ji(koa2 )H(1)(koa2)inno_ Ji (kia2)H(1) (^2), П + По           l            ni + По           l hm,1) = - i2^k-j'm(kiai)(Hi(1)‘(kia2)Jm-i(kir)+

+ ( - 1) ^M H -¹_i⁾ (k i a 2 )J m+i (k i r) ) ,

h(„2) = innoai kijm(kia1)(H(1) (kia2)Jm-i(kir)+ im      ni + no                i

( - 1) ^ H -¹_i⁾ (k i a 2 )J m+i (k i r) ) ,

h (4’³⁾ = — k, ² J ' (k₄a₂)H(ka₂) - —kJ ' (k_oa₂)H (^1Y (k_oa₂), 2 i i i 2 i i 2         2 о i о 2 i o 2 ) ,

h(4’4) = - + i^^ koJi(koa2)H((1)' (koa2)- ll       a2    ni + no               l inno kij (kia2)H(1)(kia2), ni + no    l         l где m,l = ц,... ,n, oi = 1 /2, если l = 0, и oi = 1, если l = 0.

В наших расчетах мы исследуем поведение H- и E-поляризованных квази-WG мод, для которых нормированные частоты при d = 0 отличаются в 3-м разряде для случая H-поляризации, и во 2-м разряде для случая E-поляризации. А именно, в случае H-поляризации мы имеем следующие начальные точки при d = 0 : к = 9.9924, 7 = 6.07232 х 10 ^-7 и к = 9.9948,7 = 2.01306 х 10 ^-11 для дважды вырожденных мод (17, 2) и (21, 1), соответственно. В случае E-поляризации при d = 0 : к = 9.6112,7 = 5.01117 х 10 ^-7 и к = 9.6239,7 = 2.13596 х 10 ^-11 для тех же мод (17, 2) и (21, 1), соответственно. Радиус отверстия, нормированный по радиусу микродиска, зафиксирован r = 0.03. Мы заинтересованы в получении максимальной направленности излучения D, сопровождаемой относительно небольшим значением порога генерации γ (рисунок 2) .

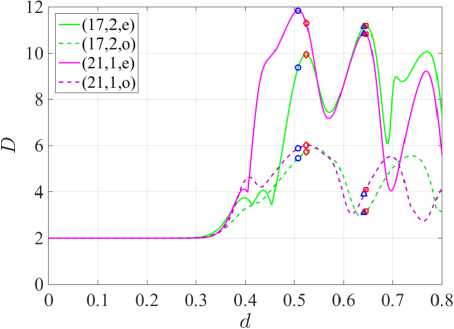
( а ) D при H-поляризации

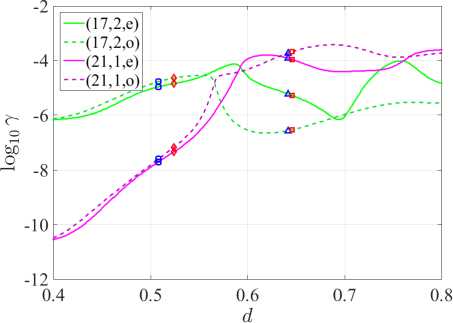
( б ) γ при H-поляризации

0    0.1   0.2   0.3   0.4   0.5   0.6   0.7   0.8

d

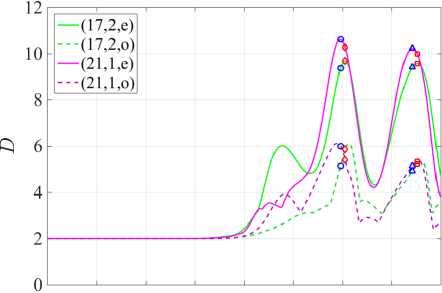
( в ) D при E-поляризации

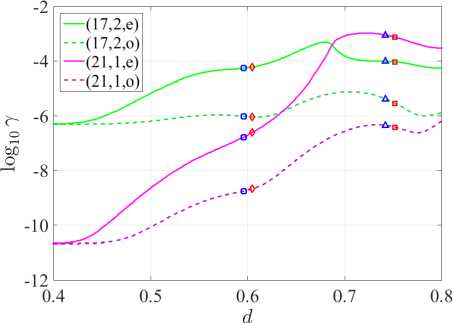
( г ) γ при E-поляризации

Рисунок 2. Зависимости направленности D и порога генерации излучения γ от параметра d

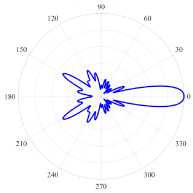
Определение D дано в [13, уравнение (46)]. Рисунок 3 помогает контролировать направление главного лепестка на диаграммах поля в дальней зоне (см. правые панели на рисунках 4 и 5) .

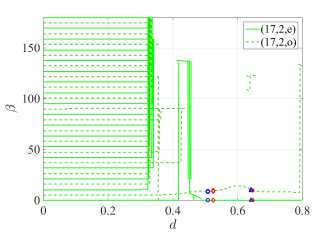
( а ) для моды (17, 2) при H-поляризации

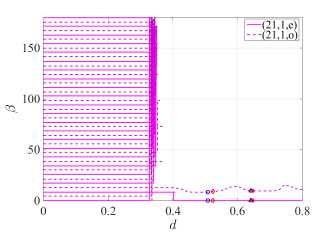
( б ) для моды (21, 1) при H-поляризации

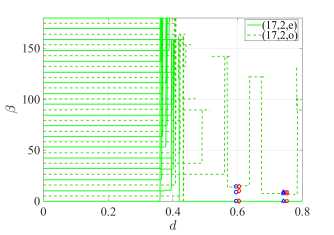
( в ) для моды (17, 2) при E-поляризации

Рисунок 3. Зависимости угла β максимальной направленности от d

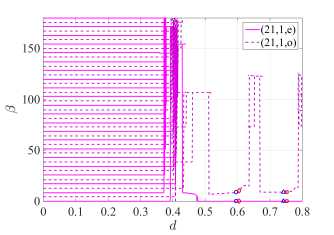
( г ) для моды (21, 1) при E-поляризации

Синие маркеры на рисунках 2 и 3 соответствуют первому и второму максимумам направленности моды (21,1, е), красные маркеры соответствуют аналогичным максимумам моды (17, 2, е). Для детального анализа мы выбираем первые максимумы D моды (21,1, е) и рассматриваем рисунок 4 в случае H-поляризации и рисунок 5 в случае E-поляризации. В случае H-поляризации при d = 0.51 мы имеем наибольшую направленность для моды (21,1,е), сопровождаемой относительно небольшим порогом γ . Порог этой моды самый низкий среди всех четырех исследуемых мод, а их нормированные частоты отличаются в третьем знаке. В случае E-поляризации при d = 0.599 нормированные частоты исследуемых мод отличаются во втором знаке,

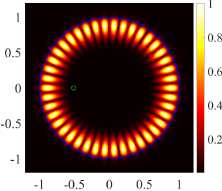
• ( а )    (17, 2, e), k = 9.9927, log ₁₀ (7) = -4.9457, D = 9.51

  
  
  
  
  
  

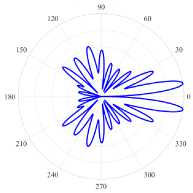
• ( б )    (17, 2, o), k = 9.9929, log ₁₀ (7) = -4.7586, D = 5.50

  
  
  
  
  
  

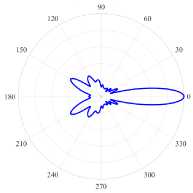
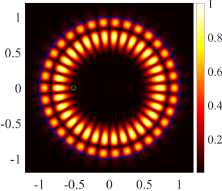
• ( в )    (21, 1, e), k = 9.9948, log ₁₀ (7) = -7.6640, D = 11.83

  
  
  
  
  
  

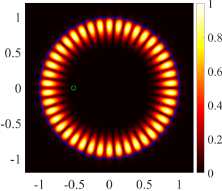
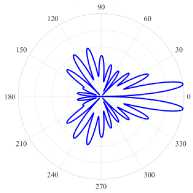
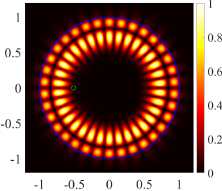
• ( г )    (21, 1, o), k = 9.9948, log ₁₀ (7) = -7.5550, D = 5.90

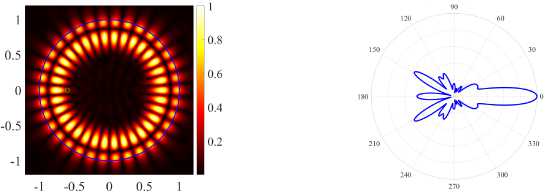
( а ) (17, 2, e), k = 9.6229, log ₁₀ (7) = -3.9864, D = 8.21

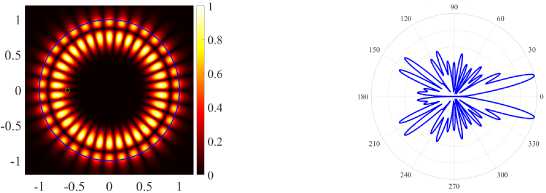
( б ) (17, 2, o), k = 9.6138.5, log ₁₀ (7) = -5.1499, D = 4.25

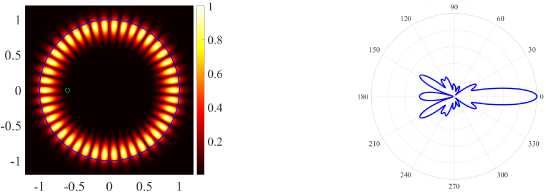
( в ) (21, 1, e), k = 9.6313, log ₁₀ (7) = -2.9738.5, D = 9.23

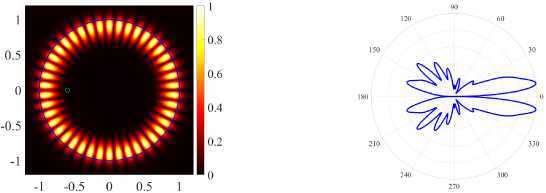
( г ) (21, 1, o), k = 96241., log ₁₀ (7) = -6.3621, D = 4.47

а наибольшую направленность имеет мода (21,1, е), однако порог моды (21,1, о) ниже порога моды (21,1, е).

Как в случае H-поляризации при d = 0.51, так и в случае E-поляризации при d = 0.599 мы получаем квазиоднонаправленное излучение для каждой из мод четного типа. Моды нечетного типа имеют два одинаково интенсивных лепестка при меньшем значении коэффициента направленности D . Увеличивая d, мы получаем графики K(d) и y (d), показанные на рисунке 6. Правые панели для y (d)

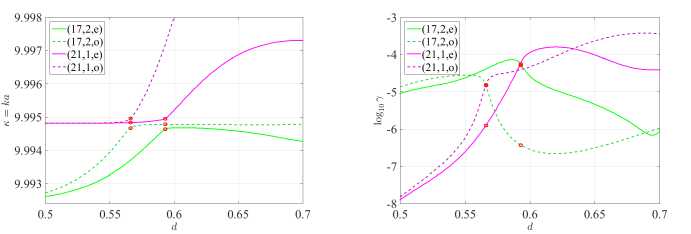
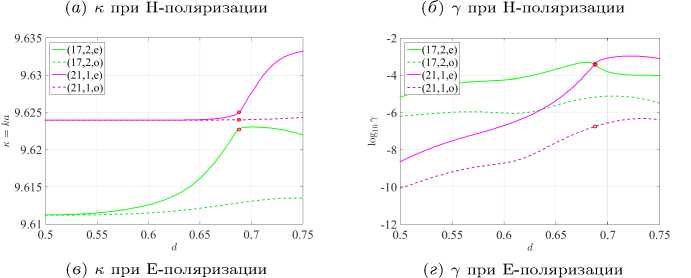
Рисунок 6. Зависимости нормированной частоты κ и порога генерации излученя γ от смещения отверстия d представляет собой увеличение участков [0.5, 0.7] и [0.5, 0.75] правых панелей рисунка 2, для H- и E-поляризаций, соответственно. Обратите внимание, что значения d = 0.51 и d = 0.599 лежат перед эффектами «avoided resonance crossing» для соответствующих поляризаций.

Когда частоты мод (17, 2, е) и (17, 2, о) начинают расти и приближаются к частотам мод (21,1, е) и (21,1, о), соответственно, на рисунке 6 мы наблюдаем эффект «avoided resonance crossing». Точнее, частоты мод избегают пересечения, однако значения порогов генерации γ все же пересекаются на рисунке 6).

Рассмотрим подробнее точки, в которых частоты избегают пересечения. Для H-поляризации d = 0.566 и d = 0.592, а для E-поляризации d = 0.688 (см. рисунки 6) .

Для каждого двухкомпонентного собственного значения (к, y ) мы имеем две ортогональные собственные моды (нечетную и четную). В [21] было высказано предположение, что «псевдорешетчатые моды» появляются, если собственные значения двух или более мод, принадлежащих к разным азимутальным семействам, приближаются друг к другу (по частоте) на плоскости (Re к, Im к). Того же можно ожидать и в LEP-анализе, на плоскости (к, y ).

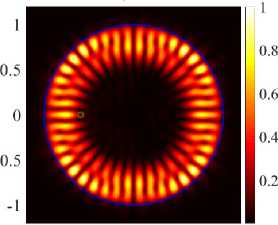
Известно также, что когда два собственных значения близки друг к другу и наблюдается эффект «avoided resonance crossing», происходит гибридизация полей мод [22] . Действительно, для H-поляризации в точке d = 0.566 (см. рисунок 7а) происходит гибридизация полей мод (17, 2, о) и (21,1, о), в точке d = 0.592 (см. рисунок 7б — гибридизация полей мод (17, 2, е) и (21,1, е).

Аналогично, для E-поляризации в точке d = 0.688 (см. рисунок 7в) происходит гибридизация полей мод (17, 2, е) и (21,1, е). При дальнейшем исследовании мы наблюдаем, что диаграммы поля в ближней зоне пар квазивырожденных мод в области сильной связи (контролируемой параметром смещения дырки d) приобретают формы, приблизительно равные сумме и разности полей двух рассматриваемых мод.

Наша цель — добиться квазиоднонаправленного излучения, однако мы видим, что в результате гибридизации исследуемые моды приобретают новые свойства. Мы называем их PJ усиленными WG модами, из-за специфических паттернов диаграмм поля в ближней зоне.

А именно, яркие пятна поля не обходят возмущенную область (дырку), а концентрируются вокруг нее. Природа этого явления, которое мы наблюдаем для четных мод, имеющих максимумы поля у дырки, может быть объяснена с помощью PJ эффекта. На рисунках 6а и 6б мы видим, что пороги мод (17, 2, о) и (21,1, о) пересекаются при d = 0.566. Отметим, что мода (21,1, е) не участвует в гибридизации, хотя ее частота близка к частотам гибридизируемых мод, поскольку она

(21, 1, o) - (17, 2, o),

κ = 9.9950, log ₁₀ (γ) = -4.8057

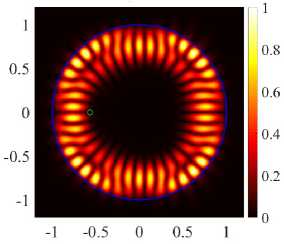
(21, 1, o) + (17, 2, o) κ = 9.944, log ₁₀ (γ) = -4.8291

1    -0.5    0    0.5     1

• ( а )    случай H-поляризации, d = 0.566

(21, 1, e) - (17, 2, e), κ = 9.9949, log ₁₀ (γ) = -4.2858

-1    -0.5    0     0.5     1

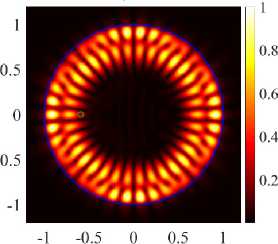
(21, 1, o) + (17, 2, o), κ = 9.9946, log ₁₀ (γ) = -4.2099

• ( б )    случай H-поляризации, d = 0.592

(21, 1, e) - (17, 2, e) κ = 9.6250, log ₁₀ (γ) = -3.3909

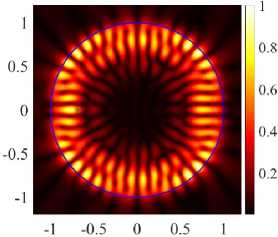
(21, 1, e) + (17, 2, e), κ = 9.6227, log ₁₀ (γ) = -3.4406

1    -0.5    0     0.5     1

• ( в )    случай E-поляризации, d = 0.688

Рисунок 7. Поле в ближней зоне гибридизированных мод принадлежит к ортогональному классу симметрии. Аналогично, для E-поляризации при d = 0.688 (см. рисунки 6в и 6г) пересекаются пороги мод (17, 2, е) и (21,1, е), а мода (21,1, о) не участвует в гибридизации. Гибридизирующиеся моды превращаются в сумму и разность двух квази-WG мод.

В случае H-поляризации в первой точке d = 0.566 нечетные моды начинают трансформироваться в моды ромбовидной и треугольной формы (см. рисунок 7а) , во второй точке d = 0.592 четные моды начинают трансформироваться в моды квадратной формы (см. рисунок 7б) . В случе E-поляризации в точке d = 0.688 четные моды начинают трансформироваться в моды шестиугольной формы (см. рисунок 7в) . На рисунках 7б и 7в наблюдается проникновение поля во внутреннюю область, максимумы поля не обходят отверстие. Во всех трех точках, где частоты избегают пересечения, порог одной из мод резко падает, а другой растет (см. рисунок 6) .

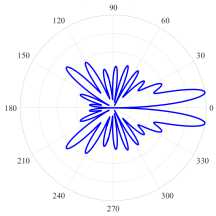
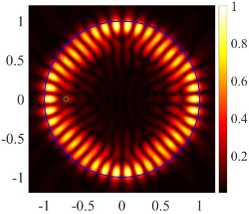
В точках, где частоты избегают пересечения, наблюдается обмен полями между соответствующими модами. После обмена полями для H-поляризации PJ усиленные WG моды (17, 2, о) и (21,1, о) становятся ромбовидной (см. рисунок 8) и треугольной формы (см. рисунок 8г) . Около второй точки для H-поляризации мы наблюдаем обмен полями для четных мод (17, 2, е) и (21, 1, е). Аналогично, для E-поляризации около точки d = 0.688 наблюдается обмен полями между четными модами (17, 2, е) и (21,1, е). После обмена полями моды (17, 2, е) и (21, 1,е) становятся ромбовидной (см. рисунок 9а) и шестиугольной формы (см. рисунок 9в) . Четные моды имеют более высокие значения направленности, кроме того, их излучение квазиоднонаправленное, что подтверждается нормализованными диаграммами поля в дальней зоне.

Исследуем собственные значения и направленность излучения после обмена полями мод (см. рисунки 8а — 8г для H-поляризации и рисунки 9а — 9г для E-поляризации). В результате нашего исследования для H-поляризации можно сделать вывод, что четная мода (17, 2, е) (см. рисунок 8а) имеет максимальную направленность при минимальном значение порога генерации в точке d = 0.694. В случае E-поляризации максимальную направленность в точке d = 0.72 имеет четная мода (21,1,е) (см. рисунок 9в) , однако порог моды (21,1,о) (см. рисунок 9г) меньше порога моды (21,1, е). Высокая направленность моды (21,1, е) обусловлена обратным эффектом PJ.

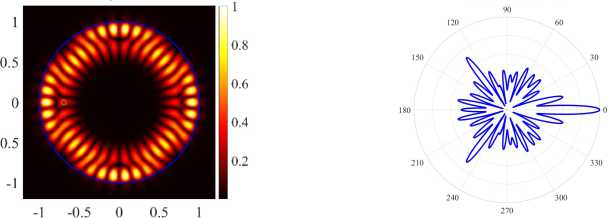
( а ) (17, 2, e), k = 9.9943, log ₁₀ (7) = -6.1656, D = 6.58

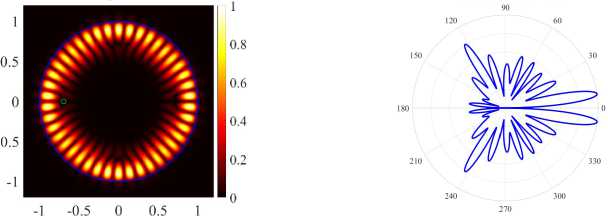
( б ) (17, 2, o), k = 9.9948, log ₁₀ (7) = -6.0355, D = 4.88

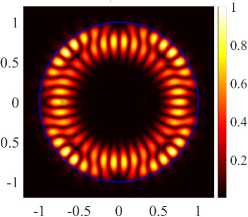
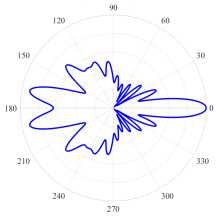
( в ) (21, 1, e), k = 9.9973, log ₁₀ (7) = -4.4054, D = 4.08

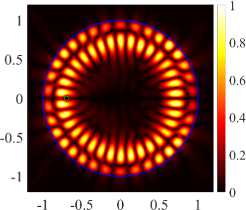
• ( г )    (21, 1, o), k = 10.0211, log ₁₀ (7) = -3.4314, D = 5.53

  
  
  
  
  
  

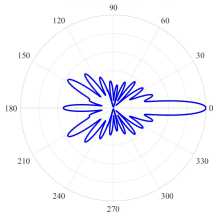
  ( а ) (17, 2, e), k = 9.6229, log ₁₀ (7) = -3.9864, D = 8.21

  

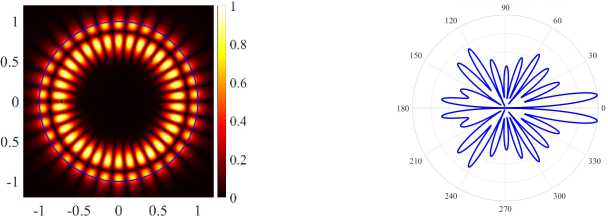
  ( б ) (17, 2, o), k = 9.6134, log ₁₀ (7) = -5.1499, D = 4.25

  
  
  

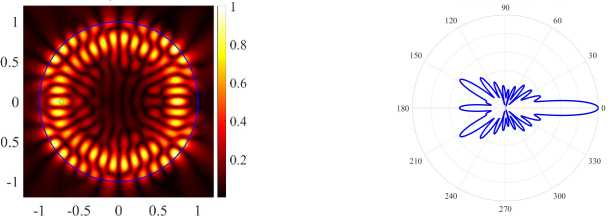
  ( в ) (21, 1, e), k = 9.6313, log ₁₀ (7) = -2.9734, D = 9.23

  
  
  

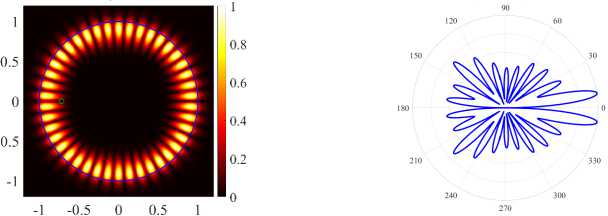
  ( г ) (21, 1, o), k = 9.6241, log ₁₀ (7) = -6.3621, D = 4.47

  
  

Заключение

Результаты наших численных экспериментов, выполненных с помощью тщательно протестированного программного комплекса, подтверждают предположения [21 , 22] о том, что можно управлять характеристиками порогового усиления и направленности микро-дискового лазера с помощью небольшого отверстия. А именно, мы обнаружили, что небольшое отверстие, просверленное во внутренней фокальной области микродискового лазера с высоким показателем преломления, приводит к усилению направленности излучения WG мод, при этом порог генерации излучения остается небольшим. В отличие от [21 , 22] , этот вывод основан на классической полноволновой электромагнитной теории и не использует биллиардную теорию или концепцию волнового хаоса. Таким образом, он обеспечивает простое и ясное инженерное правило для размещения отверстий.