Моделирование оптимального распределения воды в речных руслах и машинных каналах Аму-Занг

Основная часть . Данную задачу моделируем в предположение, что канал имеет дискретной раздачи (оттоки) к потребителям и вдоль канала непрерывно происходит фильтрация (рис.1.), Канал разделен на n участков, в каждом из которых вода расходуется либо только на фильтрацию, либо на фильтрацию и раздачи. При этом решение на конце n - го участка будет граничным условием ( n + 1 )-го участка. Расход раздачи ⁽ k )

обозначим через Q от . На участках, где раздачи отсутствует:

( k = 2 n + 1, n = 0,1,2...),    qO 4= 0, приравняем нулю. Для решения этой задачи используем дифференциальное уравнение вида [4,10]:

d ( a'u2 ^

a du  u da

--+--+-- g St g dt  dx ^ 2 g )

+   = in dx   0

—

u ²

_C 2 _R

—

a ( - V ) dQ   a ( u V ) dQ

gQ dt

gQ

dt

расходом вдоль пути). Впервые оно было выведено Г. А. Петровым и К.Ш. Латиповым [1,5,7]. В дальнейшим для простаты записи черточку в скоростях опускаем.

В этом уравнении а, а1, а2 •- коррективы количества движения, учитывающие лишь неоднородность для осредненных скоростей: а' -полный корректив кинетической энергии потока, учитывающий неоднородность поля осредненных скоростей и кинетическую энергию пульсаций. Потеря напора по длине канала выражением: [7]:

опредеяется следующем

.

dhf = i ‘ dx -

Q-dx = Q-f ( x ) dx

2         ТС

KM   KM

Полный уклон

i f ,   гидравлического

сопротивления в случае

турбулентного движения с переменным расходом вдоль пути зависит от потерь энергии на турбулентное трение между слоями осредненного dQ .

движения и от интенсивности изменения расхода -^-, ( Л - 1,2 ) .

dQ ,

Где ^Q функция dt , переменная вдоль потока; K M -модуль расхода; ^dh f -потери напора на сопротивление, обусловленное примущественно изменением живых сечений по длине и выраженное через потери напора на трение в естественных и искуственных водотоках.

Из анализа [3,5] полученных для потерь напора выражений были выведены некоторые формулы для уклона трения.Наиболее простой является формула [7]

o(u-V) dQ i f - i f ^~       -- U f f     gQ    dx

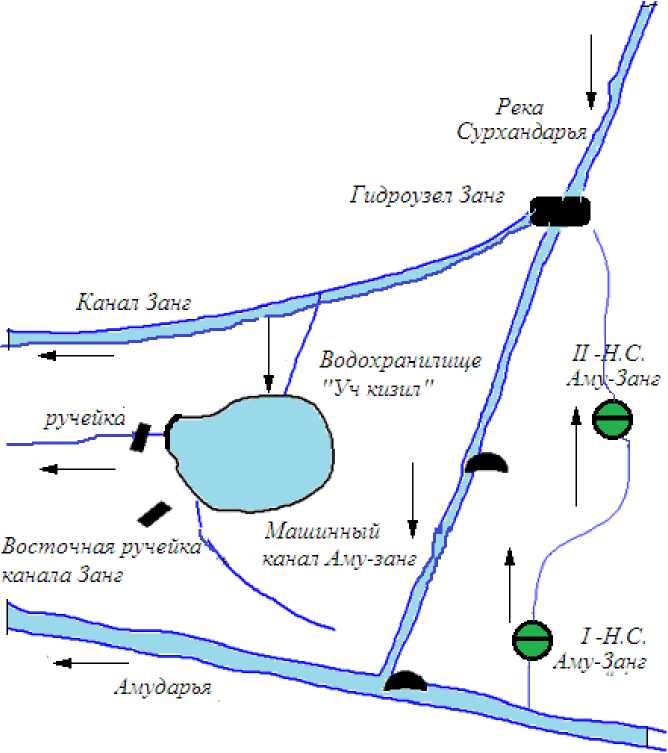
Рис.1.Схема водохранилища Учкизил и машинного канала Аму-Занг.

Согласно, (3) формуле, потере напора при движении жидкости с переменным и постоянным расходами отличаются на некоторую вели- чину, определяемую вторым членом правой части. При практических расчётах для уклона трения используется приближенная формула:

Qu

i f = --Г f (Х )='

f  K2

Ордината уровня свободной поверхности равна

,        ду    д h    д z

У = ^h + ^z ,     = ^ ⁺ ^ = ~- i о .

дx  дx  дx

Для произвольного k – участка уравнение (1) имеет вид:

ak) дuk , uk до^ + _dja‘k)u Yhkk = g  дt   g  дxk   дxk [  2 g )  дxk

( ( k ) ^L ₊ °B^ vl 'Qt a -(u . V . ' dQ )

⁰    C k² R k         Q k        д x k          Q k         dt

При     для

a^{( k} ) « a ^{( k} ) « a ( ^kk ) « a’ ^k )

произвольного

k –

участка

при

= const . имеем уравнение (1).

В случае медленно изменяющегося движения потока на практике принимается приближенно a « a ~ a₂ « a' = const . Однако и общем случае для них существует ряд выражений, например полуэмпирические формулы для a [1,3,5]:

_a _ ( 1 + k i ) 2 ( 1 + k ₂ ) 2

( 1 + 2 k )( 1 + 2 k ₂)

где

- = ^ g

¹ К C ,

л

k 2 = 2 k 1 1

b ^

—

к

К =-----+ 0,314 - параметр Кармана; и

C

для a' = 3a — 2 +1,92

^{C 2}

При решении уравнение (1) воспользуемся уравнением неразрывности и напишем в форме:

^k- + ^ = -^ ^-S'^ k ) a t           q *

где q(k) - потери воды на фильтрацию в k -ом участке, приведен-^k        1 + (— 1)k ные к единице длины канала: о- = —, о- =--------забор воды на боковой

L _k         2

отток, приведенный к единице длины бокового русла. Если на рассматриваемом участке трассы транзитный расход воды равен Q _н , то, согласно (7),

k

k

Qh = qH ^k ) — Z x^ ’ ’ — E ^O m ) x .

n = 1

n = 1

В коротких каналах, например в ручейках водохранилище

«Учкизил» рис.1. или при

малом

q ( - ' = о

( u k — V k ' ) dQ k )

изменении расхода на фильтрацию

^Qk      ^{d x}k

= 0 .

В

место

уравнение (6) можно использовать

упрощенное уравнение du,       u, du,

—- + u,——- ^d t      g ^d x_k

d h

i- g /' = g i dxk

( - )

u k

к

⁰    CR k J

д'М — V ) dQ ( k )

I k \ k       k /    omU tit

Q k

dt

Уравнение неразрывности (7) также упрощается d^₊<=-. ? jk )

s t ⁺ a x     ° ^k q o"

Уравнения (9) и (10) могут быть использованы и в отсутствие фильтрации из каналов на пример Сурхандарьи. Однако эти упрощения незначительно облегчают численное решение уравнений.

Для определения потерь воды на фильтрацию из трассы канала k -го участка неравномерного движения используем формулу Павловского:

q фк ) = к 1 ^k 'B к ' + 2 h^{1 k} ) )             (ii)

где B ^ ) - ширина к -го участка канала по урезу (рис.2); K 1 ^{( к} ) -коэффициент фильтрации k -го участка канала. Тогда скорость фильтрации определится как:

K^k )

V¹^ ’ =     №) + 2 h^k ) )                 (12)

Хк здесь хк -смоченный периметр к -го участка канала. Скорость отделяющихся масс за счет боковых оттоков [5, 6] равна:

V = Г} * ) COS ^ k     om       k

,

О{к) кА к)      от от = ^к)

где З _к — угол между направлениями скоростей уходящей массы и к )

основного потока; ^С 7 — площадь живого сечения оттекающего потока в k -м русле, определяемая в случае призматических русел по формуле ^е )= ^к + m zk)z-                   (14)

здесь z _k высота открытия затвора, которая меняется в пределах 0 <  7_к <  h ⁽ ) . Из (6) и (14) получаем выражение для расходов за счет фильтрации в единицу времени:

dQ _Ф dt

= K f ) uM ^}+ 2 h⁽ ) ) + 2 ( т_к + 1 ).

xk

(д h ^{( к} )       д h^{( к} П’

⁺ u-  ;

д t          дх,

\                   К у _

Чтобы

производные

вычислить расход на k -м участке трассы, выразим дuk     дик и    через расход воды. Уравнения (6) умножим на дt      дхк юк и произведём некоторые преобразования, используя выражения (12) -(15) для призматических каналов.

Уклон свободной поверхности k -го участка канала I , определяется по формуле

Qh ( к )

- градиент глубины наполнения; Q^ = ^к zk b0 0) + тк0 zk \l2 gzk - м3

расход воды на боковых оттоках (—) (рис.1.), где ^ k - коэффициент сек

1^      Z k

;

расхода, определяемый зависимостью [7] ^ _к = 0,62 ^ 1 - 0,12

i <  ‘ >=1 ₊⁸-^

i 0     I + n dxk

- градиент глубины наполнения;  QO‘1 = Vkzk (bk0'+ mk zk \j 2 gzk - расход воды

м ³

на боковых оттоках (   )

сек

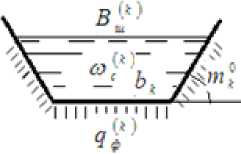
Рис.2. Площадь живого сечения оттекающего потока

(рис.1.), где   v_k —   коэффициент расхода,

определяемый       зависимостью       [7]

С

V = 0,62 | 1 - 0,12 - z k )

k

h^(k )

Распределение боковых расходов определялось методом случайного поиска и проверялось по критерию

0 <  Q ^{( k} ) <  Q^(k )

om      n

где Qnk) — потребность k - го участка. Выявлено, что полученные результаты совпадают с данными наблюдений и условие сходимости устойчиво выполняется. Конечные величины уточнялись за третьим знаком после запятой, и погрешность практически не превышала 2,5%. Расчеты проводились при следующих исходных данных: g = 9,81 -м,HM = 2м в = 1,13472,0k = П K

k	Lk , м	^k , м2	3 Q ’k 1, -с	h(k), м	zk,м	а (k) — Чф , с	3 Q<.k 1, -с
1	1000	41,48	40,32	1,882	0	0,59	0
2	1,5	40,68	39,05	1,789	0,38	8,9.1-	1,25
3	700	40,47	38,77	1,783	0	0,28	0
4	1,0	39,58	37,51	1,767	0,44	5,81	1,25
5	1120	39,09	36,60	1,749	0	0,91	0
6	0,5	37,95	35,35	1,718	0,54	2,5.1-	1,25
7	1000	37,54	34,79	1,706	0	0,56	0
8	2,5	36,50	33,52	1,675	0,30	1,4.1-	1,25
9	1500	35,66	32,40	1,645	0	1,12	0

Точность и правильность приведенного алгоритма оценивалась сопоставлением машинных данных с данными [1,5,11]. В частности, при k = 1 установлена правильность построенного алгоритма расчета. Анализ результатов расчета подтверждает, что алгоритм может быть использован при решении задач оптимального управления распределением водных ресурсов магистрального канала между боковыми отводами при различных дефицитах.

Выводы:

• 1.    Использование решений гидравлики открытых бурных плановых потоков (методы Н, Т. Мелещенко и Ф. И. Франкля) допустимо для весьма приближенных оценок гидравлических характеристик потока в приделах рассмотренной конструкции водосброса с боковым сливом и отбросом потока в русло нижнего бьефа (ВБТ).

• 2. Использование методов расчета боковых водосливов неприемлемо без дополнительных усовершенствований и разработок для практических ^расчетов водосброса с боковым сливом и отбросом потока в нижний бьеф.

• 3. Решена задача оптимального распределения воды между потребителями с учетом забор воды для орошения, фильтрация, испарение и. т. д. – т.е. потеря вдоль трассы каналов

• 4.    Получен аналитическое выражение и составлен алгоритм расчета оптимального управления распределением     водных ресурсов

• 5.    Анализ результатов расчета подтверждает, что алгоритм может быть использован при решении задач оптимального управления распределением водных ресурсов магистрального канала между боковыми отводами при различных дефицитах.

магистрального канала.