Моделирование ориентационных явлений около частиц наполнителя в полимерных нанокомпозитах

Our work considers the problem of modeling the oriented regions formation near the filler particles in polymer nanocomposites. Hypothesis was suggested that the growth of orientation regions is due to the extension of the orientation state of polymer to the neighboring non-oriented regions. A mathematical model has been developed to describe this phenomenon. The model is based on the assumption that the time evolution of the orientation tensor is determined by two factors: (i) mutual influence of orientations of polymeric chain links which are located in neighboring regions, and (ii) thermo-fluctuation growth of the chaos in the polymer link orientation.

Важную роль в формировании свойств полимерных нанокомпозитов играют слои около частиц наполнителя, имеющие размеры от двух до десяти и более нанометров [13]. Несмотря на многочисленные попытки определить причину их формирования и механические свойства, многое все еще остается неясным. Высказана гипотеза, что полимер в этих слоях находится в особом ориентированном состоянии. Но не предложена математическая модель образования этих слоев. Целью данной работы является построение такой модели.

Тензор ориентации звеньев полимерных цепей

В первую очередь, при построении математической модели, необходимо определить, с какими математическими величинами следует работать. Нам нужно иметь информацию о преимущественной ориентации звеньев полимерных цепей. Для этого разумно использовать тензор τ _j ⊗ τ _j , в котором символом τ _j обозначен единичный вектор, определяющий направление ориентации в пространстве j -го звена. Индекс j принимает значение номеров всех звеньев всех цепей, попавших в рассматриваемый объем материала. Данный тензор удобен тем, что можно найти его осредненное значение для всех звеньев полимерных цепей в рассматриваемом объеме, и результат этого осреднения не будет равен нулевому тензору. Он дает представление об ориентированном состоянии полимера. Собственные векторы и собственные числа его имеют понятный физический смысл. В дальнейшем мы станем называть тензором ориентации результат осреднения по множеству возможных состояний полимерного звена в данной точке тензор τ _j ⊗ τ _j с учетом частоты (вероятности) его появления и будем обозначать его символом O . Собственные векторы осредненного тензора τ _j ⊗ τ _j определяют направления в пространстве, вдоль которых в основном ориентированы звенья цепей, и направления, вдоль которых звенья ориентируются редко. В свою очередь собственные числа этого тензора дают количественную информацию о степени ориентации звеньев полимерных цепей в соответствующих направлениях.

Будем полагать, что энергия взаимодействия i-го и j-го звеньев полимерных цепей записывается в виде потенциала, сходного с потенциалом Леннарда – Джонса с единственным отличием: вместо скалярных величин в него входят тензорные величины, кото- рые определяют зависимость энергии взаимодействия звеньев полимерных цепей от угла между ними, с (I Л(I A c (1 Л c (1

u„ = —u" —T ® т • —т, ® t, = —u — (т,- - t.) = —u —т,. ®т,. -т, ®t, , ij              6                i i                     j j 6                  i j                 6                i i j j r3              3              r3

ij                                                                                                ijij где uij — взаимодействия i-го и j-го звеньев, Cu — константа материала, I — единичный тензор.

При моделировании процесса формирования ориентированных областей полимера можно использовать континуальные, дискретные и вероятностные модели. Рассмотрим их.

Континуальное, дискретное и вероятностное моделирование

КОНТИНУАЛЬНЫЕ МОДЕЛИ. Наиболее удобными для моделирования изменения состояния полимера при удалении от поверхности наполнителя являются континуальные модели. Они наиболее просты и позволяют быстро получать решения задач и проводить анализ физических процессов. В континуальных моделях полагается, что тензор O изменяется плавно. Он является непрерывной дифференцируемой функцией координат. В основе моделирования лежит предположение о том, что можно сформулировать дифференциальное уравнение в частных производных, которое позволит вычислять распределение тензора ориентации в пространстве для всех моментов времени. В континуальных моделях не рассматриваются отдельные звенья полимерных цепей и сами цепи. Это означает, что в них нет понятия вектора т j , и тензор т j ® т j в континуальных моделях не имеет смысла. Всю информацию об ориентации звеньев полимерных цепей несет в себе тензор O . Вводится он в модель как некоторая феноменологическая тензорная величина.

Влияние соседних звеньев на ориентацию полимера в рассматриваемой точке пространства можно определить в континуальной модели, используя тензор O . Другого способа в них не существует. Обозначим символом O continuum значение величины, полученной при осреднении O по соседним областям материала. Разница между тензором ориентации O в рассматриваемой точке и тензором влияния соседних частей материала O continuum позволяет строить уравнение эволюции во времени тензора O . Чем выше отличие между тензорами O и O continuum , тем сильнее стремится материал изменить текущее состояние и прийти к самосогласованному равновесному состоянию. В основе этого утверждения лежит гипотеза, что в равновесии осредненный по множеству возможных состояний тензор т j ® т j должен совпадать с тензором, осредненным по пространству. Этот момент будет уточнен ниже.

Введем понятие тензора O continuum следующим образом:

O

continuum

= C V rOx + Ax) dv, ⁶

Vr где dV = dAx 1 dAx2 dAx3 и условие нормировки формулируется равенством

C v f 4г dV = 1.

_V r ⁶

Тензор Ocontinuum в точке пространства, положение которой задается вектором x, равен интегралу по объему пространства V, занимаемому полимером за исключением малой сферической окрестности рассматриваемой точки пространства. Обозначим радиус этой малой окрестности символом r* . Исключение из интегрирования малой сферической окрестности связано с тем, что в ней не могут располагаться одновременно два звена полимерных цепей и поэтому взаимодействие между звеньями, расположенными на расстоянии, меньшем r* , невозможно. Текущей переменной в подынтегральной функции является вектор ∆x = ∆x1 i1 + ∆x2 i2 + ∆x3 i3 , символами i1 , i2 и i3 обозначены единичные базисные векторы прямоугольной декартовой системы координат. Под интегралом стоит тензор O(x + ∆x) в точке пространства, положение которой задается вектором x + ∆x с заданным весовым коэффициентом. Этот весовой коэффициент учитывает вклад в формирование тензора O(x) частей полимера, отстоящих от рассматриваемой точки на расстояние r = 'J∆x ⋅ ∆x . В качестве весового коэффициента мы используем выражение r-6 . Именно с такой скоростью убывает взаимодействие между звеньями полимерных цепей в рассматриваемой нами модели. Следовательно, именно такой вклад могут вносить тензоры ориентации соседних точек в формировании ориентированного состояния полимера в рассматриваемой точке пространства.

ДИСКРЕТНЫЕ МОДЕЛИ. В континуальные модели необходимо ввести информацию о реальной физике рассматриваемых явлений. Взять ее можно из моделей, которые непосредственно описывают движения отдельных звеньев полимерных цепей, позволяют исследовать взаимодействие их друг с другом. Делается это с помощью методов молекулярной динамики. Такие расчеты требуют выполнения огромного числа операций, занимают много времени, требуют огромной памяти компьютера. Поэтому разумно использовать молекулярную динамику не для расчетов физических процессов, а для обоснования правильности более простых моделей и способа вычисления нужных нам величин. А сами исследования лучше проводить с помощью более простых континуальных моделей.

Назовем дискретными моделями такие, в которых рассматривается движение всех звеньев всех полимерных цепей. К ним относятся молекулярная динамика, динамика диссипативных частиц и т. д. Особенностью таких моделей является следующее. В результате их использования в любой момент времени для любого звена полимерной цепи нам известен вектор ориентации τ _j и можно вычислить среднее значение тензора τ _j ⊗ τ _j .

В дискретных моделях значение тензора влияния соседних звеньев полимерных цепей на рассматриваемое звено получается в результате простого суммирования тензоров τ _j ⊗ τ _j с заданным весовым коэффициентом r_ij ^{- 6} ,

O

discrete

N

=CN ∑ j=1, i≠j

τ _j ⊗ τ _j

6,

Г- ij

где N — число всех звеньев. Требование нормировки формулируется равенством

N

C N ∑ ¹6 = 1.                                  (3)

j = 1, i ≠ j ^rij

Символом r_ij обозначено расстояние между центрами масс звеньев с номерами i и j . Полагается, что номер i имеет звено, центр масс которого расположен в рассматриваемой точке пространства, положение которой задается вектором x . Как и в континуальных моделях в качестве весового коэффициента мы используем выражение, которое

Моделирование ориентационных явлений около частиц наполнителя в полимерных нанокомпозитах определяет скорость убывания взаимодействия между звеньями полимерных цепей в рассматриваемой нами модели.

ВЕРОЯТНОСТНЫЕ МОДЕЛИ. К классу вероятностных моделей относятся модели, использующие для описания движения стохастические уравнения, распределения Гиббса плотности вероятности состояния и т. д. У вероятностных моделей есть важная отличительная особенность. В них не рассматривается движение всех звеньев всех полимерных цепей на всем интервале времени. Выбирается только одна или несколько цепей, а влияние остальных заменяется их эффективным действием и формулируется с помощью теории вероятностей или с помощью теории случайных процессов. В результате использования данного класса моделей мы имеем в каждый момент времени вероятность центра масс рассматриваемого i -го звена находиться в той или иной точке пространства с той или иной ориентацией. Поэтому определять тензор ориентации O в рассматриваемой точке пространства, положение которой задается вектором x , целесообразно путем вычисления математического ожидания тензора т i ® т i .

^O probability    O ( x ) = ( т , ® т , ) .

В данном случае используется осреднение по вероятности состояния системы. Взаимодействия между цепями учитываются при вычислении плотности вероятности состояния системы для рассматриваемого момента времени.

Для того чтобы иметь возможность связывать друг с другом континуальное и дискретное описание процессов, необходимо использовать гипотезу их эквивалентности. Сформулируем ее в следующем виде:

O

continuum

=O

discrete .

Как было уже отмечено выше, в неравновесных условиях тензоры O continuum и O _probability не равны друг другу. Чем выше это отличие, тем более неравновесным является состояние материала. И, наоборот, в положении равновесии выполняется равенство,

O

continuum

= O

discrete

= O

probability .

Основные причины изменения тензора ориентации во времени

Для построения модели, описывающей формирование во времени слоев около частиц наполнителя в эластомерном нанокомпозите, используем следующее предположение. Считаем, что есть две причины изменения во времени тензора ориентации в рассматриваемой точке пространства: а) из-за ориентирующего влияния соседних точек среды на рассматриваемую точку; б) из-за влияния теплового движения полимерных цепей, которое стремится привести материал в состояние с отсутствием ориентации. С учетом этих двух причин эволюционное уравнение может быть записано в виде

D O Dt

= a l C V J

V

O ( x + A x ) r ⁶

dV - O + a 2

- - O

, (6)

где D/Dt — объективная производная по времени, a1 и a2 — неотрицательные функции параметров состояния среды. О первом слагаемом в правой части уравнения речь уже шла выше. Чем больше различаются тензоры O и Ocontinuum друг от друга, тем быстрее материал стремится изменить данное неравновесное состояние. Другими словами, чем сильнее отличие ориентации от той, которую навязывают данной точке соседние точки, тем скорее идет изменение ориентации в данной точке в направлении к той, которую требуют от нее соседние точки. Второе слагаемое демонстрирует отклонение текущего состояния от состояния полного хаоса в ориентации звеньев полимерных цепей. Чем сильнее отличие ориентированного состояния полимера в данной точке от состояния полного хаоса (состояния без ориентации), тем сильнее тепловое движение стремится вывести материал из этого состояния, разрушить имеющуюся ориентацию звеньев полимерных цепей.

Преобразуем уравнение (6). Для этого нужно записать в более удобном виде первое слагаемое в квадратных скобках в его правой части. Разложим для этого тензорную функцию O(x + Ax) в ряд Тейлора и отбросим в ней члены третьего и более высоких порядков малости. Возможно это потому, что подынтегральная функция содержит множитель r6, который делает практически не влияющим на результат интегрирования все значения функции O(x + Ax), кроме малой окрестности точки пространства, положение которой задает вектор x. Вынесем за знак интеграла независимые выражения. В итоге получится формула г O(x + Ax)

C V J    /

Vr

г 1 „   dO    1ЛЛ dV CVJ / O + Z;Avi + 2^^

V r           i = 1 ^d x         2 i = 1 J = 1

V

8 2 O л л

A x A x d x i d x_J    i ^J

dV =

\

C

= o | c , J 4 dv | + ]T |° ( c , V V r 7 i = 1 ^x i V

f A x ,, ,J 1-Л^ J -t^{d' +}^Z

V r 7    ² i = 1 J = 1

d 2O dxi dxJ

c, J

V V

Axi Ax r6

dVV

Учитывая условие нормировки (7) и равенство нулю интегралов с нечетными подынтегральными функциями, получаем равенство

C„| ^{O ( x + A x} ) dV = O + C a£ I^{2 0}*,                   (7)

V r                         i=1 dx, где

C A = ¹ C v J ^A x² dV >  0. (8)

2 _V r ⁶

В итоге уравнение (6) принимает вид

D O Dt

= aa ₂

C«2

i = 1

a ² o d xi²

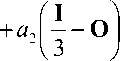
где a a = —.

a ₂

Конкретизация вида функций a и a2

Для решения задач формирования ориентированных слоев около частиц наполнителя в полимерных нанокомпозитах необходимо задать конкретный вид функциям a и a ₂ . Покажем, как можно определить функцию a , используя для этой цели математический аппарат равновесной статистической физики. В положении равновесия тензор ориентации O вычисляется с помощью распределения Гиббса.

⁰ = < у ® т ) = j t ® ^т C exp

Г

к

N

Z u , j = 1, № j

c B ⁹

d Г,

где С — нормировочная константа, c_B — постоянная Больцмана, θ — температура, Г – фазовое пространство координат элементов рассматриваемой системы. Нашей целью является получение уравнения, которое определяет ориентированное состояние системы в положении равновесия. Подставив в распределении Гиббса значение энергии взаимодействия звеньев полимерных цепей, получим выражение

Γ

c_B 9 к B

N

Z C j=1, ^ j r ij

\

d Γ .

Требование эквивалентности континуального и дискретного описаний (4), условие нормировки (3) и равенство (7) позволяют нам записать зависимость

N

Cn Z

j = 1,zj

T ■ ® T ■ jj

j

d 2 0

= O + CaZ i=1 5x,

с помощью которой выражение (11) принимает вид

^O = j ^T i v ^{T C} exp

Γ

^{1    C}u

к c B 9 C n к

¹ - T, ® T, ₃

{о+caZ f2O к           i=1 5x,

d Γ .

Далее необходимо воспользоваться равенством тензоров Ocontinuum и Oprobability ловиях равновесия (5). С учетом равенства (7) перепишем уравнение (12) в виде в ус-

^O + ^C a ZtT = j ^T i ^{0 T} i^C exp i = 1 о x _{z      r}

¹ C u

к c B 9 C n к

3 ^{- T} i ® ^T i

■f о + C a Z 1⁰

к            z = 1 5 x,

d Γ .

Нетрудно убедиться, что оно имеет решения d O

O + CA Z % 2 = A k ’ i dXi где Ak — тензоры, зависящие только от температуры среды. Они определяются как решение интегрального уравнения

f 1 C f 1 Ak = [tz ®TZ. C exp1 -k г             к cB9 CN к3

7^

^{- T} z ® ^T z ■ A k I ⁷ 7

d Γ .              (15)

Таким образом, мы пришли к следующему заключению. Равновесная статистическая физика говорит нам о том, что в положении равновесия должно выполняться равенство (14). Но мы сформулировали раньше уравнение эволюции тензора ориентации в рамках континуального описания процесса (9). В условиях равновесия оно принимает вид

a

C a Z

6 x_z.²

+1 - O = 0 .

Естественно, что оба эти уравнения (14) и (16) должны быть эквивалентными. Это возможно в том случае, когда функция a задана специальным образом. Найдем из требования эквивалентности равенств функцию a . Для этого исключим слагаемые со вторыми производными по координатам из (16) с помощью (14). В результате получим зависимость

a ( A k - O ) + 3 - O = 0.

После скалярного умножения этого равенства слева на тензор O получаем a ( O • A _k - O • O ) + 3 O • I - O • O = 0.

Используя равенство O • I = 1, которое является следствием определения тензора ориентации, получаем искомое значение функции a, a=

¹ - O • O

O • A _k - O • O

При этом следует из множества возможных значений тензоров A _k выбирать только те, которые дают неотрицательное значение для функции a . Решений уравнения (15) может быть несколько. Они соответствуют разным видам возможного ориентированного состояния среды (одноосного ориентированного состояния с тем или иным направлением оси ориентации, двуосного ориентированного состояния с тем или иным направление нормали к плоскости ориентации и т. д.).

Для завершения формулировки уравнения (9) необходимо указать, какой вид имеет функция a ₂ . Для этого необходимо вспомнить, что в уравнении (6) второе слагаемое учитывает рост хаоса в результате теплового движения. Стоящий перед ним сомножитель a ₂ определяет характерное время этого процесса. Для него целесообразно использовать обычное термофлуктуационное выражение

( a 2 = exp

V

U

+ C g

C b 6     ⁶

A

где коэффициенты U ₆ и C ₆ зависят от природы и структуры полимерного материала.

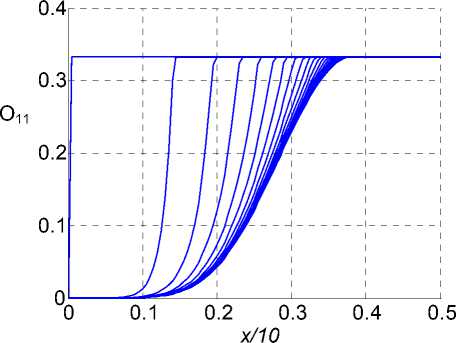
Рис. Зависимость компоненты тензора ориентации O ₁₁ от расстояния до поверхности наполнителя x, построенная с шагом по времени, равным 1 мин

Заключение

Один из примеров применения теории к моделированию процесса формирования двухосно-ориентированного слоя около поверхности наполнителя показан на рисунке. В данной статье не обсуждаются конкретные детали постановки задачи и осуществления расчетов. Подробное их изложение планируется осуществить в отдельной статье. Укажем только, что решение получено для одномерной задачи. Оно подтверждает, что предложенный в работе подход позволяет получать удовлетворительное описание исследуемого процесса.

Работа выполнена при поддержке Российского фонда фундаментальных исследований (гранты № 05-08-33361, № 06-03-32461, № 04-01-97505-р_офи).