Моделирование отклика сибирского радиогелиографа на спокойное Солнце

Исследование слабых по энергетике событий на Солнце актуально по причине их большого числа, что позволяет более достоверно выявлять статистические закономерности солнечной активности. К тому же общее уменьшение уровня солнечной активности в текущем цикле позволяет наблюдать события, которые в периоды высокой активности маскируются более мощными событиями. Интерес к слабым по энергетике событиям вызван тем, что, по некоторым предположениям, нагрев солнечной короны происходит в результате большого количества слабых солнечных вспышек, возникающих практически непрерывно [Parker, 1988; Knizhnik et al., 2018]. Поэтому вопрос о том, сколь слабые вспышки могут быть обнаружены путем наблюдения микроволнового излучения солнечной короны, также актуален. В данной работе анализируются инструментальные особенности многочастотного Сибирского радиогелиографа (СРГ), созданного при модернизации Сибирского солнечного радиотелескопа [Grechnev et al., 2003; Lesovoi et al., 2012, 2017]. Наиболее чувствительными по плотности потока микроволнового излучения данными СРГ являются так называемые корреляционные кривые (КК) — суммы модулей комплексных коэффициентов корреляции сигналов от пар антенн СРГ [Lesovoi, Kobets, 2017]. Эти кривые удобны и при исследовании динамики солнечной активности в течение дня или день за днем. Удобство обусловлено компактностью представления данных и высокой чувствительностью — до 0.01 с.е.п. (солнечных единиц потока). Однако КК меняются во времени не только вследствие изменения плотности потока падающего излучения. Причиной изменения КК может быть изменение пространственной структуры источников микроволнового излучения или диаграммы направленности (ДН) СРГ. Вариации КК во времени, вызванные изменением ДН, могут быть немонотонными и поэтому могут маскировать слабую солнечную активность. Наиболее контрастно вариации КК проявляются при отклике на солнечный диск, их уровень может достигать 0.1 %, что соответствует плотности потока излучения 0.5–1.0 с.е.п. в зависимости от рабочей частоты. Уровень отклика от компактных источников обычно составляет несколько процентов, поэтому влияние вариаций КК на такой отклик малозаметно. Однако при исследовании сверхслабой солнечной активности нужно корректировать отклик с учетом этих вариаций. Для коррекции вариаций КК, вызванных изменением отклика на солнечный диск, из полного отклика нужно вычесть этот отклик. Пример вариаций КК представлен на рис. 1. Отмеченные овалом «холмики» на двух кривых, соответствующих высоким частотам, проявляются на других частотах в виде более плоских участков или даже участков с общим длительным повышением уровня отклика. На рис. 2 показано, как эти вариации наблюдаются в течение года. Светлые дуги, расположенные симметрично относительно кульминации, соответствуют вариациям КК, отмеченным овалом на рис. 1. Во время слабой активности такие вариации хорошо заметны. С появлением активных областей, даже в отсутствие вспышек, вариации КК маскируются шумами активной области. В этом случае особенно важно подавить такие вариации, чтобы не спутать их с откликом на шум активной области.

В данной работе мы предлагаем метод моделирования корреляционных кривых как отклика СРГ на излучение спокойного Солнца. Модельные КК больше всего похожи на реальные КК в предположении, что край солнечного диска размыт. Суть метода заключается в том, что каждая точка КК рассчитывается как сумма определенного набора значений функции видности солнечного диска. Соответствующие значения функции видности солнечного диска определяются временем наблюдений и рабочей частотой СРГ. Факторами, влияющими на результат, являются радиус диска спокойного Солнца, степень размытости края солнечного диска, модули коэффициентов передачи антенн и влияние взаимного затенения антенн СРГ.

ОТКЛИК СРГНА СОЛНЕЧНЫЙ ДИСК

СРГ состоит из 48 антенн, расположенных Т-образно по направлениям запад—восток—юг с шагом в 4.9 м. Для построения изображений используются так называемые видности — комплексные кросскорреляции сигналов пар антенн, в которых одна из антенн принадлежит линейке запад—восток, а другая — линейке юг:

V ij ( v , t ) = gg , ( v , t ) g * ( v , t ) V j ( v , t ^ ,              ⁽¹⁾

где V_i j — искомая видность; g_i, g j — коэффициенты передачи антенн линеек восток — запад и юг соответ-

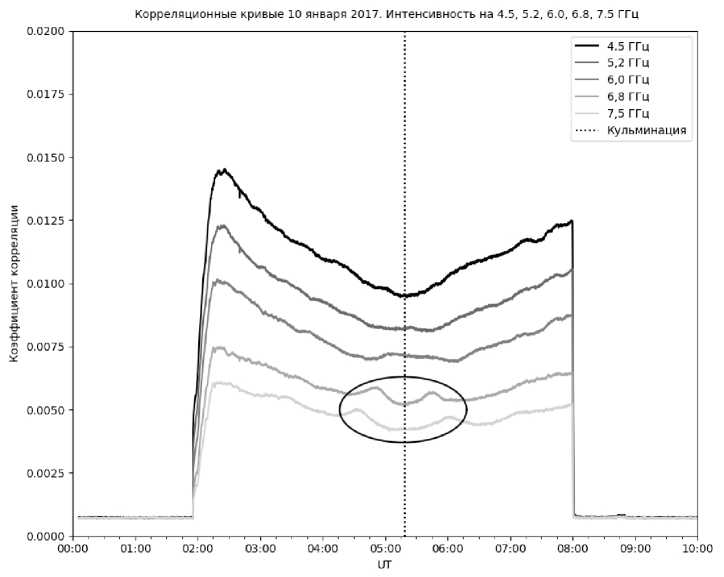
Рис. 1. Вариации корреляционных кривых, вызванные изменением диаграммы направленности СРГ. Овалом выделены вариации, которые можно принять за колебания плотности потока микроволнового излучения. Хорошо виден суточный ход кривых

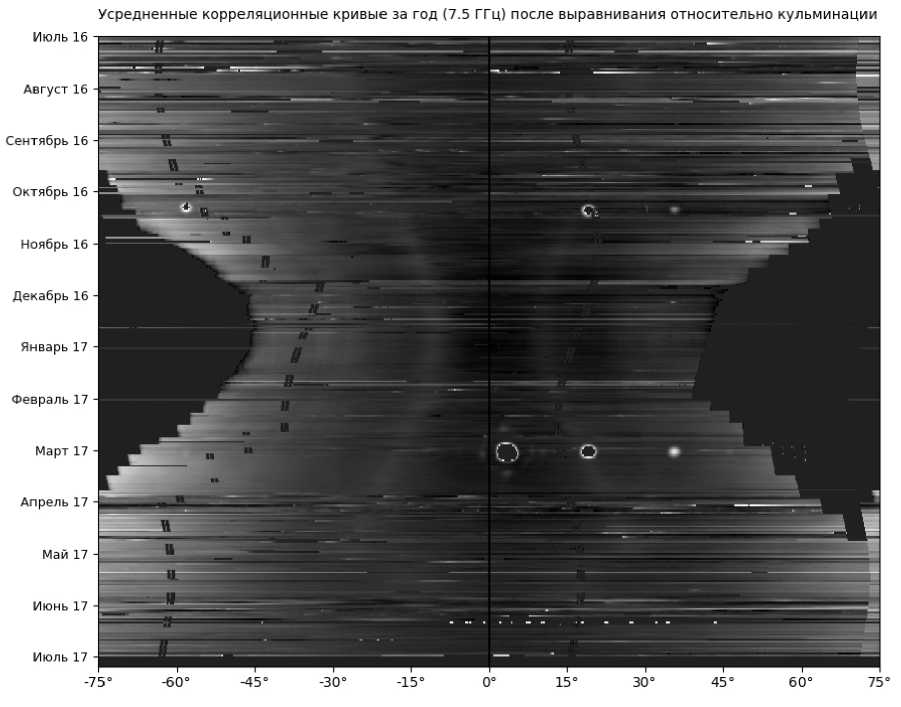
Рис. 2 . Корреляционные кривые, полученные с июля 2016 г. по июль 2017 г. По оси X отложен часовой угол, момент кульминации отмечен тонкой сплошной линией. Штриховые черные линии — моменты диагностики СРГ. Светлые дуги, симметрично расположенные относительно кульминации, — вариации корреляционных кривых. Обведенные белым кружки, относящиеся к датам наблюдений, близким к моментам равноденствия, — отклики на излучение геостационарных спутников

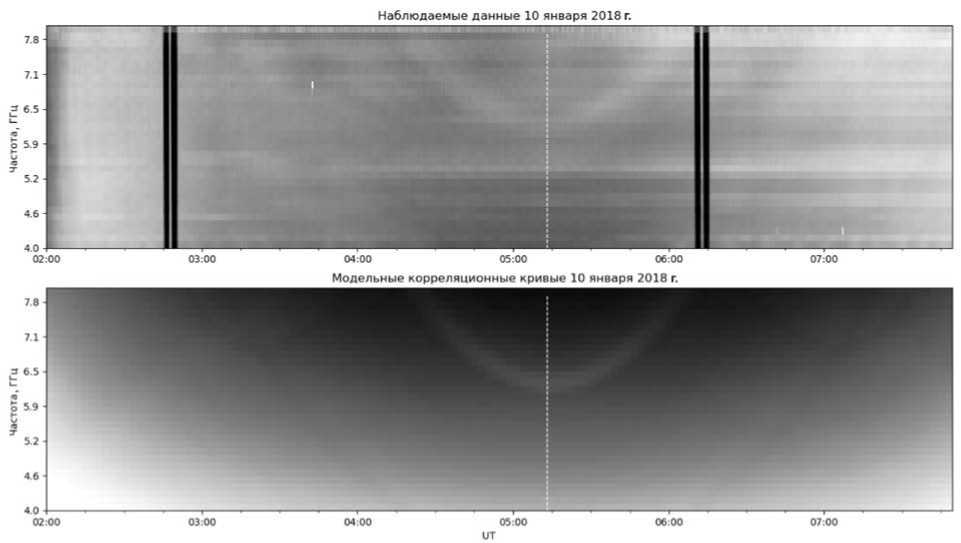
Рис. 3. Корреляционные кривые, полученные на 32 частотах в диапазоне 4–8 ГГц 10 января 2018 г. (верхняя панель): черные вертикальные полосы — моменты диагностики СРГ; белая пунктирная прямая — момент кульминации; вариации корреляционных кривых особенно хорошо заметны на интервале времени 04–06 ч в области высоких частот. Модельные корреляционные кривые (нижняя панель), рассчитанные в полной полосе частот СРГ 4–8 ГГц для 10 января 2018 г.

ственно; ν — частота; t — время; угловые скобки обозначают усреднение по времени. Каждой точке КК соответствует сумма модулей измеренных вид-ностей всех пар антенн в определенный момент времени на определенной частоте, т. е. сумма модулей комплексных коэффициентов корреляции сигналов каждой пары антенн i=32 j=16

C ( V , t ) = ££ | V ( v , t ),                      (2)

i = 1 j = 1

где i , j — индексы антенн направлений восток—запад и юг соответственно. Отклик одной пары антенн на распределение интенсивности по углам ξ, η можно записать в следующем виде [Томпсон и др., 2003] :

V ( V , t ) =

= jj F ( ^ , n ) cos(2 n ( u § + vn )) S fe П ) d ^ d П ,     ⁽³⁾

n где F(ξ, η) — диаграмма направленности одной антенны; S(ξ, η) — распределение интенсивности солнечного излучения; Ω — угловой размер источника излучения. Для нахождения отклика на солнечный диск примем, что распределение интенсивности излучения однородно на угловых размерах диска, а влиянием ДН одной антенны можно пренебречь. В этом случае выражение (2) будет иметь вид i=32 j=16      , ,

C ( v , t ) = EE M * j l - i = 1 j = 1

xjjn cos(2n( uj ^+uj n))d ^d n = i=32 j =16

=2 EE k-lkjh i=1 j=1

xj cos (2n ^ u2 + и 2 й^Пг ]4 -92d 9 = i=32 j=16

=n EE ЫЫ i = 1 j = 1

J 1 ( ^П V u ij ^{+ U} ij )

ⁿ V ^u 2 ^+U 2

где g_i , g j — коэффициенты передачи антенн i , j ; u_i j , υ ij — зависящие от ν , t компоненты пространственной частоты, J ₁ — функция Бесселя первого рода, Ω — угловой размер Солнца. Численное вычисление модельной КК с использованием выражения (4) не требует операций с двумерными массивами и поэтому выполняется гораздо быстрее, чем вычисление с использованием выражений (2), (3).

На рис. 3 показаны полученные на 32 частотах массивы реальных (вверху) и модельных (внизу) комплексных коэффициентов корреляции для 10 января 2018 г. Ясно видно, что во всем диапазоне частот выше 6 ГГц можно ожидать вариаций, подобных наблюдаемым вариациям КК на частотах 6.8 и 7.5 ГГц (рис. 1). Из модели КК для всей полосы частот следует, что эти изменения во времени вызваны меняющимся откликом СРГ на солнечный диск.

ВЛИЯНИЕ ВЗАИМНОГО ЗАТЕНЕНИЯ АНТЕНН НА КОРРЕЛЯЦИОННЫЕ КРИВЫЕ СРГ

СРГ предназначен для наблюдений Солнца. Этим определяется необходимое минимальное расстояние между антеннами, выраженное в длинах волн, — не больше величины, обратной угловому размеру Солнца. Если это требование не будет вы-

Моделирование отклика Сибирского радиогелиографа… полняться, то изображения будут накладываться друг на друга подобно тому, как накладываются спектры сигналов, дискретизация которых не удовлетворяет критерию Найквиста. В свою очередь, диаметры рефлекторов антенн солнечного радиоинтерферометра не могут быть слишком малы: это приведет к потере чувствительности. Поэтому для солнечных радиотелескопов возможны моменты, когда рефлектор одной антенны находится в тени рефлектора соседней антенны. Расположение антенн СРГ таково, что при отрицательных склонениях в определенные моменты времени антенна южного плеча, расположенная ближе всех к центру антенной решетки, затеняет ближайшие антенны восточного плеча при положительных часовых углах и западного — при отрицательных. Затенение не только уменьшает эффективную площадь соответствующего двухэлементного интерферометра, но и меняет его базу относительно расчетной, получаемой из проекции на картинную плоскость вектора, соединяющего фазовые центры антенн. Исключать затененные антенные базы нежелательно, потому что наибольшему затенению подвержены как раз минимальные базы, дающие наибольший вклад в отклик СРГ на солнечный диск. Ниже рассмотрим влияние затенения на корреляционные кривые СРГ.

Чтобы оценить изменение базы, вызванное затенением, рассмотрим рис. 4. Пусть без затенения база пары антенн определяется расстоянием O 1 O 2 . Если антенна A₁ начинает затенять A₂, фазовый центр A₂ будет смещаться по линии O 1 O 2 в сторону от антенны A 1 . Величину смещения можно найти из условия равенства площадей двух фигур из незатененной части A 2 , расположенных слева и справа от линии, проведенной через точку O₂ нормально к линии O₁O₂.

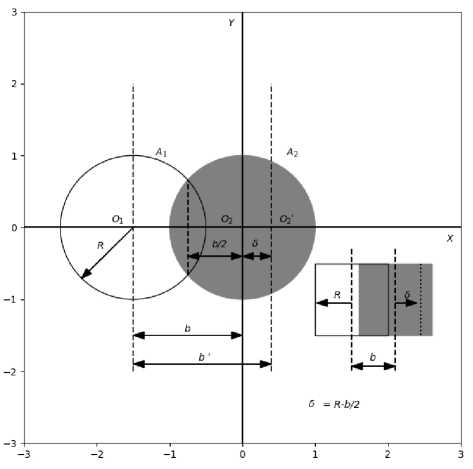
Рис. 4. Схематичное изображение затенения антенн. Расчетное расстояние между антеннами b — антенная база. Если антенна A₁ затеняет антенну A₂, то эффективная антенная база увеличивается: b' = b +δ, где δ — центр тяжести апертуры, не подвергшейся затенению. Для квадратной апертуры очевидно, что δ= R – b /2, где R — радиус зеркала. В первом приближении это выражение можно использовать и для круглых апертур

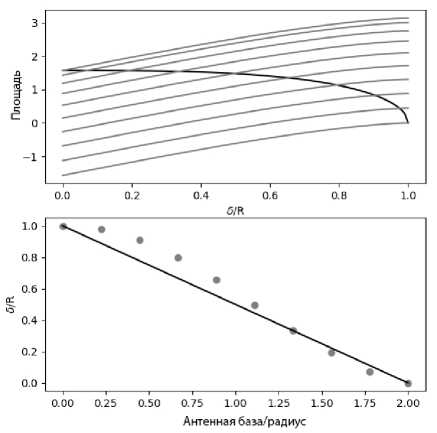
Рис. 5. Результат численного решения уравнения (7). Верхняя панель: черная кривая — S ₁(δ) и серые кривые — S ₂( b , δ). Искомые δ соответствуют абсциссам точек пересечения кривых. Нижняя панель: кружки — найденные значения δ, сплошная линия — зависимость δ( b ), полученная в предположении, что апертуры имеют форму квадрата. Видно, что в первом приближении вполне можно использовать выражение (8) для оценки изменения антенной базы из-за затенения

Площадь фигуры, расположенной справа,

R

5 1 ( 8 ) = 2 J 7 R ² - x ² dx,

где R — радиус зеркала антенны. Аналогично для площади левой фигуры имеем

5 ₂ ( b , 8 ) = 2 J 7 R ² - x ² dx - - R

• - b /2 ___________

• - 4 J 7 R ² - x ² dx .

  - R

Условие равенства S ₁= S ₂ приводит к выражению

8 ___________ - b /2 ___________

J 7 R ² - x ² dx = J 7 R ² - x ² dx ,                 (7)

0                   - R из которого можно найти связь δ и b, но выражение получается очень громоздким.

Результат численного решения уравнения S 1 = S 2 показан на рис. 5. Внизу показаны значения δ, полученные численно (кружки), и зависимость

δ= R – b /2,                                    (8)

полученная в предположении, что апертуры антенн A 1 , A 2 имеют форму квадрата и затенения происходят вдоль одной из его сторон (см. нижний правый угол рис. 4). Видно, что такое простое выражение вполне можно использовать для оценки того, как меняется антенная база из-за затенения одной антенны зеркалом другой антенны. При затенении отклик пары антенн с минимальной базой будет изменяться не только из-за уменьшения собирающей площади, но и вследствие эффективного увеличения длины базы. Это вызвано тем, что минимальная антенная база СРГ соответствует окрестности главного лепестка функции видности солнечного диска. Увели-

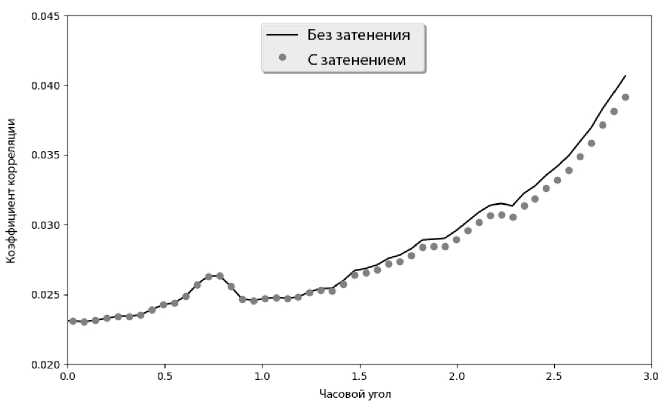
Рис. 6. Модели корреляционной кривой: сплошная линия — без учета затенения антенн; кружки — с учетом затенения (склонение –23°, частота 7.5 ГГц). В силу симметрии показана только половина корреляционной кривой, соответ-

ствующая положительным значениям часового угла

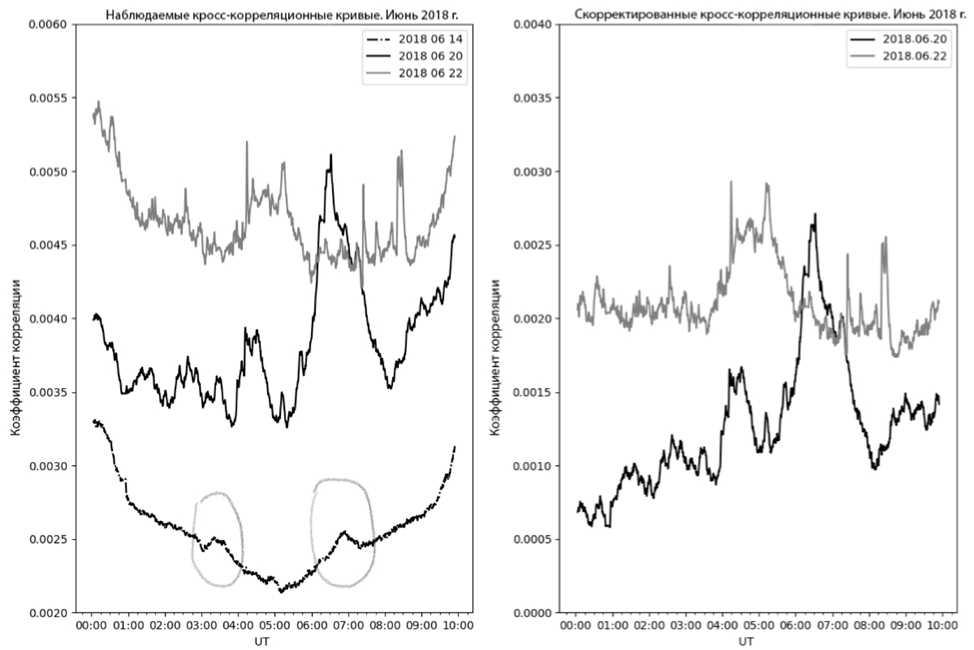
Рис. 7 . Корреляционные кривые 14, 20 и 22 июня 2018 (слева); 14 июня активность отсутствовала; 20 и 22 июня на диске появилась активная область NOAA12715. Овалами выделены вариации корреляционной кривой, вызванные откликом на солнечный диск. Результат вычитания корреляционной кривой за 8 июня из кривых за 20 и 22 июня (справа)

чение этой базы, другими словами — смещение спектральной чувствительности в область более высоких пространственных частот в окрестности главного лепестка функции видности, означает уменьшение отклика. Результат моделирования корреляционных кривых СРГ для момента зимнего солнцестояния показан на рис. 6. Видно, что существенное влияние затенение оказывает ко времени окончания наблюдений и его величина в пересчете на единицы плотности потока составляет не более 1 с.е.п. на частоте 7.5 ГГц.

КОРРЕКЦИЯ ОТКЛИКА СРГ НА СПОКОЙНОЕ СОЛНЦЕ

Хотя, как показывает рис. 3, модельные корреляционные кривые подобны реальным, все же ожидать абсолютно точного совпадения не приходится, поскольку реальная КК — это отклик не только на спокойный солнечный диск. Поэтому иногда для коррекции данной КК можно использовать реальную КК, полученную в момент отсутствия активных

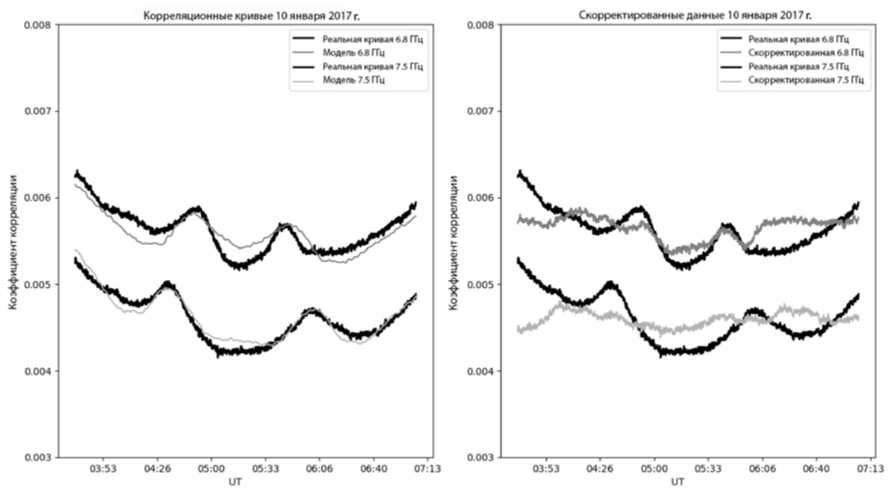
Рис. 8 . Результат коррекции корреляционных кривых с помощью модельных, рассчитанных как отклик на солнечный диск (частоты 6.8 и 7.5 ГГц): черные кривые — исходные, серые кривые — результат коррекции. Вариации КК удается уменьшить в несколько раз, до уровня плотности потока ~0.1 с.е.п.

областей на диске Солнца. На рис. 7 показан результат такой коррекции для КК, полученных 8–22 июня 2018 г. На диске Солнца 8 июня активных областей не было. Активная область NOAA 12713, присутствующая на диске 15 июня, не давала заметного вклада в КК, хотя слабые вспышки наблюдались. Значения коэффициентов корреляции заметно выросли 20 и 22 июня, при этом наблюдалось большое количество слабых всплесков, которые можно интерпретировать как шум активной области, соответствующий моменту всплытия ее из-под фотосферы. Результат коррекции данных за 8 июня показан в правой части рисунка. Хорошо видно, что такие корректированные данные более достоверно описывают изменения плотности потока излучения от активных областей, но вместе с тем на корректированные КК переходят артефакты корректирующей КК (они отмечены овалами). На практике такой метод вполне пригоден, если на приемлемом интервале времени отсутствовала активность от исследуемых событий. Приемлемость в данном случае — малое изменение отклика на спокойное Солнце. В остальных случаях нужно рассчитывать модельные КК.

С помощью вышеописанного метода были рассчитаны модельные КК, показанные на рис. 1. Коррекция проведена для КК, полученных на частотах 6.8 и 7.5 ГГц, где вариации наиболее выражены. Суточный ход модельных и реальных КК немного различается. Скорее всего, это вызвано тем, что все же в этот день присутствуют компактные источники, КК для которых слабо меняются в течение дня, поэтому ход суммарной кривой более плавный, чем модельный отклик на спокойный солнечный диск. Асимметрия КК относительно кульминации может быть вызвана асимметрией распределения интенсивности по диску Солнца или различием в коэффициентах передачи антенн, симметрично расположенных относительно центра антенной решетки СРГ.

Наиболее однозначная информация о коэффициентах передачи антенн — это результаты диагностики СРГ, проводимой дважды в день. Диагностика заключается в том, что все антенны СРГ отводятся от направления на Солнце по часовому углу на некоторое время. Это позволяет измерить разницу между откликами на небо и Солнце для каждой антенны в полной полосе частот. Эта разница пропорциональна модулю коэффициента передачи антенны. Чтобы учесть оставшееся отличие в суточном ходе КК, достаточно использовать квадратичную зависимость от часового угла вида c ( h )=1–( h – h 0 )², где h 0 — смещение параболы, для того чтобы внести необходимую асимметрию в отклик. Результат коррекции показан на рис. 8. Вариации корреляционных кривых удается уменьшить в несколько раз, до уровня плотности потока излучения примерно 0.1 с.е.п.

ЗАКЛЮЧЕНИЕ

Предложенный метод моделирования корреляционных кривых СРГ описывает наблюдаемые особенности КК, обусловленные откликом СРГ на солнечный диск, и, соответственно, позволяет корректировать КК или учитывать их вариации при обработке данных СРГ. Рассмотрены два фактора, влияющие на вариации КК в течение дня: изменение ДН СРГ, ведущее к различным проявлениям функции видности солнечного диска на КК, и влияние взаимного затенения антенн на длины антенных баз и собирающие площади. Показано, что оба этих фактора сильнее всего проявляются при отрицательных солнечных склонениях и вариации КК на высоких частотах могут достигать 0.1 %, что соответствует плотности потока излучения 1 с.е.п. Наилучшее совпадение модельных КК с реальными получается в предположении, что край диска Солнца размыт. Представляется интересным сместить акцент работы по моделированию КК на то, как зависят от частоты диа- метр солнечного диска и степень размытости края диска. Что касается затенения антенн, то, судя по всему, его влияние должно больше проявиться при построении изображений, а не корреляционных кривых. Поэтому интерес представляли бы работы по моделированию ДН СРГ с учетом взаимного затенения антенн.

Работы по разделу «Влияние взаимного затенения антенн на корреляционные кривые СРГ» выполнены за счет средств Российского научного фонда (проект № 18-12-00172), по остальным разделам — в рамках государственного задания на 2018 г. № 007-00163-18-00 от 12.01.2018.