Моделирование отражения электромагнитных волн от дифракционных решёток, нанесённых на произвольную поверхность

В современной науке и технике часто используют приборы, работающие по принципам дифракционной оптики [1, 2].

Многие из них содержат в своей конструкции дифракционный оптический элемент (ДОЭ). Эти элементы представляют собой совокупность большого числа регулярно расположенных щелей или выступов, нанесённых на некоторую поверхность, то есть являются дифракционными решётками [3]. Эти решётки можно разделить по свойствам поверхности на три типа: плоские [3], сферические [1] и решётки, выполненные на более сложных поверхностях свободной формы. В настоящее время отсутствует методика численного исследования работы дифракционной решётки, выполненной на произвольной поверхности. Для решения задач дифракции используется метод, в основе которого лежит интегральная теорема Кирхгофа [4], согласно которой значение функции и , являющейся решением скалярного уравнения Гельмгольца, в произвольной точке М ( х , у , z ), находящейся внутри замкнутого объема, выражается через значение функции и и ее первой производной на поверхности, ограничивающей данный объем [4]. Метод Кирхгофа является математическим обобщением принципа Гюйгенса–Френеля, основная идея которого состоит в том, что волновое возмущение в некоторой точке пространства М есть результат интерференции волн, испускаемых вторичными источниками [4]

Метод Кирхгофа позволяет получить математические описание распространения света с учетом дифракции. Геометрооптический подход не позволяет получить точного объяснения поведения системы в случае дифракционно-ограниченной оптической схемы.

Устройства, использующие дифракционные зеркальные решётки, выполненные на сферических поверхностях, рассмотрены в работе [5]. Во многих работах уделено большое внимание дифракционным решеткам на плоской поверхности и мало уде-

2-194-202.

ляется внимания решёткам, нанесённым на более сложные поверхности. Данная работа посвящена описанию процесса отражения светового поля от поверхности, на которую нанесен ДОЭ. Использование для решения метода Кирхгофа позволяет определить более точное распределение светового поля на выходе системы, чем в случае геометрической оптики.

Суть подхода, рассмотренного в данной работе, состоит в том, что волновое поле (в общем случае с негладким волновым фронтом) в области ДОЭ, нанесенного на криволинейную поверхность, представляется в виде суперпозиции полей с гладкими волновыми фронтами. Это позволяет применить для расчета соответствующих интегралов асимптотические методы, например, метод стационарной фазы или метод трассировки лучей [6]. В результате получается метод, который содержит преимущества как дифракционного, так и геометрооптического подходов. Это облегчает вычислительную сложность задачи по сравнению с непосредственным применением метода Кирхгофа (а тем более по сравнению с методами, основанными на разностной аппроксимации дифференциальных уравнений) на порядок.

В качестве проверки теоретических результатов была рассмотрена дифракция на решетке, нанесенной на сферическую поверхность. В рамках параксиального приближения были получены аналитические формулы для распределения энергии в области фокусировки. Сравнение результатов с известными подтвердило правильность рассмотренного в работе подхода и модификации метода Кирхгофа.

• 1.    Интеграл Кирхгофа в случае задания начального распределения на криволинейной поверхности

  • 1.1.    Постановка задачи

В рамках скалярной теории волновое поле удовлетворяет уравнению Гельмгольца:

d ² U ^U ^U      „

—г+—г++ k 2 и = 0, о x    о у    о z

где координаты x , y , z – декартовы координаты в трёхмерном пространстве.

Пусть на поверхности, заданной в параметрическом виде r = r ( u, v ), задана комплексная амплитуда:

U ( u , v ) = A ( u , v ) exp ( ik ^ ( u , v ) ) ,

амплитуда поля задана на криволинейной поверхности. Выражение для нормальной производной имеет вид:

V1G (k - rJ) = ik expГik|r- rJ)|r- rJ-expГik|r- rJ) r- r    (7)

r - r                     ^{- r}J'

где A ( u , v ) = I l ( u , v ) , I ( u, v ) - интенсивность, k =2 л / % -волновое число и Т ( u, v ) - функция эйконала на рассматриваемой поверхности.

Требуется найти решение уравнения Гельмгольца в окружающем поверхность пространстве.

1.2. Интегральное представление решения

Интегральное представление для решения уравнения Гельмгольца с использованием теоремы Грина имеет следующий вид:

U ( г ) =

= Т"^ ( ^Г G ( r - r ¹ ) ^V U ( r ¹ ) ^- U ( r ¹ ) ^{V 1} G ( r - r ¹ )¹ i ^{d 5 1} ) .( ) 4 n

Подставляя (7) в (2) и пренебрегая членами, содержащими ( k | r – r 1 |)^–1, получаем следующее выражение для поля

U ( r ) =

ГГ                 ^)

= 4^ I V IP: r ) + r r IU(r1)G(r-r1 )• dS1 4П v<                   ii уу

Для поверхности, заданной в параметрическом виде, векторный элемент площади на поверхности имеет вид dS = N (u, v) du dv = [ru (u, v )x rv (u, v)] du dv . (9)

Здесь r – радиус-вектор точки наблюдения, r 1 – радиус-вектор точки на поверхности, dS 1 – вектор, который по модулю равен элементу площади поверхности, по которой ведётся интегрирование, а по направлению совпадает с вектором нормали. Точка обозначает скалярное приближение ( • ).

В качестве функции Грина будем использовать функцию

Здесь N ( u , v ) – нормаль к рассматриваемой поверхности, r u ( u , v ) и r v ( u , v ) – производные радиус-вектора поверхности по координатам. [×] – обозначе-

но векторное произведение векторов.

Выражение для поля принимает вид

+

^{r r - r} ( ^u , ^v ) ^ |r - r ( u , v )|

, N ( u , v ) x

у

у

+

^G ( ^{r -} r 1 ) =

exp Г ik |r - r ^

Ir - rJ

x U ( u , v ) G (| r - r ( u , v )|) d u d v ,

Из формулы (2) следует, что для нахождения поля внутри объема необходимо знать на поверхности поле U ( r 1 ) и градиент ( V 1 U ( r 1 )).

Рассмотрим выражение для градиента. Функция U ( r 1 ) представляется в виде

p ( u , v ) = V ₁ Y ( r ₁ ) .

Функция p ( u , v ) находится из системы уравнений

U ( r ) = A ( r ) exp ( ik ^ ( r x ) ] .

Здесь A ( r ) = 1 1 ( r ) , где I (п) - интенсивность

волны на поверхности, k - это волновое число и ^ ( r | ) – это функция эйконала на рассматриваемой поверхности.

В приближении геометрической оптики

3T ( u , v ) Г / \ d r ( u , v ) )

——=| р ( ^u , ^v ) ,—— I, d u     ^          d u у

ЭТ( u , v) Г         dr ( u , v ))

-^(-^-2 = I p ( u , v ), -(-^-2 I,                  (12)

d v     ^          d v у

( p ( ^u , ^v ) ) ² = 1.

Система уравнений (12) имеет аналитическое решение для любой поверхности, заданной в параметрическом виде.

V U ( r ) = ik ( V^ r )) U ( r ) .                       (5)

Подставляя выражение (5) в (2), получаем выражение для поля в виде

2. ДОЭ на криволинейной поверхности

Пусть на поверхности, заданной в параметрическом виде r = r ( u , v ), задана комплексная амплитуда

U (r ) = 1-1U (r1 )x

4n x ГikG (r - r1 ) V^ (r1) - V1G (r - r1)у dS1.

U ( u , v ) = A ( u , v ) exp ( ik T ( u , v ) ) ,

Формула (6) представляет собой решение уравнения Гельмгольца при условии, что комплексная

где A ( u , v ) = I l ( u , v ) , I ( u , v ) I ( u , v ) - интенсивность, k =2лА - волновое число, и Т ( u , v ) - функция эйконала на рассматриваемой поверхности. Пусть на кри-

волинейной поверхности находится ДОЭ с высотой микрорельефа, описываемой функцией h (u, v) = (h / 2п)ф(mod2l (kdфd (u, v))),        (13)

где ф d ( u , v ) — функция эйконала ДОЭ, % - длина волны освещающего света, ф d ( u , v ) - функция эйконала оптического элемента, Ф( x ) – функция нелинейного предыскажения. Функция Ф( x ) – описывает технологические погрешности или эффекты квантования ДОЭ. Физический смысл эйкональной функции состоит в следующем: k d ф d ( u , v ) представляет собой фазу световой волны в плоскости, непосредственно прилегающей к ДОЭ.

В качестве примера рассмотрим оптический элемент с функцией эйконала фd(u, v) = au. В этом случае высота микрорельефа описывается выражением h (u ) = (h0/2n)mod2n( kd au). (14)

ДОЭ представляет собой дифракционную решётку с треугольным профилем и с периодом d = 2 п / k a .

Пусть на дифракционную решетку, расположенную в плоскости z =0, падает плоская волна с эйконалом ф ₀ ( u , v ) = s ⁰ i r , где s ⁰ - вектор направляющего луча, а r – вектор с координатами r = ( u , v , 0). После прохождения дифракционной решетки на выходе образуются несколько плоских волн с направляющими векторами

s

m

s ^{0 +} m

^дф d ( ^u , ^v ) d u

s " ,

)

⁽ s m ) z

J

Компонента ( s m ) z находится из условия нормировки вектора | s m | = 1.

Рассмотрим оптический элемент с эйкональной функцией

ф d ( u , v ) = a u + P v .

Этот ДОЭ представляет дифракционную решетку со штрихами, направленными не по оси u . Вектор b , определяющий направление, перпендикулярное направлению штрихов, и период дифракционной решетки d выражаются через параметры a , в по следующим формулам:

,       2п d = —, k a2 + в2

b = У_±ф ( u , v ) .

На выходе дифракционной решетки образуются множество плоских волн с направляющими векторами

s

m

s ⁰ + m x

^дф d ( ^u , ^v ) d u

s y + m

NAuvv) d v

( S m ) z ] . (18)

Компонента ( s m ) z находится из условия нормировки вектора | s m | = 1.

При прохождении плоской волны через дифракционную решетку образуется несколько плоских волн. Эйконал каждой волны получается как результат сложения эйконала падающей волны - ф о ( u , v ) и эйконала ДОЭ - ф d ( u , v ), умноженного на номер ди-

фракционного порядка. Эйконал ДОЭ для порядка m имеет вид:

ф m ( ^u , ^v ) = ф о ( ^u , ^v ) ^{+ m} ф d ( ^u , ^v ) .                    ⁽¹⁹⁾

Рассмотрим теперь падение волны с эйконалом ф 0 ( u , v ), отличным от эйконала плоской волны. Направление вектора луча определяется

s ⁰

дф ₀ ( u , v ) дф ⁰ ( u , v )

д u

<

,

d v

^

, ( s 0 }

^ ^{J z}

J

.

Компонента ( s ⁰) z находится из условия нормировки вектора | s ⁰| = 1.

Теперь дифракционная решетка локально изменяет направление луча. В этом случае направление луча на выходе также описывается формулой (19)

s _m

дф ₀ ( u , v ) дф d ( u , v ) --+ m--------

d u

d u

,

дф ₀ ( u , v )      дф d ( u , v )

--+ m--------

d v

d v

’ ⁽ s m ) z I .

Рассмотрим теперь более общий случай. Пусть волна с эйконалом ф о ( u , v ), отличным от эйконала плоской волны, падает на ДОЭ с эйкональной функцией, отличной от эйконала дифракционной решетки. В этом случае дифракционный оптический элемент представляет собой дифракционную решетку с изменяющимся по апертуре периодом и направлением штрихов. Сделаем предположение, что изменение направления луча определяется только периодом локальной решетки и направлением штрихов локальной решетки. Отметить, что период решетки и направление штрихов определяются формулами

d ( u , v ) =

2 n

k d |^ф d ( ^u , ^v )Г

b ( u , v ) = Уф d ( u , v ) .

Направление также определяется формулой (21). Рассмотрим теперь самый общий случай. Пусть волна с эйконалом ф 0 ( u , v ), отличным от эйконала плоской волны, падает на ДОЭ с эйкональ-ной функцией, отличной от эйконала дифракционной решетки. Положим, длина волны освещающего

пучка отлична от длины волны, которая использовалась при расчете микрорельефа по формуле (13). Направление лучей после прохождения ДОЭ опре-

деляется выражением:

^S m = ⁽Т"( ф m ( u , v ) )’Т"( ф m ( u , v ) ) , ( s m )_z ^ ,       ⁽²³⁾

V д u             д v                  ^z J

⁽ s m ) z =A ¹

a u ^(ф - ^{( u} • v

Л( ф m ( ^u , ^v д v

ф m ( u , v ) = ф 0 ( u , v ) ⁺ mk d- ф d ( u , v ) . k ₀

Анализ полученных выражений показывает, что после прохождения ДОЭ на выходе формируется несколько семейств лучей, притом каждому семейству соответствует свой порядок дифракции с номером m .

Формулы (23), (24) получены для ДОЭ, расположенного на плоскости.

При расположении ДОЭ на криволинейной поверхности формула (24) остаётся справедливой, а направление каждого из семейств лучей определяется выражением:

^дФ m ( u , v ) ( / X ^d r ( u , v ) )

-------- = 1 P ⁽ u , v ) ,^I,

• d u      ^ d u J

• ^дФ m ( u , v ) f , X ^d r ( u , v ) )                     z₀,x

  -----3 = I P ( u ’ v ) , з I’                       ⁽²⁵⁾ d v      ^ d v J

( p ( ^u , ^v ) ) ² = 1.

dT ( u , v ) =      - x ₀

^{d u}        R ² - 2 uX o + x 02

dZ ( u i v ) = ₀ d v

3. Интеграл Кирхгофа для ДОЭ на криволинейной поверхности

Подставляя выражения (25) и (26) в (12), получаем систему уравнений для нахождения p ( u , v ).

- x₀              , x    P 3 ( ^u , ^v ) ^u

,                = p , ( u , v ) —,          =,

R ² - 2 ux ₀ + x 02             V R - u ² - v²

, .       Px (u, v) v k = p 2 (u,v)- -7=L=L=,                (29)

V R - u ² - v²

P 1 ( u , v ) + p 2 ( u , v ) +

+ p 3 ( u , v ) ² = 1.

При рассмотрения ДОЭ на криволинейной поверхности рассуждения будут такими же, как в 1-м параграфе, с той лишь разницей, что интеграл Кирхгофа будет записан с использованием новой эй-кональной функции вида (24), где ф о ( u , v ) - эйкональ-ная функция самой поверхности, а ( mk d / к о ) ф d ( u , v ) -эйконал дифракционного порядка с номером m ДОЭ. В этом случае в интеграле (10) необходимо переопределить функцию U ( u , v ) следующим образом:

exp| ik\ ф0 (u,v) +     '"фd (u,v) I I и (u • v ) =       -----т4-------^■   (26)

Фо ( ^u , ^v )

Ввиду изменения вида эйкональной функции будут внесены соответствующие изменения в систему, определяющую вектор направления.

4. Расчёт поля сферической волны, отражённой от сферического зеркала

В случае, когда поверхность сферическая:

x = x (u, v) = u, y = y (u, v ) = v, z (u, v) = V R - v2 - u2,

Переходим к интегрированию по параметрам и получаем выражение, описывающее отражённое световое поле (см. приложение Б).

Выражение (11) определяет собой вектор направления лучей при их движении через рассматриваемую оптическую систему.

В случае сферической зеркальной поверхности легко перейти от последней системы к квадратному уравнению, выразив из первых двух уравнений системы (29) p 1 и p 2 через p 3 , а затем подставив в третье уравнение системы. Результатом будут два вектора, определяющих направление отражения волны от рассматриваемой поверхности, однако правильный физический смысл будет иметь только один, который будет получаться из того решения квадратного уравнения, которое меньше нуля.

Моделирование заключалось в численном расчёте интеграла Кирхгофа и дальнейшем его сравнении с параксиальным приближением.

Для моделирования с помощью интеграла Кирхгофа были использованы следующие формулы.

Точка наблюдения:

r = ( x , y , z ) .

N =

R ²

V R² - u ² - v ²

; 1

Точка на поверхности сферического зеркала: r ( u , v ) = f u , v , V R - u ² - v ² J ,                       (30)

r - r ( u , v ) = ^f x - u ; y - v ; z - V R ² - u ² - v ² I .      (31)

dr (u,v) = f10     - u du     I ’ ’ V R - u2 - v2

d r ( u , v ) d v

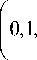
R

Далее будем считать, что z = 0. Расстояние от точки на поверхности до точки наблюдения определяет-

ся выражением:

- v

u ²

|r - r ( u , v )| = ( x - u ) 2 + ( v - y ) ² + f R ² - u ² - v ² ^] . (32)

При расположении точечного источника в точке с координатами ( x 0 ,0,0) освещается сферическая поверхность. Функция эйконала в этом случае примет вид T ( u , v ) = -JR ² - 2 ux ₀ + x 0 .

Производные эйкональной функции описываются выражениями:

Функция Грина:

,,/1      , x|A ^exP^{( ik} |^{r - r} ( ^u , ^v )|)

G ( ^{r - r} ( ^u , ^v ) ) = i , .

| r - r ( u , v )

Функция, описывающая поле от точечного источника на сферической поверхности, имеет вид:

exp ( ik ^ ( u , v ) )

U ( u , v ) =---------------- ^v ’       ^ ( u , v )

.

Подставляем p ( u , v ), а также выражения (32), (31) в формулу (10), получаем выражение для поля в плоскости ( x, y ) (см. приложение А).

В параксиальном приближении выражение для поля сферической волны, отражённой от сферическо-

го зеркала, имеет вид:

2 ikab _2M ikk

U (x, у ) =--e-kR kRe2 Re 2 R nR2

. Г a ( x + x 0 ) I . Г by I x sinc k -------- sinc k ,

I R JI R J

где x 0 – положение на оси абсцисс источника, a , b – размеры исследуемой области по оси абсцисс и ординат соответственно.

Подробный вывод аналитики смотри в приложении Б.

Моделирование проводилось для зеркальной дифракционной решётки, выполненной на сферической поверхности радиусом 30 % . График амплитуды для

5. Расчёт поля сферической волны, отражённой от сферического зеркала с дифракционной решёткой

Для описания отражения от сферической дифракционной решётки достаточно изменить выше описанную функцию источника (34), добавив в аргумент экспоненты функцию, определяющую характер поверхности дифракционной решётки.

exp ( ik ф о⁽ u , v ) )

U ( u , v )=        —--- .                      ⁽³⁶⁾

Ф о ( u , v )

Новой функцией источника будет формула (26). Запишем ее в более компактном виде:

exp ( ^ik Ф о^{( u} , ^v ) ⁺ m Ф ^{( u} ) )

^U ( u , v ) =----------;—;------- ,              ⁽³⁷⁾

Ф о ( u , v )

где m – исследуемый дифракционный порядок.

Здесь добавленная в аргумент функция имеет вид:

Ф ( u ) = ( A x / R ) x u ,                              (38)

где A x и R - шаг и радиус поверхности решётки соот-

ветственно.

этой системы, отражающей свет длиной волны

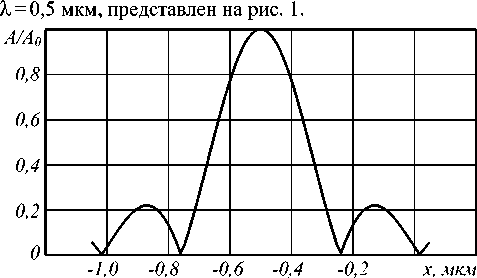
Рис. 1. График амплитуды в плоскости y = 0 в случае численного решения

Методика численного моделирования практически не отличается от описанной в предыдущем параграфе за исключением новой функции, описывающей источник (37). Так же изменится и аналитическое решение (35), которое теперь примет следующей вид:

U (x, у)

x sinc I k

2 ikab

nR2

exp I ikR

x ²

2 + —°y + 2 R ²

2      2 A \ x2 + у2 || x 2R2 J

a ( x + x ₀ -

R

m д xR )

• G by I sinc k .

I R J

На следующем рисунке представлен график ам- плитуды рассматриваемой системы, но описанной

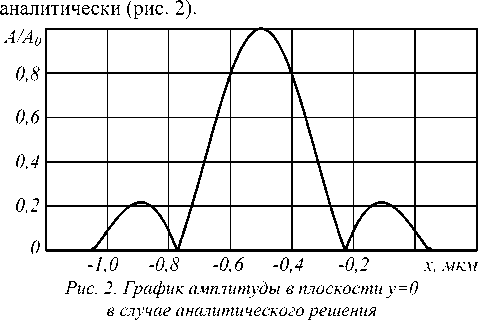
Для моделирования работы дифракционной решётки был проведён расчёт трёх порядков дифракции, а именно –1, 0, 1, для различных расстояний и наборов длин волн. На рис. 3 а представлено численное решение для нулевого порядка дифракции, на рис. 3 б – для того же порядка, но для аналитики. Для рис. 3 г , е – численное решение, соответственно, первый и минус первый порядки дифракции. Для рис. 3 в , д – аналитическое решение, соответственно, первый и минус первый порядки дифракции.

Сравнение результатов для аналитического и численного решений представлено на рис. 4, где сплош-

ная линия соответствует численному решению, а пунктирная – аналитическому.

Заключение

В процессе численного моделирования результаты показали, что при удалении источника от зеркала оба решения приближаются друг к другу.

Разработанный метод может быть использован при расчете характеристик оптических схем, содержащих ДОЭ на криволинейной поверхности. Данный подход может быть обобщен на случай векторного электромагнитного поля. Описанный математический аппарат позволяет моделировать отражение от дифракционных решёток, нанесённых на произвольную поверхность. Для решения поставленной задачи использован аналог метода Кирхгофа. В качестве примера было рассмотрено отражение от дифракционной решётки сферической поверхности.

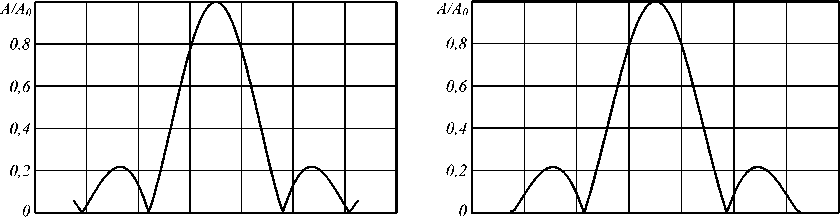
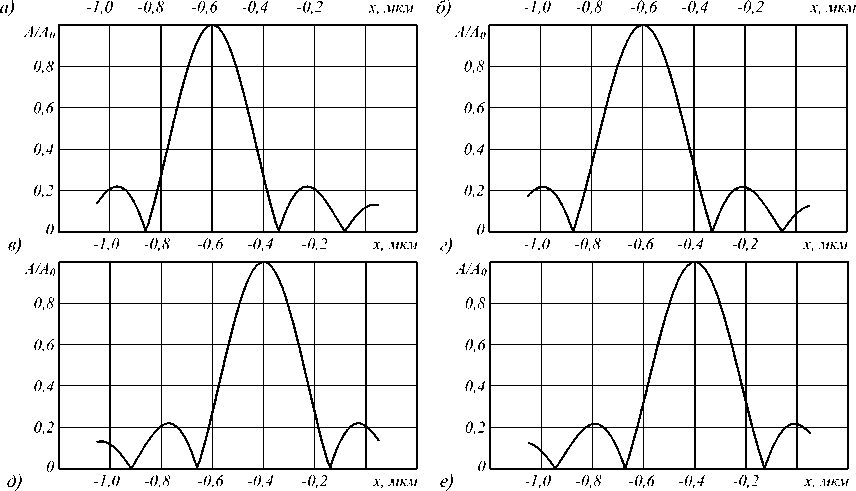
Рис. 3. График амплитуды в плоскости y = 0 для –1, 0,1 порядков дифракции для численного и аналитического методов решения

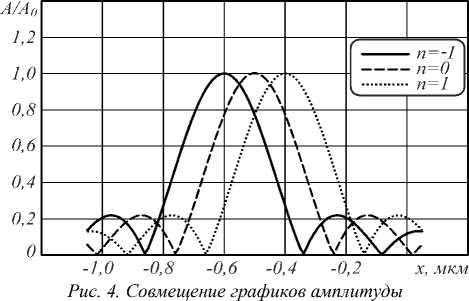
в плоскости y = 0 для -1, 0,1 порядков дифракции для численного и аналитического методов решения

Для моделирования таких систем была разработана программа и проведено численное исследование. Рассмотрена возможность обобщения полученных результатов для произвольных дифракционных оптических элементов.

Приложение A. Решение системы уравнений для поиска направляющего вектора

Направляющий вектор p ( u , v ) легко найти из системы уравнений:

<

u - x

Ir - r (u, v )|

v - y

Ir - r (u, v )|

= A (u, v)-

p 3 ( u , v ) u 4 R - u ² - v²

= P 2 ( u, v )-

P 3 ( u , v ) v V R - u ² - v²

P 1 ( u , v ) ² + p 2 ( u , v ) ² + p 3 ( u , v ) ² = 1.

(А.1)

Для компактности решения введём обозначения:

u - X о

Ir - r (u, v )|

b = ^{v -} y 0 , I r - r ( u , v )|

c =

u

V R - u ² - v²

, d =

v

V R - u ² - v²

(А.2):

Теперь перезапишем систему (A.1)

a = pi (u,v) + cp3 (u,v) ,

< b = p 2 ( u , v ) + dp 3 ( u , v ) , _ p i ( u , v ) 2 + p 2 ( u , v ) 2 + p 3 ( u , v ) 2 = 1.

(А.2) с помощью

(А.3)

Выражать будем p 1 и p 2 из первых двух уравнений системы (A.3), чтобы при подстановке их в третье уравнение той же системы получить квадратное уравнение:

a - cp3 (u, v ) = Pi (u, v), b - dp 3 (u, v ) = p 2 (u, v),

( a - cp 3 ( u , v ) ) 2 + ( b - dp 3 ( u , v ) ) 2 +

+ p 3 ( u , v ) 2 = 1,

( a - cp 3 ( u , v ) ) 2 + ( b - dp 3 ( u , v ) ) 2 +

+ p 3 (u, v )2 = 1, a2 - 2 acp3 (u, v) + (cp3 (u, v)) + b2 -

- 2 bdp 3 ( u , v ) + ( dp 3 ( u , v ) ) 2 + p 3 ( u , v ) = 1.

|r - r ( u , v )| = R .

(Б.3)

(А.4)

(А.5)

(А.6)

Учитывая формулы (Б.2, Б.3) и подставляя их в систему уравнений (A.1), определяющую направляющий вектор p , получим:

u - X / x

= p 1^{( u} ’ ^{v )}

R

p 3 ( u , v ) u

V R - u²

v ²

<

v - y , .     p 3 ( ^u , ^v ) ^v

= p 2 ( ^u , ^v ) ^-          2    2 ,

^R             R - - u ²- v²

p 1 ( u , v ) 2 + p 2 ( u , v ) 2 + p 3 ( u , v ) ² = 1.

(Б.4)

После всех преобразований (A.5, A.6) получаем уравнение (A.7), в котором опять же целесообразно сделать замену для его более компактной записи.

p з ( u , v ) ^ 1 + d + c 7 —

- 2 p 3 ( u , v )( ac + bd ) + ( a ² + b ² - 1 ) = 0.

Введём новые обозначения:

A = ^ 1 + d ² + c ² 7 ; B = - 2 ( ac + bd ) ;

C = ( a ² + b ² - 1 ) .

Далее принципиальных отличий от решения этой системы, описанного в приложении А, нет. Поэтому сразу запишем ее решение (Б.5) в случае очень большого R :

Решение уравнения (A.7) получим в виде:

p 3 , 1 =

- B + Bb ² - 4 AC

2 A

p 3 , 2

- B - Bb ² - 4 AC

2 A

(А.7)

(А.8)

(А.9)

Значения этих корней легко получить, подставив в А.9 обозначения (A.8).

Распространение луча от источника происходит в положительном направлении, значит, отражённый луч будет двигаться в отрицательном направлении, а значит, нужно брать p 3 со знаком минус.

Приложение Б. Получение параксиального приближения для зеркальной поверхности

Значение интеграла

+

+

r - r ( u , v )      ,

I—/—d, ^{N ( u} , ^{v )}

V |r - r ( u , v )|           J

x

(Б.1)

x U ( u , v ) G ( |r - r ( u , v ) ) d u d v

может быть получено в параксиальном приближении. Для получения параксиального приближения предполагаем, что радиус поверхности достаточно большой.

В этом случае для выражения | r – r ( u , v )| возможно

следующее:

| r - r ( u , v )| = R I 1 +--------

- 2 ux - 2 vy

2 R ²

(Б.2)

Формула (Б.1) справедлива в том случае, когда | r - r ( u , v ) | является аргументом экспоненты.

Иначе имеем:

p = 0 ; p 2 = 0 ; p 3 = ± 1.

(Б.5)

Нормаль в случае параксиального приближения запишется в следующем виде:

N = 1 I---—

V V R ² - u²

v ² R ²

^= ; 1 I = ( 0 ; 0 ; 1 ) . (Б.5) - u ² - v ²    7

Разность векторов: r - r ( u , v ) = ( 0 ; 0 ; R ) .

(Б.6)

Подставляя (Б.6, Б.5) в скалярные произведения, входящие в формулу Б.1:

r - r (u, v).

I---- ;—j , ^{N ( u} , ^{v )} =

V |r - r (u, v)|^I

((0;0;R) ,,)

H ¹"!^ 0 ; 0 ; 1) I = 1,

R

( p ( u , v ) , N ( u , v

(Б.7)

(Б.8)

Подставляя (Б.7, Б.8) в формулу Б.1, получаем:

A ik          /xp ⁽ ik l^r- r ⁽ u , v ⁾ )

U ( r ) = — J U ( u , v )--- 1----j—^L d u d v =

2 n                r - r ( u , v )

2 n R

2      2

+ X ² + y ²

1 + x

2 ux ₀

< v -

2 ux - 2 vy

2 R ²

2 R ²

+

f_i X ²

Внутри экспоненты: ф 0 ( u , v ) = R I 1 + —°

Вне экспоненты: ф ₀( u , v ) = R , kx 0 ^ik ( ^x у 2 ) ik    2 ikR

U ( r ) =----- ee e ² R e ² R x

2 n R ²

x J exp I - ik

u ( ^x + ^x 0 ) + vy ) ----------------I d u d v .

R

- 2 ux ₀

2 R ²

.

Пусть ik Const =---- e

2 n R ²

ikx 2    ^ik ( ^x 2 + У 2 )

2 ikR e 2 R 0 e   2 R   ,

Я Г    u ( x + x ₀ )

exp - ik--------

D V R uv

2 f      u (x + x 0) | 2

d u d v = Const exp - ik ------- d u

R

• u ,         V                     7      v ,

  / пусть пределы будут симметричными /

Const R ²

k ² y ( x + x ₀ )

exp

V

- ik

a (x + x 0)1      f - a (x + x 0 ) Y

___ I — exp I — ik------- I

У V               УУ

-

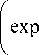
ikb 1

R У

exp

- ik - by

R

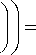
(Б.9)

ConstR2 f      f  , a(x + x0) 1      f , a(x + x0)Yf      f  , by 1      f , by 11

—:—;------ - exp -ik------- + exp ik------- - exp -ik— + exp ik— = k2y(x+x0)V     V R У     V R yyv     V r У      V r УУ

- 4Const R ² . ^f, a ( ^x + ^x 0 )¹ . f, ay 1 „ ,^f, a ( ^{x + x} 0 )¹ • f, by 1 —-— ------ sin k ------- sin k— =- 4 ab Const sinc k ------- sinc k— .

k2 y (x+x 0)    V R У V R У                  V R У V R У

Формула Б.9 представляет собой параксиальное приближение.

Работа выполнена при поддержке гранта РНФ 1431-00014.