Моделирование панельного флаттера в рамках асимптотической теории течений вязкого газа

Рассматривается обтекание плоской пластины сверхзвуковым потоком вязкого газа. Декартова система координат связана с пластиной, ось ОХ направлена вдоль поверхности пластины, ось ОҮ по нормали к поверхности. Предполагается, что на расстоянии I от передней кромки расположен гибкий участок, имеющий длину d.

Вводятся следующие обозначения для координат, отсчитываемых вдоль поверхности пластины и по нормали к ней, времени, компонентов вектора. скорости, плотности, давления, полной энтальпии, коэффициента, вязкости: 1х, Ру, lt/и^, и^и, и^и, р^р, р^и^р, и^Н/2, р_юр соответствен но. Индекс то относится к размерным параметрам невозмущенного набегающего потока. Предполагается, что число Рейнольдса, велико, но не превосходит критического значения, так что сохраняется ламинарный режим течения.

В зависимости от соотношения геометрических параметров и числа. Re возможны различные режимы течения. При воздействии возмущения давления с амплитудой Ар ^ 1 меняется толщина, вытеснения пограничного слоя, при этом основной вклад в это изменение вносит пристеночная область с малыми скоростями [1]. При нелинейном воздействии на пристеночное течение изменения скорости можно оценить, как Аи ~ и ~ Ар¹/². Эта оценка верна, если влияние сил вязкости здесь в первом приближении несущественно.

«Московский физико-технический институт (национальный исследовательский университет)», 2019

При нелинейных изменениях скорости толщина пристеночной области сдвигового течения также меняется в главном члене, что следует из условия сохранения расхода. Тогда из оценки для продольной скорости у ~ еп, е = Re^-1/² следует и оценка для изменения толщины вытеснения Ау ~ еАр^1/2. При этом существенно, что основная часть пограничного слоя с конечными скоростями дает существенно меньший вклад в суммарное изменение толщины вытеснения Аб ~ еАр, поскольку изменения скорости здесь при малых амплитудах давления линейны.

Если возмущения, вносимые во внешний сверхзвуковой поток можно оценить по формуле Аккерета, и эти возмущения имеют тот же порядок, что и исходное возмущение давления, инициирующее процессы взаимодействия, тогда Ар ~ еАр1/2/Аж. Оценка для величины давления непосредственно определяет и длину области возмущенного течения Аж ~ е/Ар1/2. Отсюда следует, что для всех малых возмущений давления длина области возмущенного течения превосходит толщину пограничного слоя, что и предопределяет возможность использования формулы Аккерета для определения индуцированного возмущения давления.

Предположение о влиянии вязкости в области нелинейных изменений скорости приводит к известным оценкам теории свободного взаимодействия [1]. Ниже рассмотрен режим, для которого влияние вязкости в первом приближении несущественно. При малых возмущениях такой режим реализуется, если амплитуда давления удовлетворяет неравенству е1/2 << Ар << 1.

В этих условиях в поле возмущенного течения можно выделить 4 характерные области. Первая область содержит струйки тока невязкого сверхзвукового течения, характерный поперечный размер этой области определяется длиной этой области и наклоном характеристик, тогда для конечных чисел Маха уі ~ е/Ар1/2.

Область 2 - это основная часть пограничного слоя. На дне этой области расположена область нелинейных возмущений продольной скорости (область 3), в которой влияние вязкости в первом приближении несущественно. Для учета влияния вязкости необходимо ввести в рассмотрение область 4, поперечный размер которой оценивается из условия баланса сил вязкости и инерции у4 ~ е3/2/Ар1/2. Следует отметить, что возможность существования предполагаемой структуры течения зависит от существования безотрывного течения в локальном пограничном слое (область 4).

2.    Формулировка краевой задачи

Решение в области 3 можно записать в следующем виде, основываясь на полученных выше оценках:

ж = жз/pW/2а1/2/ЗАр1/2,(1)

У = р—1/2а-1Ар1/2 уз,(2)

t = а-1/!-1 Ар-1t3,(3)

п(ж, у, t, е, Ар) = г^о№1/2Ар1/2из(жз, уз, t3) + ...,(4)

г(ж, у, t, е, Ар) = г^о№1/2а-1/2!Арз/2гз(жз, уз, tз) + ...,(5)

р(ж, у,t,е, Ар) = 1/(7^^) + Аррз(жз, tз) + ...,(6)

Р = Pw + ...,(7)

где параметр а определяется из решения для течения в невозмущенном пограничном слое а = ди/ду^ Следует отметить, что этот параметр по порядку величины равен O(Re1/2). Подстановка выражений (1) - (7) в систему уравнений Навье-Стокса в результате предель- ного перехода Re ^ то, Ар ^ 0, ApRe1/4 ^ то приводит к системе уравнений:

дпз ,    дпз ,    дпз , дрз + п3    + Гз    + -— = 0, діз      дхз     дуз   дхз (8) дпз , дг --+ X— = 0, (9) дхз дуз др3=0 (Ю) с краевыми условиями х ^ -то : уз = 0,пз = уз.

Решение можно искать в виде пз = уз + Аз(хз , із ) .

Уравнения (8) - (10) тогда можно привести к виду

⁸-А + а^ + £ = 0, ді дх дх

(И)

где нижний индекс «3» опущен.

Физический смысл функции А - это изменение толщины пограничного слоя, взятое с обратным знаком. Во внешнем потоке это изменение индуцирует возмущение давления дА дх

Ар =

Мы предполагаем, что либо рассматриваются малые времена процесса, либо отрыв по давлен тем или иным способом. В условиях, когда часть пограничного слоя находится над гибким участком поверхности, суммарное изменение толщины вытеснения будет определяться изменением толщины пограничного слоя и деформацией поверхности w.

Тогда система уравнений для двух областей имеет вид д дА dw дх дх'

д А ^дА      др ді дх    ш дх .

К этой системе следует добавить уравнение, описывающее деформацию гибкого участка [2], чтобы окончательно получить замкнутую систему уравнений:

д 4w  ^2 2w д2^м пдх4 -n2^ + СИ2 + р(х,і)=0,(14)

где w есть прогиб пластины.

Кроме того, необходимо уравнение для кинематической связи параметров в области 3 и пластины:

— = Vw -А—.15

ді          дх

Из (12) - (15) получаем систему уравнения для w, А:

' ^д⁴ w ^д ²w   ^2 ² w дА 2w

• < дх⁴ дх² ді2    дх   дх ,

дА  ^дА  д² А  д ²w   2w  ^dw

• - ді дх   дх²   дх²    ді дх

с граничными условиями

—Z/2 < х < Z/2, w(х, t = 0) = уі(х); w(х = ± 1 ,і ) = 0, дw(х = ± 1 ,і )   „ дw(х,i = 0)      , .

-----дх------= ^0;----- 8І -----= ^92(х)'

, .         .       . . дА(х ^ ±то, t)

= 0,

А(х, t = 0) = дз (х); —, где D = ЕҺ3/ (12(1 — г2)) - цилиндрическая жесткость, N = No + Nx, No - натяжение, Nx = ЕҺ Jo"     ) йх - натяжение за счет прогиба пластины, Е - модуль Юнга,

2а 0 \дх

Һ - толщина пластины, v - коэффициент Пуассона.

Для простоты будем решать систему уравнений (16) ров D, N, С.

для безразмерных парамет-

д4ш диссипативность и стремит-д2ш имеет дестабилизующии дх2

• ■  .■ - производная четвертого порядка имеет большую

3.

Решение линейной задачи

Линеаризуя систему уравнений (16), получим более простую систему уравнений:

' ^д ⁴ш ^уд²ш     d²w дА дш

< дх⁴ „ дх²      д1²    дх   дх     ,

дА д²А  д²ш дш _                                ^{v 1}

- ді    дх²    дх²    д1 ^.

дх4

ся стабилизовать колебание, а производная второго порядка

, ,                                                                    . дА эффект. Нелинейный член в уравнении Бюргерса А—— характеризует процесс передачи дх дш энергии от длинных волн к коротким волнам, нелинейный член А—— соответствует взаи-дх модействию пластины с потоком газа.

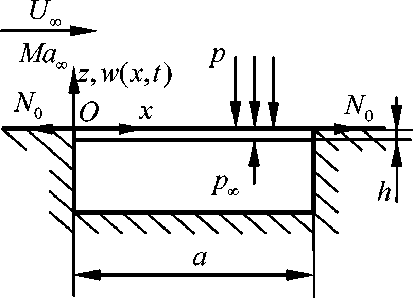
Рис. 1. Схема, пластины

Для того чтобы исследовать устойчивость решения последней системы уравнений, мы ищем возмущение толщины пограничного слоя и прогиб пластины в виде малых бегущих волн:

А - А0е1^кх);ш ~ е1^-^, где Ао есть комплексное число. Это приводит (17) к виду

( —ш² + Dk⁴ + Nk² + Аогк — гк = 0, 1 — Аогш — к² — Аок² — гш = 0.

Напишем Ао в виде Ао = а + Ьг, где а, Ь есть вещественные числа, получим выражение для прогиба, пластины:

к2 (2Ь + (1 — а2 — Ь2) г)

ш = -

Ь² + (а + 1)²

Для того чтобы A, w не возрастали со временем, мнимая часть частоты ш должна быть меньше либо равняться нулю !т(ш) < 0, это соответствует условию а² + Ь² > 1.

После нескольких математических преобразований получим следующую систему уравнений:

(4Ь2 - (а2 + Ь2 - 1) ) _ Dk3 + Nk — Ь (ь2 + (а +1)2)     "

4Ь (1 — а2 — 2)а

(Ь2 + (а + 1)2)2 "'

С помощью пакета Matlab [3] показано, что для всех волновых чисел k всегда существуют растущие моды. При D = 1, N = 1, k = 1 максимальный инкремент нарастания равен 0.4188 и частота — гш_тах = 0.4188 + 1.6939г. С другой стороны, с помошью спектрального метода [4] можно привести систему линейных дифференциальных уравнений в частных производных к системе обыкновенных дифференциальных уравнений. Найдя все ее собственные числа, также получим растущую моду с наибольшим инкрементом нарастания, который равен 0.4188. Совпадение результатов подтверждает достоверность обоих методов.

При увеличении волнового числа максимальный инкремент нарастания уменьшается по линейному закону, а частота возрастает по квадратичному закону. При D = 1, N = 1, k = 5 получается — гш_тах = 0.1 + 25.6г. а. при D = 1, N = 1, k = 10 получается —гш_тах = 0.05 + 100г. Из этого следует, что неустойчивые моды длинных волн нарастают быстрее, чем неустойчивые моды коротких волн.

4. Решение нелинейной задачи

Дальше рассмотрена нелинейная задача, область пластины —1/2 < ж < 1/2, область расчетов —20 < ж < 20. Расчет проводится с помощью разностной схемы третьего и четвертого порядков точности и метода Рунге-Кутта второго порядка точности.

Исследуется влияние дискретизации по времени и пространству на расчет, показано, что значения dx = 1е—2, dt = 1е—5 обеспечивают необходимую точность решений, поэтому для дальнейших расчетов используются последние дискретизации по времени и пространству.

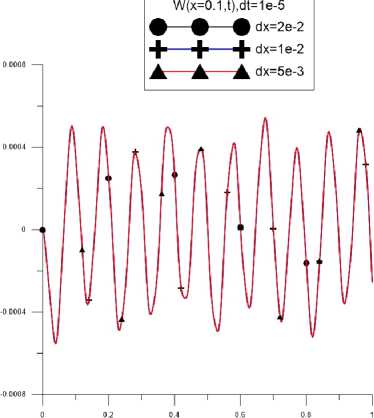
Рис. 2. Дискретизация по пространству

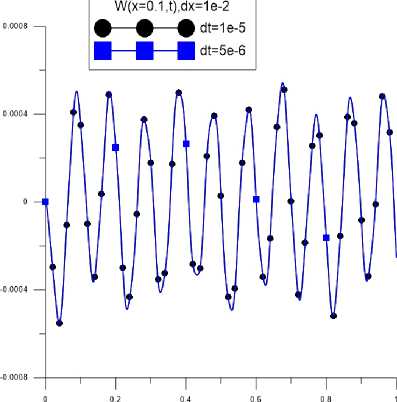
Рис. 3. Дискретизация по времени

На рис. 4 представлены результаты, полученные с помощью быстрого преобразования Фурье. Видно, что существуют две главные моды. С помощью метода главных компонен- тов [5] выясняется, что существуют 4 главные моды, что эти моды содержат более 99% энергии колебаний пластины.

Представлены нормальные моды колебания, видно, что все эти колебания представляют собой комбинацию синусов и косинусов. Дальше представлено сравнение результатов преобразования Фурье и их главных мод, совпадение результатов подтверждает точность обоих методов.

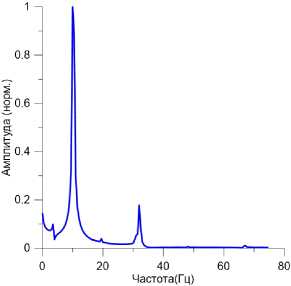
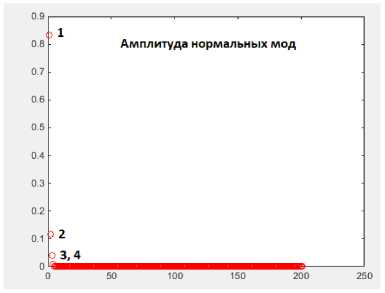
Рис. 4. Преобразование Фурье колебания пласти- Рис. 5. Нормированные амплитуды нормальных

ны при х = 0.1

главных мод

Дальше показано влияние цилиндрической жесткости на колебание пластины. При D = 10 нелинейный член при производной второго порядка играет несущественную роль, поэтому колебание является регулярным. При D = 10^-2 член при производной четвертого порядка мал, поэтому нелинейный член при производной второго порядка играет главную роль, так что колебание станет более сложным. Преобразование Фурье, фазовый портрет, вид главных мод при х = 0.1 доказывают это рассуждение.

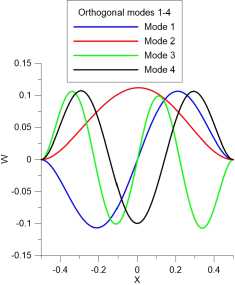
Рис. 6. Главные нормальные моды

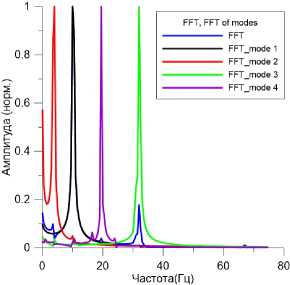
Рис. 7. Преобразование Фурье и их главных мод

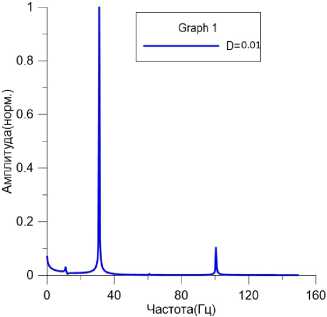
Рис. 8. Преобразование Фурье D = 0.01

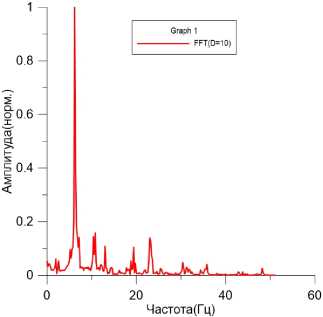
Рис. 9. Преобразование Фурье D = 10

При D = 1е — 3 поведение пластины станет еще более сложным, с помощью метода Бубнова-Галеркина можно привести уравнение колебания пластины (уравнение фон Кармана) к системе обыкновенных дифференциальных уравнений. Разложим решение для прогиба пластины по собственным формам колебаний пластины W j (х) в вакууме с неизвестными амплитудами Aj (t):

∞

^w(x,t) = ^ ^Wj ⁽x)^Aj ⁽t).

^j =1

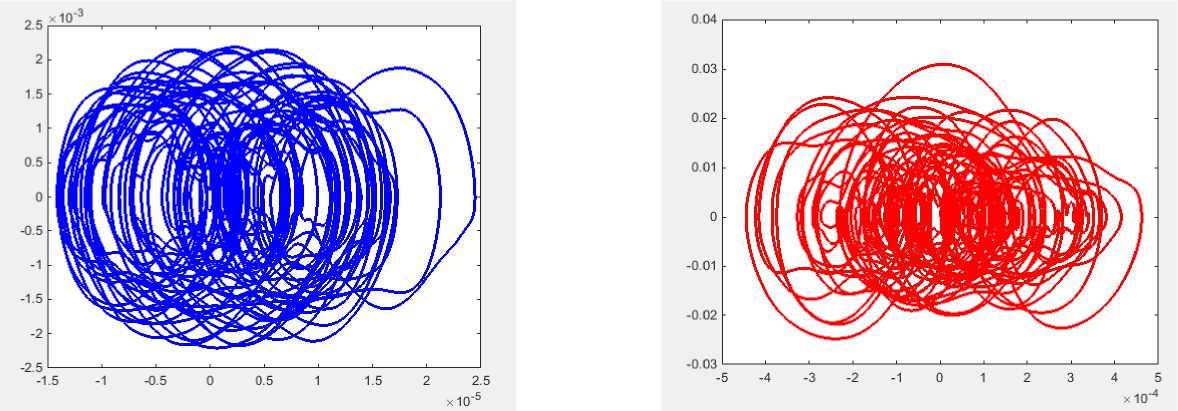
Рис. 10. Фазовый портрет D = 0.01

Рис. 11. Фазовый портрет D = 10

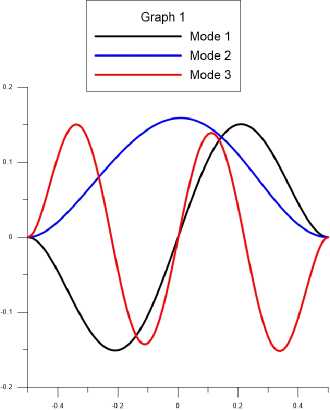
Рис. 12. Главные моды D = 0.01

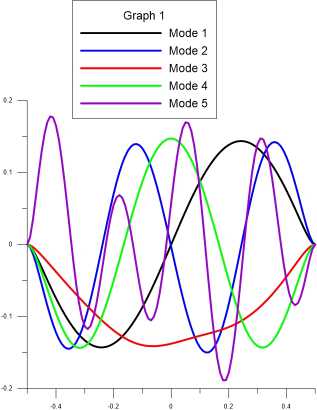
Рис. 13. Главные моды D = 10

Подставим последнее выражение для прогиба пластины в уравнение фон Кармана в вакууме:

_. д⁴ w             д ² w    д 2w dw

^D^ ^{— (No} + ^N" ^} ы + ^с^ + дХ = ^0,

™ с .1 n _а(*^

Умножим последнее уравнение на W" (х) и проинтегрируем по х от —Z/2 до Z/2. В силу ортонормированности собственных функций получим следующее уравнение для п-й амплитуды [6]:

дА ²   2  „    _ А       .       .

dt2—+ “ 0" А" + 12D Е ^mkdjTi^АтА_кА₃ = 0, m,k,j =1

где

^^1/2 / d4Wj

-Z/2 1 ^дх4

-

No

д ²Wj дх²

^— ІЦ¹) ^W" ^dx = “2" ⁸i ’

Г 1/2

¹   Wj W_ndx — д",

-1/2

д" - символ Кронекера, a j" —

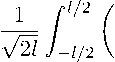
dWj м Эх Эх

) dx — —Д f'2 ( д 2W,

—W" ) dx.

дх2    /

)         V2i ./-Z/2 V

Считаем, что |А„| << |А1|,п > 1 и amn << a11 ,т,п > 1, тогда в уравнении для Ai можно отбросить все члены, которые содержат амплитуды с индексом выше 1. Тогда уравнение для Ai запишется в виде дА? dt2

+ w0iAi + Ka2iA3 — 0,

где К — 12D.

Это есть известное уравнение Дюффинга, будем искать приближенное решение в виде асимптотического разложения типа Пуанкаре [7]:

П — По + ЕП1 + Е2П2..., 2            2 ,            ,     2

Шо1 — Ш + ЕС1 + Е С₂... .

Подставив разложение в уравнение Дюффинга, разложив по степеням е — К Ah и приравняв коэффициенты при одинаковых степенях, получим следующие задачи для определения по, п1;

По + ш2ио — 0, по(0) — а, по(0) — 0,

П1 + Ш²и1 + С1по + п3, пі (0) — 0, п 1(0) — 0.

Решение уравения (22): ио — a cos(шt)

Подставляя значение ио в уравнение (23) и используя тригонометрическое тождество cos(3x) — 4cos(x)3 — 3cos(x), получим и1 + Ш2и1 + а(с1 + 3А2/4) cos(wt) + a3 cos(3шt)/4 — 0.

Отбросим вековой член, тогда ci — —3а2/4. Для первого приближения

Ш21 — Ш2 + ЕС1, ш — Ш21 — 3ео?/4.

Тогда получим решение уравнение Дюффинга в первом приближении:

п — а cos(шt) + а3/32 cos(3шt), где ш — ^Ш21 — 3Еа2/4, е — 12Da21.

Из этого следует, что первая мода содержит две гармоники с частотами шt, 3шt. Кроме того, из [6] также следует, что наблюдается внутрений резонанс между двумя первыми модами колебания пластины. Это подтверждает достоверность расчета колебания пластины, как и показано ниже.

Из графика видно, что для первой моды

Ш11 — 6.2, Ш12 — 18.8, Ш12 ~ 3 шц.

Наблюдается внутрений резонанс двух первых мод:

<22 = 2.1, <11 = 6.2, <21 = 10.4, <23 = 14.6, с^12 = 18.8, <24 = 23,

<22 : <11 : <21 : <23 : <12 : <24 ~ 1:3:5:7:9:11.

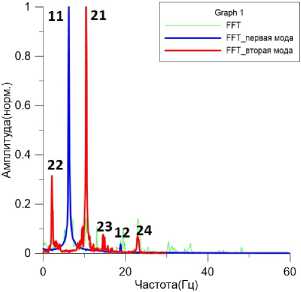
Рис. 14. Внутрений резонанс между двумя первыми модами колебания

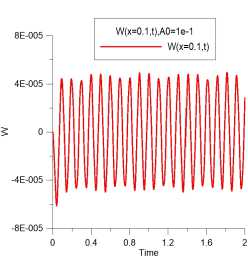
Рис. 15. Колебание пластины

D = 1, А = 0.1, ж = 0.1

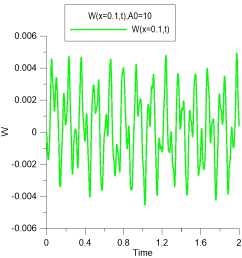
Рис. 16. Колебание пластины

D = 1, А =10, ж = 0.1

Бифуркационная диаграмма

Рис. 17. Бифуркационная диаграмма для локальных амплитуд колебания

Дальше исследуется влияние амплитуды возмущения толщины вытеснения пограничного слоя. Ясно, что увеличении амплитуды возмущения толщины пограничного слоя приводит к заметному нелинейному эффекту.

При А = 10 наблюдается бифуркация локальных амплитуд колебаний пластины (рис. 17) за счет сильной нелинейности.

5.    Заключение

Получены следующие выводы.

• 1.    Существует критерий выбора главных мод колебания, заключающийся в том, что такие моды содержат более 99% энергии колебания. Зная эти моды, можно управлять колебанием пластины.

• 2.    Наблюдается внутрений резонанс 1:3и1:3:5:7:9:11 между двумя первыми модами за счет нелинейности колебания пластины.

• 3.    При увеличении амплитуды возмущений толщины вытеснения пограничного слоя и уменьшении цилиндрической жесткости наблюдается нерегулярное поведение колебания за счет нелинейности члена при производной второго порядка прогиба пластины.