Моделирование параллельных алгоритмов шифрования информации
Автор: Кочеров Ю.Н., Червяков Н.И.
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Электромагнитная совместимость и безопасность оборудования
Статья в выпуске: 4 т.10, 2012 года.
Бесплатный доступ
В статье рассмотрены вопросы моделирования параллельных алгоритмов шифрования информации с использованием системы остаточных классов и приведены примеры алгоритмов шифрования RSA, восстановления чисел и моделирования параллельных алгоритмов шифрования в среде Matlab Simulink. Целью статьи является увеличение криптостойкости путем параллельного выполнения различных криптографических алгоритмов или параллельного использования одного алгоритма, но с разными ключами.
Параллельные алгоритмы, шифрование информации, алгоритм rsa
Короткий адрес: https://sciup.org/140191592
IDR: 140191592 | УДК: 621.391
Текст научной статьи Моделирование параллельных алгоритмов шифрования информации
В современном информационном мире информация становится более ценным ресурсом, чем материальные и энергетические ресурсы. Владение точной и достоверной информацией дает преимущество той стороне, которая ею владеет, – особенно если эта информация касается конкурентов. Обладание такой информацией позволяет ее владельцу получить выигрыш: материальный, политический или военный. В современном мире необходимо защищать огромное количество информации, хранимой в базах данных и предаваемой по информационным сетям.
Постановка задачи и моделирование алгоритма шифрования RSA в среде Matlab Simulink
В настоящее время наиболее важную роль играет защита электронной информации от несанкционированного доступа. Для защиты информации используют различные криптографические алгоритмы, такие как RSA, DSA, ГОСТ 2814789, Шифросистема Эль-Гамаля и многие другие.
Надежность криптографических алгоритмов во многом зависит от сложности реализации и от длины ключа шифрования данных. При моделировании в системе Matlab Simulink был использован алгоритм шифрования RSA – криптографический алгоритм с открытым ключом (RSA стал первым алгоритмом такого типа, пригодным и для шифрования и цифровой подписи, сегодня он используется в большом числе криптографических приложений [1]).
Возьмем два больших простых числа
р и q
. Определим
n
как результат умножения
p
на
q'.n = р • q.
Выберем случайное число, которое назовем
d
: это число должно быть взаимно простым (не иметь ни одного общего делителя, кроме единицы, с результатом умножения
ip_W_XW
Определим также число e , для которого является истинным следующее соотношение (e • d) mod( p -1) • (q -1) = 1. Назовем открытым ключом числа e и n, а секретным – d и n. Задача состоит в том, чтобы зашифровать текст, рассматриваемый как последовательность чисел м^ , по формуле С(Г) = (MdY^modn . Чтобы расшифровать данные, необходимо выполнить вычисления M(i) = (C(z/) mod и . В результате будет получено множество чисел M(i) , которые представляют собой исходный текст.
Следующий пример наглядно демонстрирует алгоритм шифрования RSA.
Зашифруем и расшифруем сообщение «САВ» по алгоритму RSA. Для простоты возьмем небольшие числа, что сократит расчеты.
Выберем p = 3 и q = 11.
Определим 77 = 3'11 = 33.
Найдем (^-IH^-ll^O. Пусть d будет равно, например, 3, то есть d — 3 .
Выберем число e по формуле: (е • 3)mod 20 = 1. В нашем случае e будет равно, Т. (е = 7). Представим шифруемое сообщение как последовательность чисел в диапазоне от 0 до 32. Буква ^ = 13, 5 = 17, С = 19. Теперь зашифруем сообщение, используя открытый ключ {7,33}:
С1 = (13 7)mod 33 = 62748517 mod 33 = 7;
С2 = (177) mod 33 = 410338673 mod33 = 8;
СЗ = (197)mod33 = 893871739 mod 33 = 13.
Теперь расшифруем данные, используя закрытый ключ {3,33}:
Ml = (73)mod33 = 343mod33 = 13 (A);
Л72 = (83)mod33 = 512mod33 = 17 (B);
М3 = (133)mod33 = 2197mod33 = 19(C).
Данные расшифрованы [2].
Примеры моделирования алгоритмов RSA в Matlab Simulink представлены на рис. 1-2.
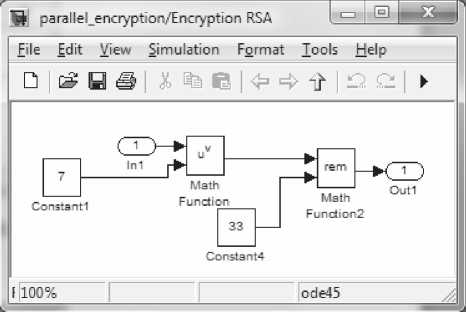
Рис. 1. Пример моделирования шифрования алгоритма RSA
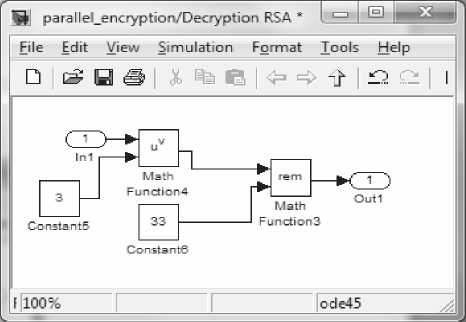
Рис. 1. Пример моделирования дешифрования алгоритма RSA
Использование СОК для разделения информации на модули и и восстановления ее
Для параллельного использования нескольких алгоритмов шифрования необходимо представить входную информацию в системе остаточных классов (СОК). Система остаточных классов дает нестандартное представление для чисел и используется для повышения эффективности операций над кодами в остатках. Дело в том, что в данной системе числа представляются своими остатками от деления на выбранную систему оснований и все рациональные операции могут выполняться параллельно над цифрами каждого разряда в отдельности. После представления информации в СОК она шифруется алгоритмами RSA (пример работы алгоритма см. выше).
Для передачи данных после шифрования по одному каналу и разделения входного сигнала на отдельные составляющие используются, соответственно, блок мультиплексора и блок демультиплексора. Основным параметром мультиплексора является число входов, демультиплексора – число выходов [3-4]. Примеры использования мультиплексора и демультиплексора представлены на рис. 3.
На входы мультиплексора подаются два сигнала разной частоты, представленные двумя графиками: мультиплексор коммутирует их на один выход, скоммутированные сигналы в один канал представлены графиком. Далее демультиплексор коммутирует сигнал со входного канала на два выходных сигнала, также представленные графиками.
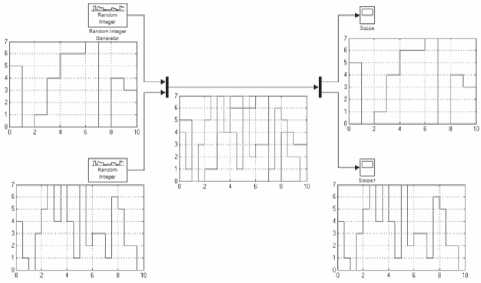
Рис. 3. Пример использования мультиплексора и демультиплексора
После дешифровки данных, чтобы получить исходную информацию, использовалось преобразование СОК → ПСС, где ПСС – позиционная система счисления. При преобразовании СОК → ПСС использовался метод ортогональ- ных базисов. Преобразование кода числа А, заданного в СОК, в ПСС можно осуществить в соответствии с выражением, записанным в виде 4 = (^ Следующий пример демонстрирует преобразование из остаточных классов в позиционный код. Возьмем число Л = 103. Дана система оснований Pi=2, p2=3, p3 =5, pA=T, p5 =11, объем диапазона равен P = 2-3•5•7 • 11 = 2310. Представим число A в системе остаточных классов по системе оснований p, A = (1,1, 3,5,4). Для расчета ортогональных базисов найдем величины P : i „ p 2310 „ P 2310 p\ = — = : 1155; Л, = — =-----= 770 ; P\ 2 " P2 3 „ p 2310 „ P 2310 p3 = — = = 462 ; P4 = — =----= 330 ; Рз 5 Pa 7 n p 2310 p5 = — -- = 210. Рз 11 Ищем веса базисов: 1155 ■ mx = l(mod2), методом подбора находим mA = 1; 770- m2 = l(mod3), методом подбора находим m2ее 2; 462 • m3 = l(mod5), методом подбора находим m3 = 3; 330-w4 = I(mod7), методом подбора находим m4 = 1; 210- m5 = l(modl 1), методом подбора находим m5ее 1. Далее вычислим сами базисы: 5, = m, • 7^ = 1 ■ 1155 = 1155; B2=m2-P2 =2-770 = 1540; B, = m3-P3 =3-462 = 1386; B4 = m4 • P4 = 1 • 330 = 330; B5=m5-P5 =1-210 = 210. Далее, имея значения базисов, вычислим значения числа А: АЦ 1-1155 + 1-1540 + 3-1386 + 5 • 330 + + 4-210 I2310 = |9343|23io =ЮЗ. Из расчета видно, что переведенное из СОК число идентично исходному числу. Моделирование параллельных алгоритмов шифрования в среде Mathlab simulink На рис. 4 приведен пример модели параллельных алгоритмов шифрования при моделировании в среде Matlab Simulink. Рис. 4. Модель параллельных алгоритмов шифрования При моделировании в среде Matlab исходная информация разбита на пять модулей ^ = (2,3,5,7,11). Каждый модуль зашифрован алгоритмом RSA. Алгоритм, представленный на рис. 4, можно условно разбить на пять частей. В первой части входной сигнал представляется в СОК по системе оснований p = (2,3,5,7,11). Во второй части информация, представленная в СОК, параллельно шифруется алгоритмами RSA. В третьей части сигнал после шифрования для передачи данных по одному каналу коммутируется мультиплексором в один канал, и для дешифровки данных ско-мутированный сигнал разделяется демультиплексором на пять каналов. В четвертой части сигнал дешифруется. В пятой части сигнал восстанавливается из СОК. Проверка на правильность выполнения путем вычитания входной и выходной информации. Рассмотрим пример использования параллельных алгоритмов шифрования. Зашифруем сообщение «АВС», используя параллельные алгоритмы шифрования. Представим сообщения как последовательность чисел A = 13,5 = 17,C = 19. Представим сообщение в СОК по системе оснований p = (2,3,5,7,11); A = (1,1,3,6,2); B = (1,2,2,3,6); C = (1,1,4,5,8). Зашифруем сообщение, представленное в СОК, используя для каждого модуля свой ключ. Для числа по модулю 2 мы будем использовать открытый ключ {7,33} и закрытый {3,33}, для модуля числа 3 открытый ключ {11,91} и закрытый {59,91}, для модуля числа 5 открытый ключ {17,65} и закрытый {113,65}, для модуля числа 7 открытый ключ {5,34} и закрытый {13,34} и для модуля числа 11 открытый ключ {29,437} и закрытый {41,437} – пример расчета ключей см. выше. При моделировании в среде Matlab Simulink, так как значения переменных при возведении в степень выходили за область определения, во всех алгоритмах шифрования использовались одинаковые ключи шифрования: открытый ключ {7,33} и закрытый {3,33}. Теперь зашифруем сообщения, используя данные ключи: СЛ1 = (l7)mod33 = 1; СВ1 = (l7)mod33 = 1; Ccl = (l7)mod33 = 1; CA2 = (l")mod91 = 1; Cs2 = (2n)mod91 = 46; Cc2 = (ln)mod91 = 1; C43 = (317)mod65 = 48; CB3 = (217)mod65 = 32; Cc3 = (4l7)mod65 = 49; CA4 = (65)mod34 = 24; Cs4 = (35)mod34 = 5; Cc4 = (55)mod34 = 31; Ca5 = (229)mod437 = 243; CB5 = (629)mod437 = 302; Cc5 = (829)mod437 = 12. Итак, зашифрованное сообщение примет вид CA = (1,1,48,24,243); CB = (1,46,32,5,302); Cc =(1,1,49,31,12). Далее расшифруем сообщение: MA1 = (l3) mod 33 = 1; MB1 = (I3) mod 33 = 1; Mc\ =(l3)mod33 = l; MA2 = (l59)mod91 = 1; MB2 = (4659)mod91 = 2; Mc2 = (l59)mod91 = 1; MA3 = (48113)mod65 = 3; MB3 = (32113)mod65 = 2; Mc3 = (49ll3)mod35 = 4; MA4 = (24l3)mod34 = 6; MB4 = (513)mod34 = 3; Mc4 = (3113)mod34 = 5; MAS = (24341)mod437= 2; MB5 = (302”)mod437= 6; Mc5 = (1241)mod437 = 8. Расшифрованное сообщение примет вид MA = (1,1,3,6,2) = A; MB = (1,2,2,3,6) = в; Mc = (1,1,4,5,8) = C . Таким образом, после расшифровки мы получили исходное сообщение. Восстановим расшифрованное сообщение преобразованием СОК → ПСС (пример преобразования СОК → ПСС см. выше). A = |1 • 1155 + 1 -1540 + 3 -1386 + 6 • 330 + 2 • 210|^3w = = I92531,,» =13 ■ В = |2 ■ 1155 + 2 ■ 1540 + 2 ■ 1386 + 3 ■ 330 + 6 ■ 210|^310 = = I9257 lMM =17 ■ C = |1 -1155 + 1 -1540 + 4 -1386 + 5 - 330 + 8 ■ 210|7310 = -111560 |2,|0 =19 . Сравним данные, зашифрованные простым алгоритмом RSA, и данные, полученные при использовании параллельных алгоритмов шифрования. В примере для шифрования использовались одинаковые сообщения «АВС», при использовании алгоритма RSA мы получили следующее сообщение C1 = 7,C2 = 8,C3 = 13. При использовании параллельных алгоритмов шифрования мы получили сообщение CA = (1,1,48,24,243); CB = (1,46,32,5,302); Cc =(1,1,49,31,12). Выводы Данные, зашифрованные при помощи параллельных алгоритмов шифрования, имеют достаточно сложную структуру. Получение исходной информации из зашифрованной усложняется необходимостью взломать каждый алгоритм отдельно. Исследования выполнены при поддержке гранта РФФИ 12-07-00482-а.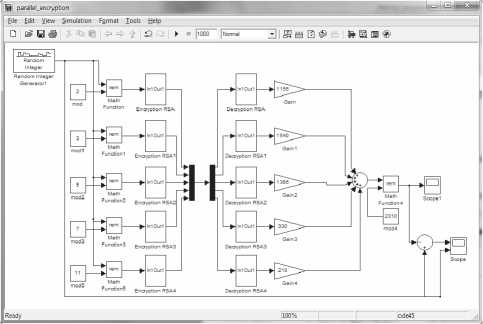
Список литературы Моделирование параллельных алгоритмов шифрования информации
- http://www.anti-malware.ru/rsa
- http://www.e-nigma.ru/stat/rsa/
- http://subscribe.ru/archive/tech. digitchip01/200212/19092116.html
- Черных И.В. Simulink: инструмент моделирования динамических систем//http://www. knigka.info/2008/10/03/simulink-instrument-modelirovanija.html
- Модулярные параллельные вычислительные структуры нейропроцессорных систем. Под. ред. Н.И. Червякова. М.: Физматлит, 2003. -288 с.
- http://www.cybersecurity.ru/crypto/85133.html


