Моделирование перехода плоского вращательного движения космического аппарата с асимметрией в колебательное при входе в атмосферу

Самарский государственный аэрокосмический университет

Рассматривается движение относительно центра масс космического аппарата с малой асимметрией, восстанавливающий аэродинамический момент которого описывается рядом Фурье по углу атаки с двумя первыми синусоидальными и первым косинусоидальным членами. Найдено решение для угла атаки в невозмущенном вращательном движении. Моделируется переход плоского вращательного движения аппарата к колебательному, обусловленный медленным изменением коэффициентов моментной характеристики, а также наличием и медленным изменением коэффициентов малой асимметрии и демпфирования. Получено аналитическое выражение для интеграла действия, взятого вдоль сепаратрис, разделяющих вращательную и колебательные области фазового портрета системы. Получены аналитические формулы для определения времен перехода вращательного движения в колебательное, а также критической угловой скорости внеатмосферного вращения, при превышении которой вращение аппарата продолжается в течение длительного интервала времени (возникает плоская авторотация).

Постановка задачи

Рассматривается плоское движение неуправляемого космического аппарата (КА) на верхнем участке траектории спуска в атмосферу, когда можно пренебречь изменением скорости центра масс и угла наклона траектории. Исследуются случаи, когда в процессе спуска вращательное движение переходит в колебательное или имеет место длительное вращение без перехода в колебательное движение (плоская авторотация). В [1] рассматриваются переходные режимы движения КА с синусоидальной, а в [2] с бигармонической моментной характеристикой без учета влияния малой асимметрии. В [3] исследуются условия возникновения плоской авторотации асимметричного КА, моментная характеристика которого представлена рядом Фурье. Получены в интегральном виде формулы для определения критического значения начальной угловой скорости вращения КА, при которой реализуется плоская авторотация. В данной работе рассматривается плоское движение относительно центра масс КА с малой массовой асимметрией, вызванной поперечным смещением центра масс, и аэродинамической асимметрией, обусловленной искажением поверхности аппарата. Пусть момент от указанной асимметрии может быть представлен в виде четного ряда Фурье по углу атаки с постоянным членом (средним значением момента) и первым косинусоидальным членом. Тогда, добавляя косинусоидальную компоненту к основному восстанавливающему аэродинамическому моменту, описываемому нечетным рядом Фурье с двумя первыми гармониками [2], считая среднее значение момента асимметрии и значение демпфирующего момента малыми величинами, учитывая, что коэффициенты моментов медленно меняются во времени из-за медленного изменения плотности атмосферы в процессе спуска, движение КА можно описать следующим уравнением [2, 4]

a + a (z)sin a + b ( z ) sin 2 a +

+ c (z )cos a = ec( z )a + e^( z), (1) где a - угол атаки; a(z), b(z),c(z) - коэффициенты моментной характеристики; o(z) и £(z) - усредненные по углу атаки коэффициенты демпфирования и асимметрии; z -медленно меняющийся параметр, переменность которого связана с медленным изменением плотности атмосферы в процессе спус- ка; £ - малый параметр, характеризующий малость коэффициентов демпфирования и асимметрии.

Коэффициенты уравнения движения (1), если зависимость плотности атмосферы от высоты полета аппроксимировать экспонентой, могут быть представлены в виде [2, 4]:

a ( z ) = а о z , b(z) = b ₀ z , c(z) = c ₀ z , o ^(z) = o о ^z , ^{S (z)} = ^S о ^z , а о =- m . SlV^ p (t o )/ ( 2 1 ) , b о =- m b SIV^t , )/ ( 2 1 ) , c о = -A yC_я SIV2p(t о )/ ( 2 1 ) ,

S . = ( A yC т о +A m₌W}p(t о )/ ( 2 1 ) , a „ = (m " 1 ² /I - C Jо / m)SV , p (t о )/ 2, z = exp( e (t — t о )) , в = Х V o isin ^e o l , где m_a,m_b - коэффициенты основного восстанавливающего аэродинамического момента; m ® - усредненный по углу атаки коэффициент аэродинамического момента демпфирования; C y _{a о} - усредненная производная по углу атаки коэффициента аэродинамической подъемной силы; C _{т о} , C _{т 1} - первые два члена разложения коэффициента тангенциальной аэродинамической силы в четный ряд Фурье; A m_z - коэффициент аэродинамического момента асимметрии; A у = A у/I - безразмерное смещение центра масс КА от оси его геометрической симметрии; I - характерный размер; S - характерная площадь; I - поперечный момент инерции; m - масса аппарата; V , - скорость полета; 0 _o - угол наклона траектории; p (t_o) - плотность атмосферы в начальный момент времени; X - логарифмический градиент плотности атмосферы по высоте.

Невозмущенное движение КА

В случае невозмущенного движения ( £ = о, z = const ) уравнение движения КА запишется в виде

&& + asin а + bsin 2 а + ccos а = о.   (2)

Следует отметить, что уравнение движения физического маятника по углу его отклонения от вертикали, когда он установлен на вращающейся платформе и точка его подвеса смещена относительно оси вращения платформы [5], имеет вид аналогичный (2).

Для выяснения общих свойств движения системы (2) воспользуемся методом фазовой плоскости. Анализ фазового пространства рассматриваемой системы проведем аналогично [5]. Интеграл энергии системы (2) имеет вид а2

— - acos a- bcos ² а + csin а = h . (3)

Фазовым пространством рассматриваемой системы является цилиндр с координатами а, а . Уравнение (3) определяет связь между а и а, тем самым, является уравнением фазовых траекторий. Из (3) следует, что а = ± V 2(f( а ) + h) , где

f( а ) = acos а + bcos ² а- csin а .  (4)

Экстремальные значения функции f ( а ) соответствуют состояниям равновесия уравнения (2), т.е. особым точкам на фазовом цилиндре а , а .

Из выражения (4) функции f ( а ) следует, что в зависимости от значений параметров a , b , c могут существовать или две, или четыре особые точки. Бифуркационное соот- ab ношение параметров ⁿ = c и ^z = c , разделяющее эти случаи, находится из условия слияния двух особых точек, что осуществляется при одновременном выполнении двух условий:

f ‘ ( а ) = о и f ‘‘ ( а ) = о.

Разрешая эти соотношения относительно П и Z , получаем параметрическое представление бифуркационной кривой П = П ( Z ) :

П = ctg ^За, Z = - ( 2 sin ³ а ) '.    (5)

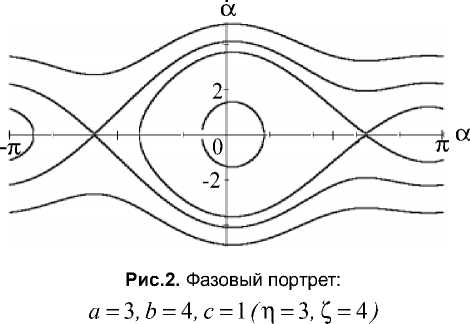
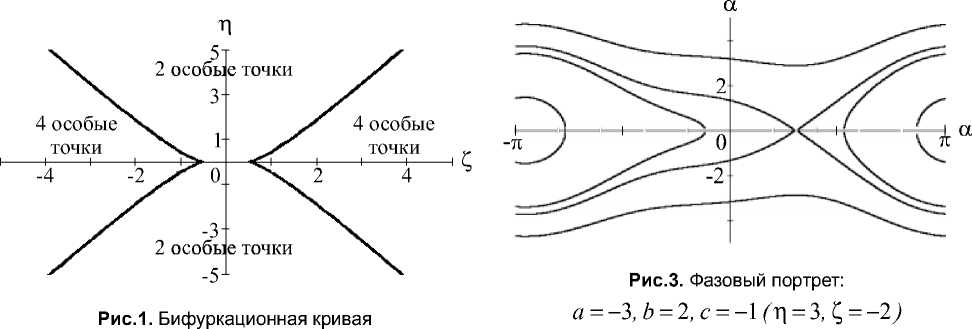
Согласно (5) на плоскости П , Z протекают четыре ветви кривой П = П б Z ) , соответствующие изменению а в интервале [ - п , п ] . Данная кривая, изображенная на рис.1, разбивает плоскость на три области. При пара-метрах П , Z , находящихся внутри области, ограниченной бифуркационной кривой, на фазовом цилиндре имеются две особые точки, а в других областях - четыре особые точки. Для параметров, принимающих значения Z = ± 0,5, П = 0 происходит слияние трех особых точек: при _а = 0 для Z = + 0,5, П = 0 и при а = ±п для Z = — 0,5, П = 0.

На рис.2 показан фазовый портрет системы, когда имеются четыре особые точки, на рис.3 ‒ две особые точки.

Как видно, космический аппарат в зависимости от начальных условий (h) и величин a, b, c может совершать как вращательные, так и колебательные движения, области которых разделены сепаратрисами.

Найдем решение для угла атаки в невозмущенном вращательном движении. Вводя

а

новую переменную ^и = tg — , уравнение (3)

можно записать в виде

dt = ±

du

G(u).

Здесь знак выбирается в зависимости от знака du таким образом, чтобы в любой момент времени правая часть уравнения была неотрицательной. После интегрирования имеем

t

^- t 0

u

= r du

,' 4G6U

U ² = 2 [ h - a + b ] u ⁴ - 2 cu ³ + 2 [ h - b ]и ² -

- 2 cu + 2 [ h + a + b ] = G ( и )

. (6)

Разделяя переменные в уравнении (6), получим

Интеграл (7) относится к классу эллиптических интегралов и приводится к нормальному эллиптическому интегралу Лежандра первого рода [6]. Результат интегрирования зависит от типа корней полинома четвертой степени G ( u ) . В случае вращения все четыре корня полинома комплексные. Введем следующее правило нумерации этих корней: b l ± ic 1 , b 2 ± ic ₂, b i >  b 2 , c₁ >  0 , c ₂ >  0.

Приведение интеграла (7) к нормальному эллиптическому интегралу первого рода осуществляется посредством преобразования

u = u(ф), отображающего интервал интегрирования [u0, u ] в соответствующий интервал действительного аргумента [ф0, ф]. Вид преобразования u = u(ф) зависит от типа и сочетания корней, а также от знака старшего коэффициента полинома G(u) [6]. Для рассматриваемого случая вращения все четыре корня полинома комплексные и преобразование может быть представлено в виде u = b1 + c1 tg (ф+ф,),           (8)

где

⁰ 3 ⁺ ® 4 n            С ) ± С?

^ф • = —-—, 0_{3 4} = arctg —--- ² - острые углы.

²      ' b - b 2

Полагая, что в момент времени t = 10, а = а 0, при этом ап, tg- ф0 = arctg —2

c ₁

Тогда, учитывая (8), интеграл (7) преобразуется к следующему виду:

t— t о = |[F( ф.k) — F( фо,к)],(10)

где

F(ф.к) = 1 /dT.

о у 1 — k sin ф

- эллиптиче ский

интеграл первого рода, к ² = sin ² 0 5 - модуль эллиптического интеграла,

Jh — a + b| ,----     02 cos 0

8= ^v ,------V c i c₂ tg -5 =----- ³ -0_S _

2V cos 0 5 ^v ’     4    cos 0 ₄ ’ 2 ⁵

острый угол.

Обращая эллиптиче ский интеграл, из равенства (10) получим ф = am [8(t — 10) + T0 ,k ],        (11)

где T ₀ = F( ф ₀ ,k) .

Учитывая формулы (8), (11) и то, что а u = tg —, имеем следующее решение для угла атаки во вращательном движении:

а = 2 arctg [ b j + c 1 tg ( am ( 8 (t — 1 ₀ ) + T ₀ ,k ) +ф , ) ] . (12)

Следует отметить, что формула (12) задает непрерывную функцию на отрезке ае [ —п ; п ] . В рассматриваемом случае вращения необходимо продолжить функцию а на соответствующие отрезки, исходя из ее непрерывности.

Возмущенное движение КА

В возмущенном движении с изменением величин коэффициентов a, b, c и наличием возмущений, обусловленных демпфированием и асимметрией, происходит эволюция фазовых траекторий, в результате которой они могут пересекать сепаратрисы, попадая в различные области фазового портрета. Это явление сопровождается качественным изменением характера движения: вращательное движение может переходить в колебательное, колебательное движение может “скачкообразно” переходить в колебательное движение с другими амплитудными характеристиками.

Рассмотрим режим движения, когда КА из вращательного движения переходит в колебательное. В этом случае фазовая точка, двигаясь по фазовому цилиндру, пересекает сепаратрису, разделяющую вращательную и колебательную области. На рис.4 приведен случай такого движения (начальные условия движения:

а0 = —0,02 с"2,     b0 = —0,005 с"2, c0 = —0,005 с"2, ^0 = 0,0008 с"2, с0 = —0,00001 с—1, а0 = 10 град,

(X ₀ = 30 град / с , в = 0,05 с 1 ).

Будем полагать, что критерий применимости асимптотических методов в задачах спуска КА в атмосфере выполняется. Для плоского движения он имеет вид [4]

2 а & ₀

X V ₀ sin 0₀|

2 а & ₀ в

>> 1. (13)

Тогда для описания вращательного движения системы с медленно меняющимися параметрами (1) воспользуемся законом изменения интеграла действия [4]

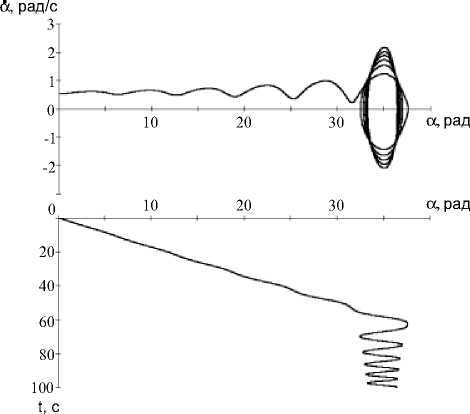
Рис.4. Переход вращательного движения в колебательное

I g = ^£ 0 zI g ^{+ 2 n}^ z ,        (14)

где

I g = j(& d a ,            (15)

-П а а определяется из интеграла энергии (3).

Исключая из уравнения (14) время, принимая t0 = 0 и учитывая, что в этом случае z = exp(вt), получим dig = Q 0 Ig + 2п3 dz в в '

После интегрирования имеем

I_g ( z ) = A - Be ^{- C(z - 1} ) .         (16)

Здесь

A = -2л| 0	B = -	" 2 n^ 0 ,. "	C = - £°.
£ 0    ,		L £ g 0 J	,               в ;

I g 0 = I g (t 0 ) , — значения интеграла действия в начальный момент времени.

В случае, когда на границе атмосферы коэффициенты a, b, c существенно малы по сравнению с угловой скоростью вращения a ₀, начальное значение интеграла действия определяется по формуле

I g 0 = 2 па 0 .             (17)

Согласно формуле (16) интеграл дей- ствия в процессе спуска изменяется. В момент времени, когда кривая Ig (z) пересекает кривую интеграла действия, взятого на сепаратрисе, разделяющей вращательную и колебательную области, произойдет переход вращательного движения в колебательное.

Вычислим интеграл действия вдоль сепаратрисы. На с епаратрисе многочлен четвертой степени G(u) имеет два комплексных корня и два совпадающих действительных ( u34 ). Этот кратный корень должен одновременно удовлетворять условиям G(u34) = 0, GU (и34) = 0 • Этим условиям также удовлетворяет величина полной энергии h* . В результате преобразований интеграла (15), ис- a

пользуя подстановку u = tg у имеем следу-

ющее аналитическое выражение для интеграла действия, вычисленного вдоль сепаратрисы:

I g = Dz ,           (18)

где

D = | d 1 1 1 + d 2 1 2I + 1 3 ,         (19)

2 _ln 2 - -FP?

V X + 2 0 m + y m ² V r 2 — P 2        V У ² — P²

при p ² <  r ² ,

2              п        V У ^{2 + r 2}

,           ,—==--arctg—j^=^=

-j x + 2 0 m + Y m ² V P ² — r ^{2 2} V P ² — r ² при p ² >  r ² .

-^x + 20m + Ym2 P-^r2 - Pг arctg

y^P P^y ^{2 + r 2}

I 2

при p ² <  r ², 2

-У X + 2 0 m + Y m ² p 7 P 2 — r^г

ln(r)-Iny^P -rr2P±y + r-У2 + P2.

при P >  r •

I =   2(- ⁽u 34 ^{+ 1} ) ^ X ^{+ 2} ^ u 34 ⁺ T u 34

3"              (u 324 + 1),

Y—X± V ( Y—X ) 2 + 492 m, n =                        ,

2 = n2 +1 r 2 = X + 29 n + yn2 " m2 +1,      X + 29m + Ym m

n — u y =----- u34 — m ’

, V2 (m — n)d1 = —4——- (9 — X u 34 + Ym — 9 u 34 m), m2 +1

.   V2 (m — n)

d 2 =----2—;— (9 — X u 34 +Yn — 9 u 34 n), m2 +1

Y = h * — a о + b o , x = 3 x u з₄ — 4 c о u ₃₄ + 2 h * — 2 b ₀ ,

9 = Y u ₃₄ — c ₀ •

Приравнивая выражение для интеграла действия, описывающего его изменения в процессе спуска (16), выражению интеграла действия, вычисленного вдоль сепаратрисы (18), получим следующее уравнение для определения значения параметра z , при котором происходит переход вращательного движения в колебательное

A — Be ^{— C ( z — 1 )}= Dz .        (20)

Выражение для определения параметра z (20) упрощается, если демпфированием на начальном участке входа можно пренебречь. В этом случае изменение интеграла действия в процессе спуска определяется из соотношения (14) по формуле

2nL (z — 1 )

I g ⁽ z ) = I g 0 ⁺      _в----~ •      (21)

Тогда приравнивая выражение (21) к выражению для интеграла, вычисленного на сепаратрисе (18), и разрешая полученное уравнение относительно параметра z, получим z =

■! D

L2 ^{8 n}^ 0 f,   2^171 /f ^{4 n}^ 0

— „ D --1 I „ a-- r / 1 ------

4 p ( g ⁰    p JJ ( p

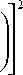
Зная величину z, при которой происходит переход вращательного движения в колебательное, и, учитывая, что z = exp(вt), можно определить значение времени перехода по формуле t = lnz/в •             (23)

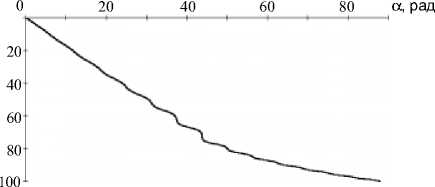
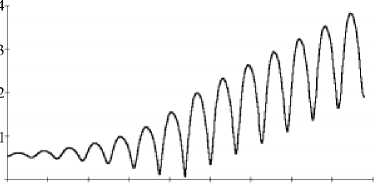
В случае, когда кривые (16) и (18) не пересекаются, переход вращательного движения в колебательное не происходит, возникает длительное вращение КА (плоская авторотация). На рис.5 показан случай такого движения (начальные условия движения:

a0 = —0,02 с"2, b0 = —0,005 с"2, c0 = —0,005 с"2, ^0 = 0,00087 с"2, о0 = —0,00001 с—1, a0 = 10 град,

(X₀ = 30 град/с , в = 0,05 с ^{— 1}).

Критическую угловую скорость ( a ₀ )_кр , задаваемую в разряженных слоях атмосферы, при превышении которой возникает плоская авторотация, можно определить из условия касания кривых (16) и (18) при выполнении (17). В этом случае критическая угловая скорость определяется по формуле

( a o ) p = [ a — { A — P/( 2 C) } e^{P 2 /( 4 D 2 C)} ] / ( 2 n ) , (24)

где P = AC — 7 A ² C ² — 2 CD ² .

В случае, если демпфированием можно пренебречь, выражение для критической угловой скорости принимает вид

( o ) „ = D = p / ( 16n² ^ 0 ) •        (25)

a, рад / с

t, с

Рис.5. Плоская авторотация

Следует отметить, что в отличие от аналогичных формул для критической угловой скорости, приведенных в [3] в интегральном виде, в формулах (24) и (25) параметр D выражен через элементарные функции (19). Формулы (24), (25) дают практически точный результат, когда справедливо уравнение для изменения интеграла действия (14), что соответствует большим значениям µ (условие (13)).

Таким образом, найдено решение для угла атаки в невозмущенном вращательном движении КА с малой асимметрией, аэродинамический момент которого описывается рядом Фурье по углу атаки с двумя первыми синусоидальными и первым косинусоидальным членами. Получено аналитическое выражение для интеграла действия, взятого вдоль сепаратрисы, разделяющей вращательную и колебательную области фазового портрета системы. Для возмущенного вращательного движения, обусловленного медленным изменением коэффициентов моментной характеристики, а также наличием и медленным изменением коэффициентов малой асимметрии и демпфирования, получены аналитические формулы для определения времен перехода вращательного движения в колебательное и критической угловой скорости внеатмосферного вращения, при превышении которой вращение аппарата продолжается в течение длительного интервала времени (возникает плоская авторотация).