Моделирование переходных процессов в системе генератор-трансформатор-нагрузка с несимметрией фазных контуров статора

Известно, что аналитическое исследование электромагнитных и электромеханических переходных процессов в синхронной машине с учетом всех влияющих факторов является весьма сложной задачей. В связи с этим для упрощения расчета приходится делать ряд допущений, которые вносят некоторые погрешности в оценку рассматриваемых параметров синхронной машины. Практическими методами расчета переходных процессов синхронной машины активно занимаются В.Ф. Сивокобыленко [1] (расчет синхронной машины при учете ротора машины многоконтурными схемами) и С.А. Харитонов [2] (описание электромагнитных переходных процессов в системах генерирования электрической энергии для автономных объектов). К основным допущениям, применяемым в таких методах расчета, можно отнести следующие:

• •    магнитная система машины не насыщена, в результате чего индуктивности машины не зависят от намагничивающей силы;

• •    вместо действительных кривых распределения магнитной индукции в воздушном зазоре по расточке статора учитываются только их составляющие первой гармоники;

• •    в магнитной системе машины отсутствуют какие-либо потери;

• •    считается, что конструкция машины обеспечивает полную симметрию фазных обмоток статора. Ротор также симметричен относительно своих продольной и поперечной осей [3].

Однако в некоторых случаях принятые при расчете допущения не позволяют выявить и провести корректный анализ ненормальных режимов синхронной машины. К такому режиму, например, можно отнести несимметрию фазных обмоток статора, вызванную наличием витковых замыканий в одной из них.

Существующие программные пакеты моделирования переходных процессов в электроэнергетических системах, такие как MATLAB Simulink [4], PSCAD, Mustang, используют для описания электромагнитных процессов синхронной машины уравнения Парка-Горева [3], которые записываются в неподвижной относительно ротора системе координат и предполагают полную симметрию фазных обмоток статора. Очевидно, что такой метод моделирования не может быть применен для расчета процессов в поврежденной синхронной машине с отличающимися параметрами фазных обмоток.

В исследуемой модели синхронной машины учитывают по одному продольному и поперечному демпферному контуру, пренебрегая влиянием эффекта вытеснения токов. В рамках же поставленных в исследовании задач допущение последнего не приведет к потере точности и недостоверным результатам.

В статье приведен вывод системы дифференциальных уравнений, описывающих переходные процессы трехфазной синхронной машины с учетом индивидуальных активных сопротивлений и индуктивностей обмоток. Далее произведено сравнение результатов моделирования переходных процессов в системе, выполненного посредством библиотеки блоков SimPowerSystems, входящей в состав среды MATLAB Simulink, с результатами, полученными с помощью предложенного метода.

Рассмотрим синхронную машину, имеющую три фазных обмотки, контур возбуждения, а также одну продольную и одну поперечную демпферные обмотки.

Обозначим через u _n (n = a, b, c ) и u f мгновенные значения напряжений на фазных обмотках и обмотке возбуждения соответственно; i _n и i f - мгновенные значения токов; y _n и у f — результирующие потокосцепления обмоток; R _η и R f – активные сопротивления фазных обмоток и обмотки возбуждения. Тогда дифференциальные уравнения равновесия э.д.с. и падений напряжений в контурах синхронной машины будут иметь вид [3]

u

d V dt

R n

( n = a, b, c );

dvf , _D • u_f =—— + кд.. f _dt ff

Кроме того, систему дифференциальных уравнений (1) следует дополнить уравнениями равновесия э.д.с. и падений напряжений в демпферных контурах:

0=

1

0 =

d V у d dt

- R у di- у d ;

-

d V у q

-

dt

^R у qⁱ у q ^,

где v yd и V yq — результирующие потокосцепления продольной и поперечной демпферных обмоток соответственно; R yd и R yq – их активные сопротивления; i yd и i yq – мгновенные значения токов в демпферных контурах.

Предлагаемый метод расчета переходных процессов основан на совместном решении уравнений (1) и (2), дополненных выражениями падений напряжений на сопротивлениях трансформатора и нагрузки. Такой подход делает возможным моделирование синхронной машины с различными параметрами фазных обмоток за счет описания электромагнитных процессов в каждой фазе отдельным дифференциальным уравнением.

Наиболее простая результирующая система дифференциальных уравнений пол е в случае подключения нагрузки по схеме «звезда» с нулевым проводом, не имеющим сопротивления [5]: достаточно выполнить замену u _п на i_Hrn ( di n / dt ) + R _нгn^zn ^в уравнении (1).

В действительности схемы выдачи мощности электростанций пр матривают работу генераторов с изолированной нейтралью (без нулевого провода). Как правило, генератор подключается к обмотке повышающего трансформатора, соединенной в «треугольник». Для точного расчета п так и тра                ,                                      .                                   . .

При расчете переходных процессов синхронной машины, работающей на автономную активно-индуктивную нагрузку, необходимо учесть следующие преобразования, в которых u_k ( k = ab, bc, ca ) - мгновенные значения линейных напряжений на выводах синхронной машины; i k – мгновенные значения линейных токов:

u ab	= и a	" u b ;	ie*	= i ab	- i ca ;
j u bc	= ub-	u „; * c	i b	= i	- i ab ;
u ca	= U c	u a ;	V	= i ca"	ibc

Тогда уравнения равновесия э.д.с. и падений напряжений в контурах синхронной машины в блоке с повышающим трансформатором (1) будут определяться как

[ “ •"■1	= ( L abT .1	di ab 1 + L 1 ) dt	- M bT . 1	Г., MbT . 1	diab 1	( R bng . 2 + R bT 2 ). "  ,             ib 2 L X b . 2		+ R abT1 i ab . 1 ;
				L X b . 2	dt
j u	( L bcT .1	di bc 1 + L ■ 1 ) dt	- McT 1 c	McT1	dibc 1	(R 2+ RtA " cng 2      cT 2 i c 2 L X c . 2
				L X c2	dt			bcT 1 bc 1 ;
U caTA	- ( T ( L caT .1	di ca 1 + L ■ л) dt	- M aT,	Г MaT .1	dica 1	C R 2+ Rr2) ang 2      aT 2 .             ia 2 L X a . 2		+ 1 ccaT .1 i ca . 1 ’
				L X a.	dt

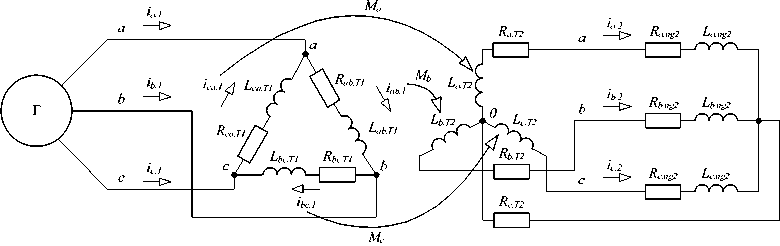
Рис. 1. Схема подключения нагрузки Fig.

где L_{kT .1} , L_{k σ T .1} ( k = ab , bc , ca ) – собственное значение индуктивности первичной обмотки трансформатора, обусловленное основным магнитным потоком и потоком рассеяния соответственно; M _n T (n = a, b, c ) — взаимная индуктивность обмоток трансформатора; L^ 2 = L _n ng 2 + L ^ T 2 + L ^ T 2 -суммарное значение индуктивностей на вторичной стороне системы; R η ng .2 – активное сопротивление нагрузки; R_{kT .1} , R _{η T .2} – активное сопротивление первичной и вторичной обмотки трансформатора; u kT .1 – мгновенные значения линейных напряжений на первичной обмотке трансформатора, ψ _ij = ψ _i – ψ _j .

Обращаясь к описанию электромагнитных процессов синхронной машины уравнения Парка–Горева, которые записывают в неподвижной относительно ротора системе координат, видис, что продольное синхрон ное индукти вное сопр от ивление не является постоянным, а зависит от насыщения машины. Эта зависимость приближенно может быть выявлена с помощью характеристики х.х. машины. Подробно определение влияния насыщения магнитной системы на величину синхронного инд укт ивного с опро т ивл ен ия изложено в [6], где рассмотрено построение характеристики х.х. и выведены все необходимые величины. В данном исследовании насыщение магнитной системы как синхрон ной маш ин ы, так и пов ышающего трансформатора не учитывается.

Стоит отметить, что в исследовании учтены только взаимные индуктивности между первичной и вторичной обмотками трансформатора. Взаимные индуктивности между фазами не принимают во внимание. Таким образом, модель можно представить в виде группы однофазных трансформаторов.

При расчете переходных процессов синхронной машины, работающей на автономную активно-индуктивную нагрузку, дифференциальные уравнения принимают вид

dt  =  uabT.1   [(Rg.a + Rg.b ) iab   Rg.a^ca   Rg.bibc ] ; dt  =  ubcTл   [(Rg b + Rg c) ibc   Rg.biab   Rg.cica ] ; — UCQT 1 ГСRg c+ Rg Q ) ica Rg cibc Rg iab ] ; caT .1          g .c      g.a ca      g.c bc      g.a ab dt                                                                                 (4) dd f -ЦТ ~ uf-Rflf; ddУd           . dt      R l уd • ddtq. = _R , dt          уqyq ’ где Кд.л (n = a, b, с) - активное сопротивление контура фазной обмотки генератора.

Для упрощения восприятия условно примем замену переменных, где L k ₂ ( k = ab , be , са ) -суммарные собственные индуктивности контуров; M k . e - эквивалентные взаимные индуктивности контуров; u Σ k – мгновенные значения падений напряжения на активных сопротивлениях контуров:

L . = L + L - 2 M . + L . _т . + L .   + —— ;

ab L a b          ab abT .1       abd .1 г ’

L z b .2

L bc L = L b + L c - 2 M bc + L bcT .1 + L bcdTl + /; L z c .2

L ca L = L c + L a - 2 M ca + кг _Л + L cadT1 + , ;

L z a. 2

M ab . e = M bc + M ab - M ca - L b ; M bc . e = M bc + M ca - M ab - L c ; . M ca . e = M ca + M ab - M bc - L a ;

u z ab = - ^MbT .1

( R bng .2 + R bT2 ).

ib

^L z b .2

( R ,+ R_T ,)

j u z bc = - M cT л      ,---- i c .2 - ( R g . b + R g . c + R bc . 1 ) i bc + R gkb + R g . jca ;

^{L z} c"

u z ca = - M aT Л   R ang 2 ^{+ R}a^{T 2} ) i a 2 - ( R g . c + R g . a + R ca Л ) i ca + R g . c i bc + R g . a^ab-

^L z a .2

Коэффициенты пропорциональности L_a, L b , L_e, Lf- , L yd , L yq есть собственные индуктивности фазных обмоток, обмотки возбуждения, продольной и поперечной демпферных обмоток соответственно, символом M обозначены взаимные индуктивности обмоток. Как определяются эти коэффициенты, подробно раскрыто в [3], и останавливаться на их рассмотрении не имеет смысла. Стоит лишь отметить, что большинство индуктивностей, входящих в выражение (5), являются функциями угла поворота ротора γ. При нарушении симметрии фазных контуров статора эти индуктивности могут быть определены с помощью дополнительного коэффициента, учитывающего долю замкнувшихся витков k w _л (n = а, b, с ).

Решение системы уравнений (1) включает в себя определение производной d ш k / dt от сложной функции, зависящей от токов в контурах и угла поворота ротора. Для этого к системе (2) применим формулу производной сложной функции

Nk, dt

Sy dt ^ 8i_m dt

( k , m = ab , bc , ca , f , у d , у q )

и подставим полученные выражения в (1). Так как процесс определения производных для разных контуров однотипен, рассмотрим лишь одно уравнение для контура “ ab” статора:

Nab dt

Y dt " *'   dt “' dt   "' ' "f bf ¹ dt

+ (Mayd — Mbyd )    + (Mayq — Mbyq ) d^ = — Lnab ^ — U dt                  dt          dt

Уравнения для остальных контуров могут быть получены тем же способом.

Частную производную потокосцепления по углу, входящую в (6), выразим следующим образом:

d^ab = dLabe i + dM obe i + dM„ i + d (M af — M bf ) i + dy     dy ab dy bc    dy ca        dy      f                   (7)

₊ d ( M ayd — M byd ) _z , d ( M ayq — M byq ) _;

d y         у^d           d y         у q'

Выведенные в (6) производные индуктивностей по углу можно определить, зная исходные выражения индуктивностей, полученные в [3].

В результате подстановки (7) в (6) получим уравнение, связывающее функции времени – токи в обмотках и угол поворота ротора – и производные этих функций.

При рассмотрении всех контуров синхронной машины вместо одного уравнения (6) получим следующую систему уравнений в матричном виде:

Lab Z M ab e Mca e Mabf M abуd Mabуq " " diab/dt" Г  -(bVaJ b, )Ш + u E ab  1 Mabe Lbc X Mbc e Mbcf M bcуd Mbcуq dibc/dt -(dVbc I^Y)® + u У be Mcae Mabf Mbc e Mbcf Lca Z Mcaf MLcaf Mcaуd Mfуd M caуq 0 ■ dica/dt dif/dt = -(6Vca/SY )Ш + u , ea цву f /Sy )®—Rfif+Uf , (8) Mab уd Mbcуd Mcaуd M ffуd Lуd 0 di уd/dt -(av „ yY)®—R,d,„ _ Mab уq Mbcуq Mcaуq 0 0 L у q _ _ di уq/dt _ [ —W y q   )Я — R у qi, j где Mkf, Mkyd, Mkyq (k = ab, bc, ca) - значения взаимной индуктивности обмотки возбуждения, продольной и поперечной демпферных обмоток.

Помимо системы (8), необходимо определить значения токов во вторичной обмотке транс -форматора, для чего воспользуемся системой уравнений:

di a. _ Mt .1 dica.1 (r , + rtA \ ang.2 aT.2 / dt L1 a .2 dt L1 a .2 dib -2 _ MbT.1 diab.1 (Rbng2 + RbT.2 ) dt L1 b .2 dt L1 b2 di c. _ McT.1 dibc.1 ( Rcng2 + RcT2 ) dt Lvc2 1 c .2 dt L1 c2 ib .2;

i c .2^.

i a .2 ;

Полученная система уравнений (8) позволяет определять производные токов в обмотках по известным значениям функций (токов, угла поворота ротора и частоты).

Для описания электромеханических процессов синхронной машины применим дифференциальное уравнение движения ротора в форме д’Аламбера [3]:

„ - / .    W = о ,

т dt    dY , где MT - момент турбины; J- момент инерции ротора; WM - энергия магнитных полей машины, которая может быть определена по формуле [3]:

^W m = 1 Е i k V k ^{, k} = a ^{, b ,} c ^, f ,у ,y q ■

2k

При подстановке (10) в (9) и преобразований получим следующее выражение для расчета производной частоты по известным значениям функций:

d ® _ P m , ¹ L ^dV a ,   ^dV b ,   ^dV c ,   ^aV f

—1 i a и i b и i c и i f и i у d dt   J га 2 J I dy dy dy d Qy У

'■

Sy

⁺ i у q

^dW у q di

где P – мощность турбины. Частные производные потокосцеплений по углу, полученные в (11), входят также в систему уравнений (8), и их определение уже рассмотрено ранее.

Для получения полной системы дифференциальных уравнений, описывающих переходные процессы синхронной машины, необходимо (8) и (11) дополнить связью между угловой частотой и углом поворота ротора:

dу

— — to.

dt

Численное решение системы обыкновенных дифференциальных уравнений (разностными методами) требует расчета производных функций по известным значениям самих функций на каждом шаге интегрирования [7]. Для этого система обычно представляется в форме Коши. В рассматриваемом случае два уравнения (11) и (12) содержат по одной производной в левой части, в то время как оставшиеся уравнения заданы в матричном виде (9), причем разделение переменных затруднительно из-за большого порядка матриц.

Кроме того, указанные уравнения имеют переменные коэффициенты, зависящие от угла поворота ротора γ. В итоге требуется пересчет большинства коэффициентов на каждом шаге – 946 – интегрирования, и представление (8) в явной форме Коши не обеспечило бы существенного снижения объема вычислений.

Предложенная математическая модель синхронного генератора реализована при помощи программного пакета MATLAB. Данная программа широко применяется в различного рода исследованиях переходных процессов в синхронных и асинхронных машинах [8-11]. Для решения системы дифференциальных уравнений использована функция ode45, основанная на одношаговом явном методе Рунге-Кутта 4-го и 5-го порядка [4]. За основу метода расчета производных при численном решении системы дифференциальных уравнений взят алгоритм, предложенный в [5].

Однако не всегда применение пакета MATLAB отвечает требуемому быстродействию. Для повышения скорости вычислений авторы [5, 12] предлагают методы дополнительной оптимизации программного кода.

В качестве примера для сравнения моделей выполнены расчеты переходных процессов генератора ТВВ-200-2AУ3 с полной симметрией фазных обмоток статора и следующими параметрами: S ,ом = 235.3 MB • A, U „„ = 15.57 кВ, f _юм = 50 Гц, X d = 2.106, x'_d = 0,272, x d = 0,1805, x q = 2.106, x q = 0.1805, x „ = 0.166, T = 0.91 c, T d = 0.114 c, Tq" = 0.114 c, активное сопротивление обмотки статора R s = 0.00152 Ом. Трансформатор ТДЦ-250000/110 имеет параметры: S номT = 250 MB · A, U номBH = 121 кB, U номHH = 15.75 кB, U k = 10.5 %, P k = 640 кВт, I k = 0.5 %.

Работа системы рассматривается в нескольких режимах: в нормальном установившемся режиме под нагрузкой, подача напряжения на обмотку возбуждения при отключенной нагрузке.

Результаты расчетов в нормальном установившемся режиме под нагрузкой с помощью моделирования численным методом и в среде MATLAB Simulink приведены на рис. 2 и 3.

Из сравнения полученных результатов нормального установившегося режима работы генератора можно увидеть, что при численном методе моделирования имеем следующее: амплитуд-

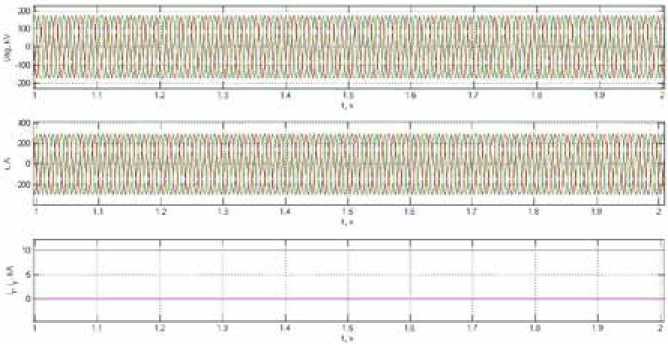
Рис. 2. Результаты расчетов численным методом моделирования в нормальном установившемся режиме под нагрузкой

Fig. 2. The results of calculations by the numerical simulation method in the normal steady state under load

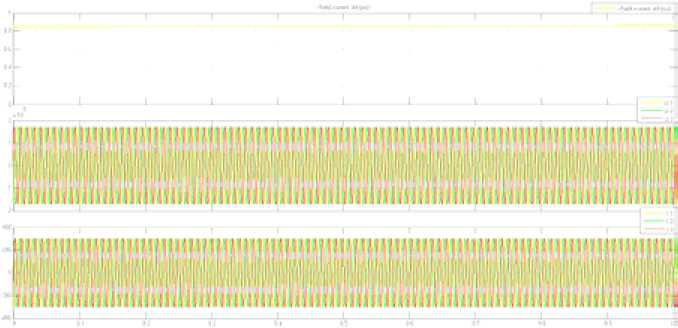
Рис. 3. Результаты расчетов в среде Simulink в нормальном установившемся режиме под нагрузкой

Fig. 3. Results of Simulink calculations in the normal steady state under load ное значение напряжения на вторичной обмотке трансформатора – составляет uabT.2 = 172.7 кВ, амплитудное значение фазного тока вторичной обмотки трансформатора ia.2 = 294 A. При моделировании генератора в среде MATLAB Simulink эти значения составляют uabT.2 = 176.1 кВ, ia.2 = 302 A соответственно.

Результаты расчетов при подаче напряжения на обмотку возбуждения и отключенной нагрузке с помощью моделирования численным методом и в среде Simulink приведены на рис. 4 и 5.

Сравнение полученных результатов режима холостого хода генератора показывает, что при численном методе моделирования амплитудное значение э.д.с. контуров статора составляет u_{abT .2} = 173.1 кВ. При моделировании генератора в среде MATLAB Simulink u_{abT .2} = 175.2 кВ.

Рис. 4. Результаты расчетов численным методом моделирования при подаче напряжения на обмотку возбуждения и отключенной нагрузке

• Fig. 4.    The results of calculations by a numerical simulation method with a voltage applied to the excitation winding and the disconnected load

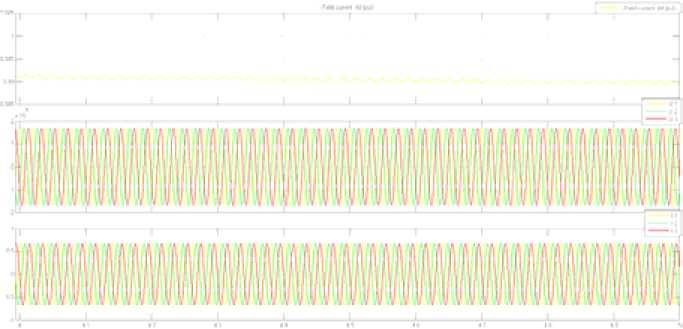
Рис. 5. Результаты расчетов в среде Simulink при подаче напряжения на обмотку возбуждения и отключенной нагрузке

• Fig. 5.    Results of calculations in the Simulink environment when applying voltage to the excitation winding and the disconnected load

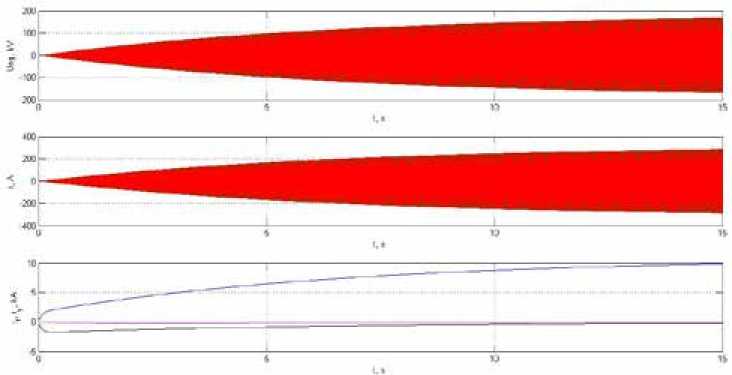
Рис. 6. Результаты расчетов численным методом моделирования переходного процесса в синхронной машине

• Fig. 6.    Results of numerical simulation of the transient process in a synchronous machine

На рис. 6 представлены результаты численного моделирования переходного процесса в синхронной машине при выходе ее на нормальный установившийся режим работы.

Полученные в ходе исследования результаты сравнения расчетного метода и модели в среде MATLAB Simulink при работе с симметричными фазными контурами статора и без учета насыщения магнитной системы показали достоверность предлагаемого численного метода моделирования.

Реализованная математическая модель дает возможность рассматривать влияние несим-метрии фазных контуров статора и насыщения магнитной системы при моделировании синхронной машины.

В перспективе предлагаемый метод позволит использовать результаты расчетов переходных процессов синхронной машины для анализа работы и создания новых алгоритмов релейной защиты генераторов электростанций.

• [1]    Сивокобыленко В.Ф. Математическое моделирование синхронной машины с многоконтурным ротором в фазных координатах. ISSN 1607-7970 . Техническая электродинамика , 2015, 1, 51–58 [Sivokobyilenko V.F. Mathematical modeling of a synchronous machine with a multi-loop rotor in phase coordinates. ISSN 1607-7970. Technical electrodynamics , 2015, 1, 51–58 (in Russian)]

• [2]    Харитонов С.А. Электромагнитные переходные процессы в системах генерирования электрической энергии для автономных объектов . Новосибирск: Изд-во НГТУ, 2011. 536 с. [Haritonov S.A. Processes in Power Generating Systems for Stand-Alone Units . Novosibirsk, NSTU, 2011. 536 p. (in Russian)]

• [3]    Горев А.А. Переходные процессы синхронной машины . Л.: Наука, 1985. 502 с. [Gorev A.A. Transient processes of a synchronous machine . L., Science, 1985. 502 p. (in Russian)]

• [4]    Черных И.В. Моделирование электротехнических устройств в MATLAB. SimPowerSystems и Simulink . М.: ДМК Пресс, 2008. 288 с. [Chernyih I.V. Modeling of electrical devices in MATLAB. SimPowerSystems and Simulink. M., HMC Press , 2008. 288 p. (in Russian)]

• [5]    Глазырин Г.В. Моделирование переходных процессов синхронной машины с несим-метрией фазных обмоток статора. Вестник МЭИ , 2017, 5, 34–39 [Glazyirin G.V. Simulation of transient processes of a synchronous machine with the asymmetry of phase stator windings. Newsletter MEI , 2017, 5, 34–39 (in Russian)]

• [6]    Жданов П.С. Вопросы устойчивости электрических систем . М.: Энергия, 1979. 456 с. [Zhdanov P.S. Questions of the stability of electrical systems . M., Energy, 1979. 456 p. (in Russian)]

• [7]    Мэтьюз Д.Г., Финк К.Д. Численные методы. Использование MATLAB, 3-е изд : Пер. с англ . М.: Издательский дом «Вильямс», 2001. 720 с. [Mathews D.G., Finck K.D. Numerical methods. Using MATLAB , 3rd edition. M., Publishing house «Williams», 2001. 720 p. (in Russian)]

• [8]    Файзиев М.М., Курбонов Н.А., Имамназаров А.Б., Бекишев А.Э. Моделирование пуска асинхронных двигателей в МАTLAB. Вестник науки и образования , 2017, 3(27), 4247 [Fayziev M.M., Kurbonov N.A., Imamnazarov A.B., Bekishev A.E. Modeling of start-up of asynchronous motors in МАTLAB, Bulletin of Science and Education , 2017, 3(27), 42-47 (in Russian)]

• [9]    Субботина В.А., Тюленев М.Е. Simulink – модель для исследования пуска синхронного двигателя при пониженном напряжении. Электротехника, информационные технологии, системы управления , 2014, 11, 102–109 [Subbotina V.A., Tyulenev M.E. Simulink is a model for investigating the start-up of a synchronous motor under reduced voltage. Electrical engineering, information technology, control systems , 2014, 11, 102-109 (in Russian)]

• [10]    Федий К.С., Встовский С.А., Полошков Н.Е. Моделирование переходных процессов в торцевом синхронном генераторе в пакете MATLAB. Журнал Сибирского федерального университета. Техника и технологии , 2017, 10(5), 691–698 [Fediy K.S., Vstovsky S.A., Poloshkov N.E.

Simulation of transients in the face synchronous generator in the MATLAB package, Journal of Siberian Federal University. Engineering and technology , 2017, 10(5), 691-698 (in Russian)]

• [11]    Demiroren A. and Zeynelgil H.L. Modelling and simulation of synchronous machine transient analysis using SIMULINK. International Journal of Electrical Engineering Education , 2002, 39/4, 337–346.

• [12]    Hafnaoui I., Ayari R., Nicolescu G., Beltrame G. A simulation-based model generator for software performance estimation. SCSC ’16 Proceedings of the Summer Computer Simulation Conference . USA, 2016, ISBN: 978-1-5108-2424-9.