Моделирование переходных процессов в торцевом синхронном генераторе в пакете MATLAB

– в системе координат, жестко связанной с ротором.

Для удобства расчета выберем вариант с неподвижной системой координат относительно ротора машины.

Таким образом, выражая переменные, описывающие характер протекания процессов и характеризующие свойства машины (потокосцепление, ток и напряжения в каждой фазе трехфазной системы) через новые коэффициенты, привязанные к какой-либо системе координат, избавляются от периодических коэффициентов дифференциальных уравнений синхронной машины.

Особенностью математической модели торцевого синхронного генератора с магнитоэлектрическим возбуждением является замена постоянных магнитов на «фиктивную» обмотку возбуждения с включенным в неё источником тока I 'В = const , равным МДС «фиктивной» коэрцитивной силы ^ мф = Н сф ■ l м .

Библиотека блоков SimPowerSystems выступает одной из множества дополнительных библиотек Simulink пакета MatLab, ориентированных на моделирование конкретных устройств. Несомненным достоинством SimPowerSystems признано то, что сложные электротехнические системы можно моделировать, сочетая методы имитационного и структурного моделирования. Например, силовую часть полупроводникового преобразователя электрической энергии можно выполнить с использованием имитационных блоков SimPowerSystems, а систему управления – с помощью обычных блоков Simulink, отражающих лишь алгоритм ее работы, а не ее электрическую схему. Такой подход в отличие от пакетов схемотехнического моделирования позволяет значительно упростить всю модель, а значит, повысить ее работоспособность и скорость работы. Кроме того, в модели с использованием блоков SimPowerSystems (далее SPS-модели) можно применять блоки и остальных библиотек Simulink, а также функции самого MatLab, что дает практически неограниченные возможности для моделирования электротехнических систем.

На рис. 1 представлена схема модели генератора с постоянными магнитами, реализованная при помощи пакета MatLab в Simulink. Особенность схемы заключается в том, что она

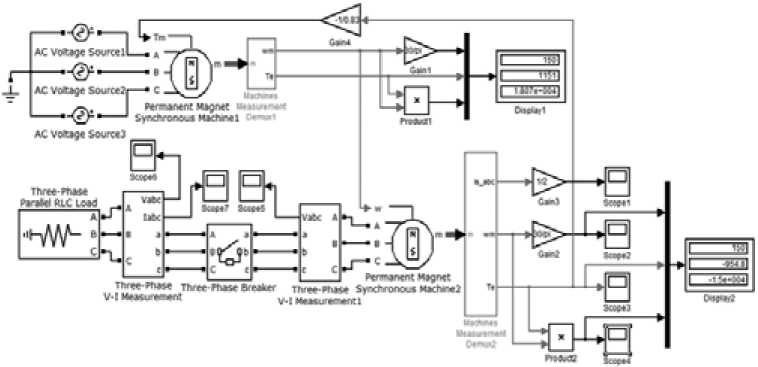
Рис. 1. Модель генератор-двигатель позволяет посмотреть переходные процессы сразу как в двигательном, так и в генераторном режиме.

При реализации модели возникает проблема задания частоты вращения привода генератора из-за отсутствия в библиотеке Simulink стандартных двигателей с малой частотой вращения ротора. Эта проблема решается использованием двух одинаковых синхронных машин с постоянными магнитами характеристики, которых рассчитаны с помощью разработанной математической модели. Выходная мощность двигателя, необходимая для вращения генератора, рассчитывается по формуле

^Рд = — ,                                                   (1)

Пг где Рг – мощность генератора, кВт; ηг – КПД генератора, о.е.

Так, например, для генератора мощностью 15 кВт требуется приводной двигатель мощностью Р _д = 15/0,83 = 18,07 кВт.

Основной элемент модели – блок Permanent Magnet Synchronous Machine, являющийся моделью синхронной машины с постоянными магнитами из электротехнической библиотеки SimPowerSystems (рис. 2).

Порты модели A, B и С – выводы статорной обмотки машины. Входной порт Tm служит для задания механического момента. На выходном порту m формируется векторный сигнал, состоящий из 10 элементов:

• -    1-3: токи обмотки статора - i sa , i sb , i sc ;

• -    4-5: проекции токов статора на оси d и d - i d , i q ;

• -    6-7: проекции напряжений статора на оси d и d - U_d, U q ;

• –    8: угловая частота вращения ротора – ω r ;

• –    9: угол поворота ротора – θ;

• ^-    1^0: электромагнитный момент ^- T e .

Для удобства извлечения переменных машины из выходного вектора измеряемых переменных в библиотеке SimPowerSystems предусмотрен блок Machines Measurement Demux.

Электрическая часть модели машины описывается системой уравнений, связанных с ротором [1]:

d 1 ⋅ i = dt ^d L d

RL

• ■    Ud -    ■ id + ^ ■ p ■ ® r ■ iq

Ld      Ld

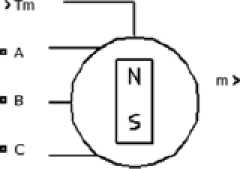
Рис. 2. Блок Permanent Magnet Synchronous Machine

d

⋅ i_q dt

= 1 ⋅ U	R	L	λ⋅ p ⋅ω r
	—	⋅ i + d ⋅ p ⋅ω ⋅ i
q q	L q	qL     rd q	L q

T e = 1,5 ⋅ p ⋅ ( λ⋅ i d + ( L d - L q ) ⋅ i d ⋅ i q .

Все параметры ротора и его переменные приведены к статору. В системе уравнений приняты следующие обозначения:

• -    L d , L q - индуктивности статора по осям d и d ;

• -    R - активное сопротивление обмотки статора;

• –    λ – магнитный поток постоянных магнитов, сцепленный с обмоткой статора.

Механическая часть модели описывается уравнениями:

d 1

T m ),

⋅ ωr =   ⋅ (Te - F ⋅ ωr - dt J

d •9 = ”r,                                                                 (6)

dt где J - суммарный момент инерции ротора и нагрузки; F - коэффициент трения; 9 - угол положения ротора; Tm - момент сопротивления.

Процессы, возникающие в синхронных машинах при переходных режимах, например при внезапном коротком замыкании или резком изменении нагрузки, весьма сложны, что вызывает значительные трудности при их точном количественном расчете [2]. Однако поведение синхронной машины при указанных режимах имеет очень большое практическое значение, так как переходные процессы могут вызвать повреждение машины, а следовательно, и значительные убытки, связанные с перерывом энергоснабжения объектов, получающих питание от генератора, или прекращением работы электроприводов с синхронными двигателями [3].

На рис. 3 и 4 представлены переходные процессы, происходящие в обмотке статора ТСГ на постоянных магнитах.

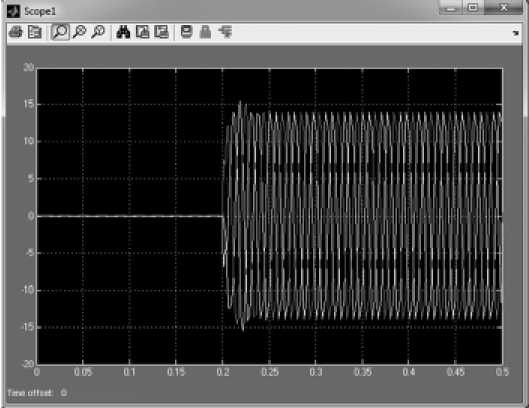
Рис. 3. График токов обмотки статора генератора

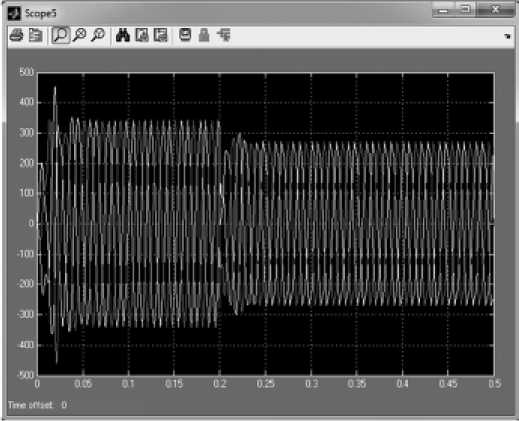
Рис. 4. График напряжений обмотки статора генератора

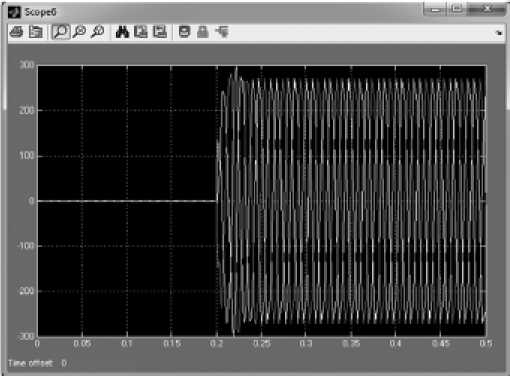
Рис. 5. График напряжений на номинальной нагрузке

В момент времени 0 с происходит пуск генератора, при этом появляются скачки напряжения. В период времени с 0,05 до 0,2 с генератор работает в установившемся режиме холостого хода. В момент времени 0,2 с происходит замыкание ключа и к генератору подводится активная нагрузка, при этом появляются скачки тока (рис. 3) и падение напряжения в обмотке статора (рис. 4). С момента времени 0,25 с генератор работает уже в установившемся режиме работы на номинальную нагрузку (рис. 5).

На рис. 6-8 видно, что в начальный момент короткого замыкания (0,2 с) машина испытывает сильный удар за счет резко возросших токов статорной обмотки и кинетической энергии ротора. В результате этого возникает тормозящий момент, имеющий характер кратковременного импульса, во время которого скорость машины падает до 60 об/мин, поэтому необходимо – 696 –

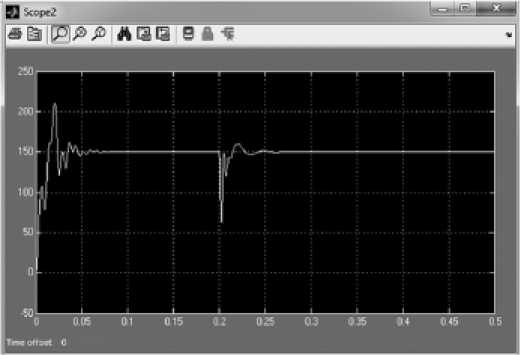
Рис. 6. График частоты вращения ротора

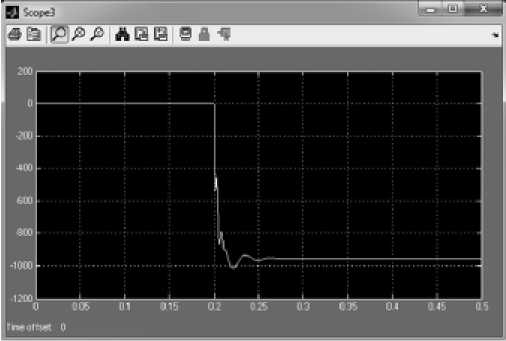
Рис. 7. График электромагнитного момента

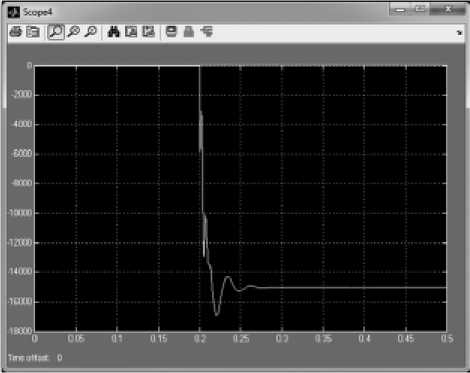
уделять большое внимание обеспечению механической прочности машины, прежде всего ее активной части.

Графическое значение номинального тока обмотки статора составляет 13.9 А, что очень близко к расчетному значению номинального тока 14.2 А. Расхождение результатов моделирования и результатов аналитического расчета незначительно, что позволяет предположить правильность построения имитационной модели ТСГ на постоянных магнитах и задания параметров моделирования.

Исследование переходных процессов при внезапном трехфазном коротком замыкании рассматривались для исследования величин токов, возникающих при коротком замыкании, и определения динамических сил, возникающих вследствие взаимодействия токов короткого замыкания и магнитных полей.

Определение величин токов короткого замыкания и их изменения во времени в первую очередь особо важно для конструкторов электрических сетей и распределительных устройств, так как динамическая нагрузка устройств определяется максимальным значением тока короткого замыкания, а изменение токов короткого замыкания во времени имеет решающее значение при выборе выключателей.

Проведенные исследования показали, что вид графиков при внезапном трехфазном коротком замыкании практически идентичен полученным графикам переходных процессов при сбросе и набросе нагрузки, что связано с тем, что постоянные магниты имеют малую магнитную проницаемость (ц~1,5 - 4 Цо)-